portion of a raster cell covered by one or more polygons: is there a faster way to do this (in R)?

Question

Pictures are better than words, so please have a look at

What I have is

• a RasterLayer object (filled with random values here for illustration purposes only, the actual values don't matter)
• a SpatialPolygons object with lots and lots of polygons in it

You can re-create the example data I used for the image with the following code:

library(sp)
library(raster)
library(rgeos)

# create example raster
r <- raster(nrows=10, ncol=15, xmn=0, ymn=0)
values(r) <- sample(x=1:1000, size=150)

# create example (Spatial) Polygons
p1 <- Polygon(coords=matrix(c(50, 100, 100, 50, 50, 15, 15, 35, 35, 15), nrow=5, ncol=2), hole=FALSE)
p2 <- Polygon(coords=matrix(c(77, 123, 111, 77, 43, 57, 66, 43), nrow=4, ncol=2), hole=FALSE)
p3 <- Polygon(coords=matrix(c(110, 125, 125, 110, 67, 75, 80, 67), nrow=4, ncol=2), hole=FALSE)

lots.of.polygons <- SpatialPolygons(list(Polygons(list(p1, p2, p3), 1)))
crs(lots.of.polygons) <- crs(r) # copy crs from raster to polygons (please ignore any potential problems related to projections etc. for now)


# plot both
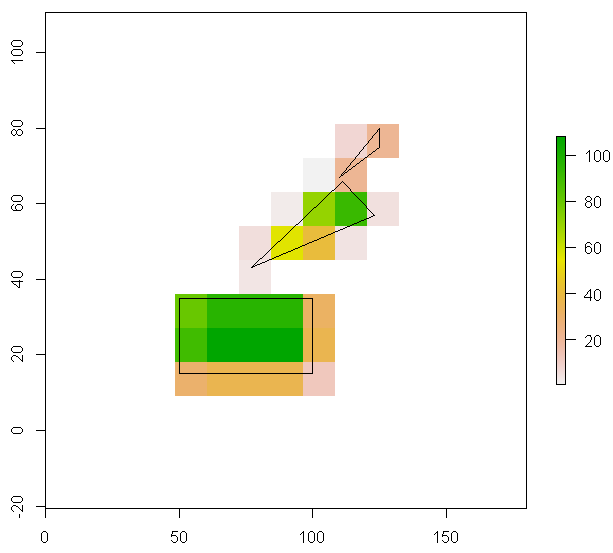
plot(r) #values in this raster for illustration purposes only
plot(lots.of.polygons, add=TRUE)

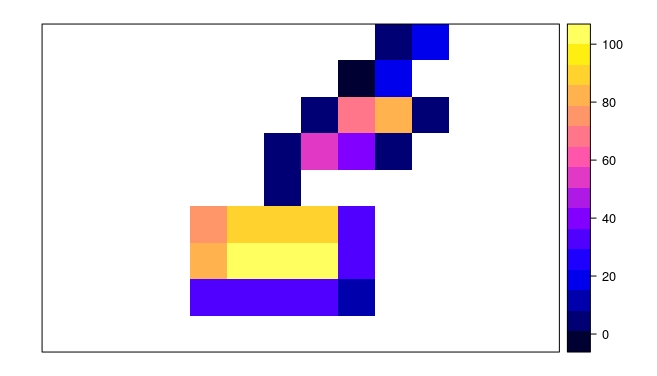
For each cell in the raster, I want to know how much of it is covered by one or more polygons. Or actually: the area of all polygons within the raster cell, without what is outside the cell in question. If there are multiple polygons overlapping a cell, I only need their combined area.

The following code does what I want, but takes more than a week to run with the actual data sets:

# empty the example raster (don't need the values):
values(r) <- NA

# copy of r that will hold the results
r.results <- r

for (i in 1:ncell(r)){
  r.cell <- r # fresh copy of the empty raster
  r.cell[i] <- 1 # set the ith cell to 1
  p <- rasterToPolygons(r.cell) # create a polygon that represents the i-th raster cell
  cropped.polygons <- gIntersection(p, lots.of.polygons) # intersection of i-th raster cell and all SpatialPolygons

  if (is.null(cropped.polygons)) {
    r.results[i] <- NA # if there's no polygon intersecting this raster cell, just return NA ...
  } else{
    r.results[i] <- gArea(cropped.polygons) # ... otherwise return the area
  }
}

plot(r.results)
plot(lots.of.polygons, add=TRUE)

I can squeeze out a bit more speed by using sapply instead of the for-loop, but the bottleneck seems to be somewhere else. The whole approach feels pretty awkward, and I'm wondering if I've missed something obvious. At first I thought rasterize() should be able to do this easily, but I can't figure out what to put into the fun= argument. Any ideas?

Janeanjaneczka

Be aware that [For polygons, values are transferred if the polygon covers the center of a raster cell. ](cran.rstudio.com/web/packages/raster/raster.pdf). You could use foreach loops to use your multiple cores (if available). – Respectability

Answer 1

[edited]

Maybe gIntersection(..., byid = T) with gUnaryUnion(lots.of.polygons) (they enable you to treat all cells at once) is faster than for loop (If gUnaryUnion() takes too much time, this is a bad idea).

r <- raster(nrows=10, ncol=15, xmn=0, ymn=0)
set.seed(1); values(r) <- sample(x=1:1000, size=150)
rr <- rasterToPolygons(r)

# joining intersecting polys and put all polys into single SpatialPolygons
lots.of.polygons <- gUnaryUnion(lots.of.polygons)   # in this example, it is unnecessary

gi <- gIntersection(rr, lots.of.polygons, byid = T)

ind <- as.numeric(do.call(rbind, strsplit(names(gi), " "))[,1])   # getting intersected rr's id
r[] <- NA
r[ind] <- sapply(gi@polygons, function(x) slot(x, 'area'))  # a bit faster than gArea(gi, byid = T)

plot(r)
plot(lots.of.polygons, add=TRUE)

Olag

since the question is how to speed things up, it would probably be nice to microbenchmark the approaches. – Respectability

Great answer, thanks a lot. I did microbenchmark it and it seems to be faster than my original solution by nearly an order of magnitude (at least for the example data set). – Indonesia

Also consider that you exclude all pixels from this evaluation which are not at all covered by the polygons beforehand to speed up calculations. Yet, you have to keep in mind that you find a proper way to work around the problem that e.g. mask will only respect cells which have their centroid within the polygons! – Respectability

@loki; Thanks again for your support !! – Olag

Answer 2

you can parallelize your loop using the doSNOW and foreach packages. This would speed up the calculations by the by the number of your CPUs

library(doSNOW)
library(foreach)

cl <- makeCluster(4) 
# 4 is the number of CPUs used. You can change that according 
# to the number of processors you have 
registerDoSNOW(cl)

values(r.results) <- foreach(i = 1:ncell(r), .packages = c("raster", "sp", "rgeos"), .combine = c) %dopar% {
  r.cell <- r # fresh copy of the empty raster
  r.cell[i] <- 1 # set the ith cell to 1
  p <- rasterToPolygons(r.cell) # create a polygon that represents the i-th raster cell
  cropped.polygons <- gIntersection(p, lots.of.polygons) # intersection of i-th raster cell and all SpatialPolygons

  if (is.null(cropped.polygons)) {
    NA # if there's no polygon intersecting this raster cell, just return NA ...
  } else{
    gArea(cropped.polygons) # ... otherwise return the area
  }
}

plot(r.results)
plot(lots.of.polygons, add=TRUE)

Respectability

Thanks for the idea, I hadn't even thought about parallelizing. Seems to work for me, so I'll try to combine that with cuttlefish44's solution. – Indonesia

You should note, that foreach loops generate a bigger overhead than for loops, since all used packages and objects have to be loaded into the individual workers. Therefore, the power of foreach will be more noticeable with a bigger data set. – Respectability

Answer 3

As you mentioned in your question, an alternative could be to exploit rasterization to speed up things. This would involve creating two raster files: one "fishnet" raster with values corresponding to the cell numbers, and one with values corresponding to the IDs of the polygons. Both need to be "resampled " to a larger resolution than that of the original raster of the cells. Then you can count how many of the cells of the supersampled fishnet with the same cell number correspond to cells of the polygons raster with a valid (non-zero) id. In practice, something like this would work (Note that I slightly changed the building of the input polygons to have a SpatialPolygonsDataFrame.

library(sp)
library(raster)
library(rgeos)
library(data.table)
library(gdalUtils)

# create example raster
r <- raster(nrows=10, ncol=15, xmn=0, ymn=0)
values(r) <- sample(x=1:1000, size=150)

# create example (Spatial) Polygons --> Note that I changed it slightly
# to have a SpatialPolygonsDataFrame with IDs for the different polys

p1 <- Polygons(list(Polygon(coords=matrix(c(50, 100, 100, 50, 50, 15, 15, 35, 35, 15), nrow=5, ncol=2), hole=FALSE)), "1")
p2 <- Polygons(list(Polygon(coords=matrix(c(77, 123, 111, 77, 43, 57, 66, 43),         nrow=4, ncol=2), hole=FALSE)), "2")
p3 <- Polygons(list(Polygon(coords=matrix(c(110, 125, 125, 110, 67, 75, 80, 67),       nrow=4, ncol=2), hole=FALSE)), "3")
lots.of.polygons <- SpatialPolygons(list(p1, p2, p3), 1:3)
lots.of.polygons <- SpatialPolygonsDataFrame(lots.of.polygons, data = data.frame (id = c(1,2,3)))
crs(lots.of.polygons) <- crs(r) # copy crs from raster to polygons (please ignore any potential problems related to projections etc. for now)

# plot both
plot(r) #values in this raster for illustration purposes only
plot(lots.of.polygons, add = TRUE)


# Create a spatial grid dataframe and convert it to a "raster fishnet"
# Consider also that creating a SpatialGridDataFrame could be faster
# than using "rasterToPolygons" in your original approach !

cs <- res(r) # cell size.
cc <- c(extent(r)@xmin,extent(r)@ymin) + (cs/2)   # corner of the grid.
cd <- ceiling(c(((extent(r)@xmax - extent(r)@xmin)/cs[1]), # construct grid topology
                ((extent(r)@ymax - extent(r)@ymin)/cs[2]))) - 1
# Define grd characteristics
grd    <- GridTopology(cellcentre.offset = cc, cellsize = cs, cells.dim = cd)   
#transform to spatial grid dataframe. each cell has a sequential numeric id
sp_grd <- SpatialGridDataFrame(grd,
                               data = data.frame(id = seq(1,(prod(cd)),1)),  # ids are numbers between 1 and ns*nl
                               proj4string = crs(r) )

# Save the "raster fishnet"
out_raster   <- raster(sp_grd) %>%
                setValues(sp_grd@data$id)
temprast     <- tempfile(tmpdir = tempdir(), fileext = ".tif")
writeRaster(out_raster, temprast, overwrite = TRUE)

# "supersample" the raster of the cell numbers

ss_factor = 20  # this indicates how much you increase resolution of the "cells" raster
                # the higher this is, the lower the error in computed percentages

temprast_hr  <- tempfile(tmpdir = tempdir(), fileext = ".tif")
super_raster <- gdalwarp(temprast, temprast_hr, tr = res(r)/ss_factor, output_Raster = TRUE, overwrite = TRUE)

# Now rasterize the input polygons with same extent and resolution of super_raster

tempshapefile <- writeOGR(obj = lots.of.polygons, dsn="tempdir", layer="tempshape", driver="ESRI Shapefile") 
temprastpoly <- tempfile(tmpdir = tempdir(), fileext = ".tif")
rastpoly <- gdal_rasterize(tempshapefile, temprastpoly, tr = raster::res(super_raster),
                           te = extent(super_raster)[c(1,3,2,4)], a = 'id', output_Raster = TRUE)

# Compute Zonal statistics: for each "value" of the  supersampled fishnet raster,
# compute the number of cells which  have a non-zero value  in the supersampled  
# polygons raster (i.e., they belong to one polygon), and divide by the maximum
# possible of cells (equal to ss_factor^2)

cell_nos <- getValues(super_raster)
polyid   <- getValues(rastpoly)
rDT <- data.table(polyid_fc = as.numeric(polyid), cell_nos = as.numeric(cell_nos))
setkey(rDT, cell_nos)

# Use data.table to quickly summarize over cell numbers
count <- rDT[, lapply(.SD, FUN = function(x, na.rm = TRUE) {
                                        100*length(which(x > 0))/(ss_factor^2)
                                          },
                            na.rm = na.rm),
             by = cell_nos]

# Put the results back in the SpatialGridDataFrame and plot
sp_grd@data <- data.frame(count)
sp_grd$polyid_fc[sp_grd$polyid_fc == 0] <- NA
spplot(sp_grd, zcol = 'polyid_fc')

This should be very fast and also scale very well with the number of polygons.

The caveat is that you will have to deal with approximation in the computed percentages ! The error committed depends on how much you "supersample" the raster (here is set to 20 by the ss_factor variable). Higher super-sampling factors lead to lower error, but larger memory requirements and processing times.

I was also thinking that a way to speed-up the "vector based" approaches could be to make an a-priori analysis of the distances between raster cells and the different polygons, which would allow you only to look for intersects between cells and "nearby" polygons. Maybe you could use the bboxes of the polygons to look out for interesting cells....

HTH,

Lorenzo

Margarito

I comment on my own answer : in your particular case you can also use a single multi-polygon, since you are not interested in seeing which cell intersects with which polygon.That would speed-up the approach even more. – Margarito