Why does my Sympy code calculate the first order Taylor series approximation incorrectly?

Question

I have an expression like this

which is entered into Sympy like this (for the sake of a reproducible example in this question)

from sympy import *
expression = Add(Mul(Integer(-1), Float('0.9926375361451395', prec=2), Add(Mul(Float('0.33167082639756074', prec=2), Pow(Symbol('k1'), Float('-0.66666666666666674', prec=2)), Pow(Symbol('n1'), Float('0.66666666666666674', prec=2))), Mul(Float('0.97999999999999998', prec=2), exp(Mul(Integer(-1), Symbol('mu1'))))), Pow(Add(Mul(Float('0.97999999999999998', prec=2), Symbol('k1'), exp(Mul(Integer(-1), Symbol('mu1')))), Mul(Integer(-1), Symbol('k2')), Mul(Pow(Symbol('n1'), Float('0.66666666666666674', prec=2)), Pow(Mul(Symbol('k1'), exp(Mul(Integer(-1), Symbol('mu1')))), Float('0.33333333333333331', prec=2)))), Integer(-1))), Pow(Add(Mul(Float('0.97999999999999998', prec=2), Symbol('k0'), exp(Mul(Integer(-1), Symbol('mu0')))), Mul(Integer(-1), Symbol('k1')), Mul(Pow(Symbol('n0'), Float('0.66666666666666674', prec=2)), Pow(Mul(Symbol('k0'), exp(Mul(Integer(-1), Symbol('mu0')))), Float('0.33333333333333331', prec=2)))), Integer(-1)))

Eyeballing this expression, the first order Taylor approximation for any of the variables, e.g. k1, around some nonzero value should be nonzero, but this code

x = symbol("x")
expression.series(k1, x0 = x, n = 1)

just returns 0. This is a problem because I'm trying to (eventually) calculate a multivariate Taylor series approximation, in a similar vein to this answer, and if one of the series expansions mistakenly evaluates to zero, the whole thing breaks down.

Did I code something wrong, or is my basic calculus just THAT bad and this actually evaluates to zero? From the documentation on series, I'm fairly certain that I'm using it correctly.

Piercing

Answer 1

I think this is a bug related to the way the addition operation handles Orders.

This bug applies only if you are calculating the zero order (n=1) of the Taylor series. To avoid it, you can do

next(expression.series(k1, x0=x, n=None))

which is equivalent to

expression.subs(k1, x0=x)

Here is a simple description of this bug:

from sympy import cos
from sympy.abc import x
cos(x).series(x, x0=1, n=2)

Results in

cos(1) - (x - 1)*sin(1) + O((x - 1)**2, (x, 1))

But

cos(x).series(x, x0=1, n=1)

Results in O(x - 1, (x, 1)), instead of cos(1) + O(x - 1, (x, 1)).

This bug results from a bug in Add

O(x).subs(x,x-1) + 1

Results in O(x - 1, (x, 1)), instead of 1 + O(x - 1, (x, 1)).

Anett

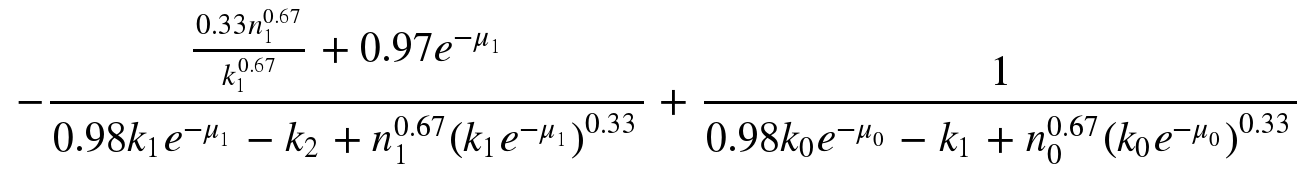
Looks like this bug is fixed in the git master version of SymPy. There, O(x).subs(x,x-1) + 1 gives 1 + O(x - 1, (x, 1)), and the series in question gives O(k₁ - x; k₁ → x). – Chronology