fortran 2d-FFTW inconsistent with C 2d-FFTW results

Question

I am learning how to handle the FFTW package with fortran. To produce an easily verifiable example, I compute the power spectrum of a 2d plane, which I fill with two distinct superpositioned waves. This way, I know exactly where to expect peaks in the power spectrum.

As the FFTW documentation is more extensive for C, I first implemented the algorithm in C, which gives me quite satisfactory results: 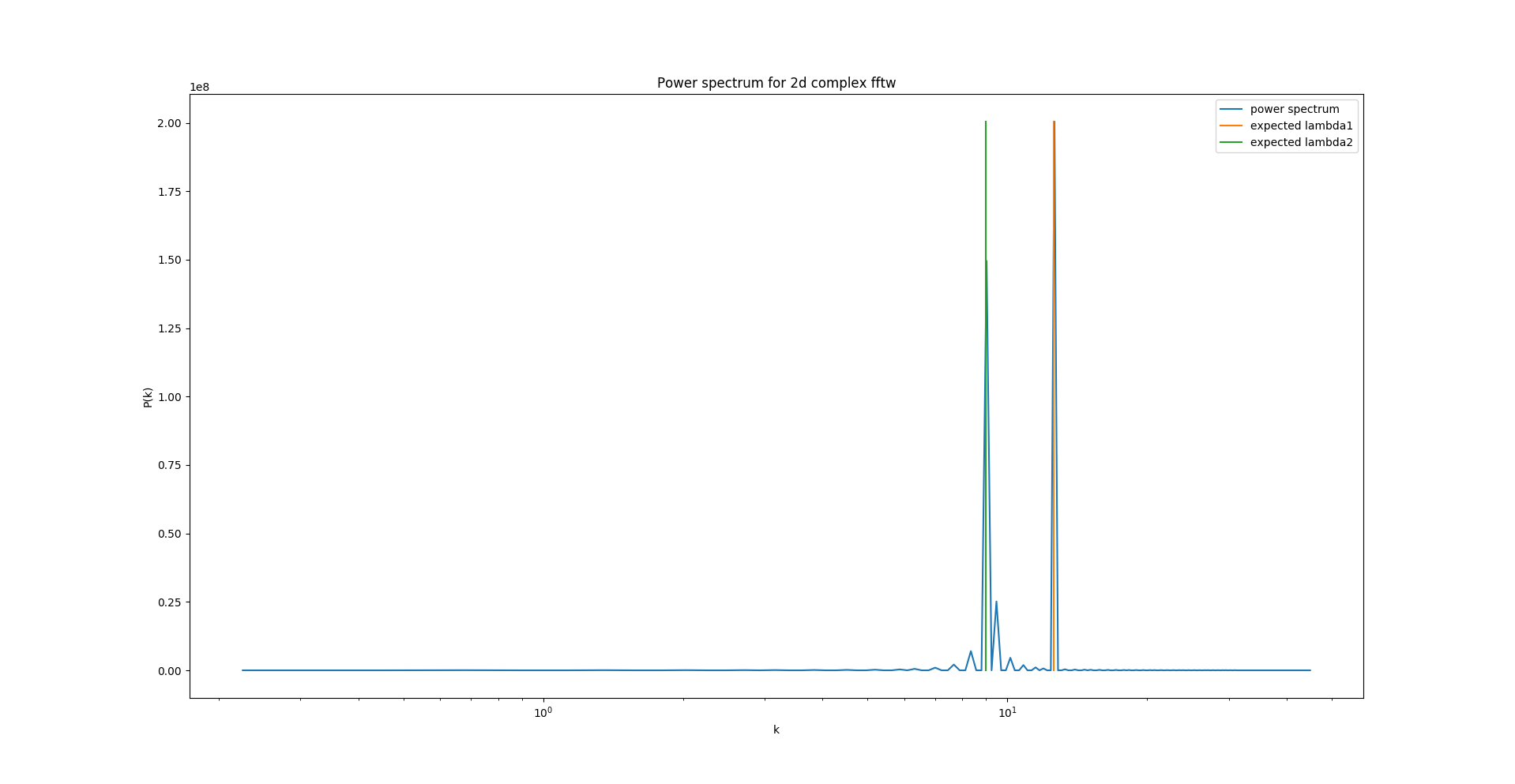"lambda1" and "lambda2" are the known, expected wavelengths. The blue line is the obtained power spectrum.

Then I tried to do exactly the same with fortran, which gives weird results:

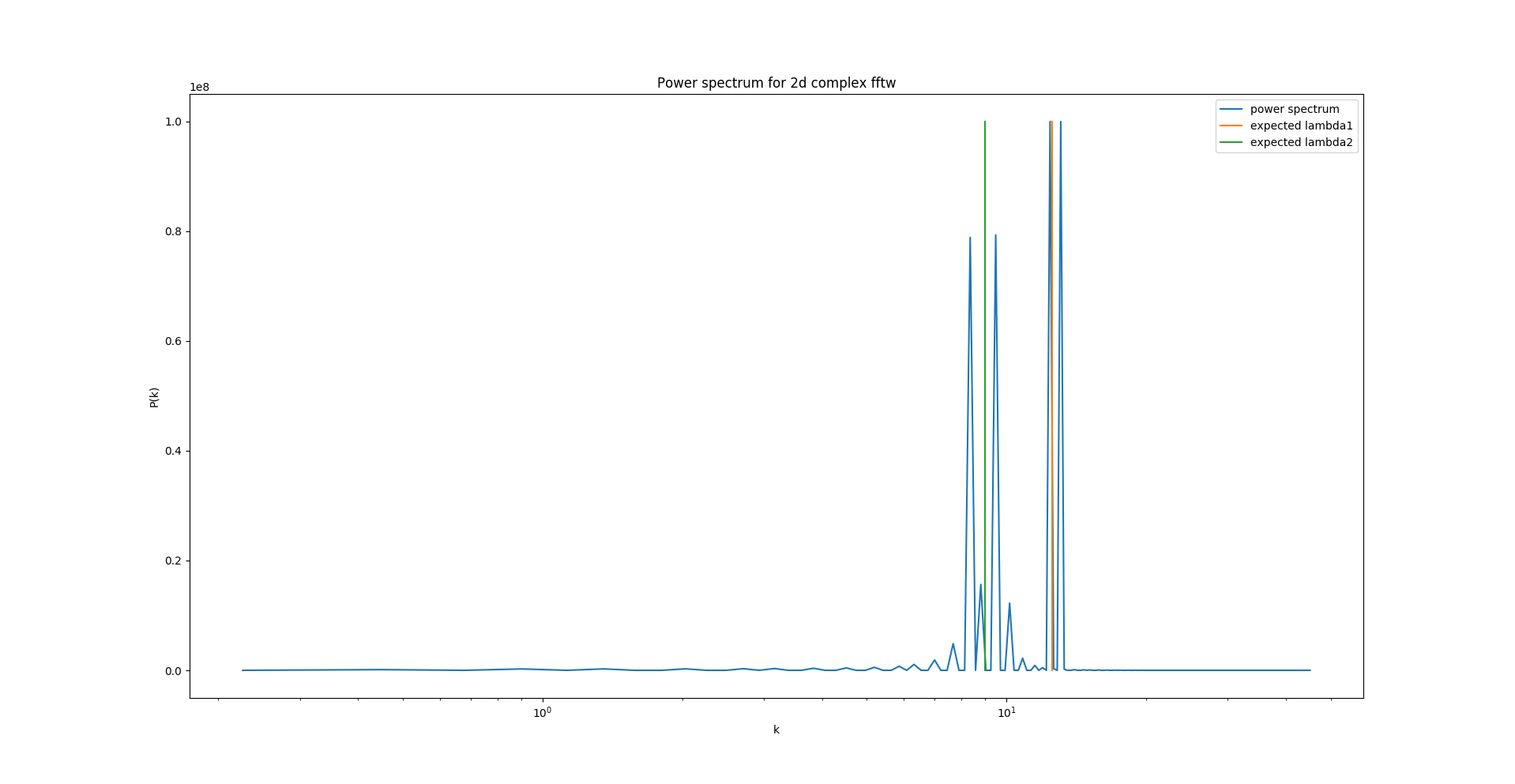
I have no idea where to look for possible errors. The codes execute without a hitch. Can anybody help?

Here is the C code, compiled with: gcc stackexchange.c -o a.out -I/home/myname/.local/include -lfftw3 -lm -g -Wall (gcc 5.4.0)

#include <fftw3.h>
#include <math.h>
#include <stdio.h>
#include <stdlib.h>

int main(void)
{
    // parameters
    int Nx = 200;
    int Ny = 100;            
    int nsamples = 200;
    float pi = 3.1415926;
    float physical_length_x = 20;
    float physical_length_y = 10;
    float lambda1 = 0.5;
    float lambda2 = 0.7;
    float dx = physical_length_x/Nx;
    float dy = physical_length_y/Ny;
    float dkx = 2*pi/physical_length_x;
    float dky = 2*pi/physical_length_y;

    // counters/iterators
    int ind, i, j, ix, iy, ik;

    // power spectra stuff
    float *Pk, *distances_k, d, kmax;
    float *Pk_field;


    // FFTW vars and arrays
    fftw_complex *in, *out;
    fftw_plan my_plan;

    // allocate arrays for input/output
    in  = (fftw_complex *) fftw_malloc(sizeof(fftw_complex) * Nx * Ny);
    out = (fftw_complex *) fftw_malloc(sizeof(fftw_complex) * Nx * Ny);

    // Create Plan
    int n[2]; n[0] = Nx; n[1] = Ny;
    my_plan = fftw_plan_dft(2, n, in, out, FFTW_FORWARD, FFTW_ESTIMATE);

    // fill up array with a wave
    for (i=0; i<Nx; i++){
      for (j=0; j<Ny; j++){
        ind = i*Ny + j;
        in[ind][0] = cos(2.0*pi/lambda1*i*dx) + sin(2.0*pi/lambda2*j*dy);
      }
    }

    // execute fft
    fftw_execute(my_plan); /* repeat as needed */

    // Calculate power spectrum: P(kx, ky) = |F[delta(x,y)]|^2
    Pk_field = malloc(sizeof(float)*Nx*Ny);
    for (i=0; i<Nx; i++){
      for (j=0; j<Ny; j++){
        ind = i*Ny+j;
        Pk_field[ind] = out[ind][0]*out[ind][0] + out[ind][1]*out[ind][1];
      }
    }

    Pk = calloc(nsamples, sizeof(float));
    distances_k = malloc(nsamples*sizeof(float));
    kmax = sqrt(pow((Nx/2+1)*dkx, 2) + pow((Ny/2+1)*dky, 2));
    for(i=0; i<nsamples; i++){
      distances_k[i]= 1.0001*i/nsamples*kmax; // add a little more to make sure kmax will fit
    }

    // histogrammize P(|k|)
    for (i=0; i<Nx; i++){

      if (i<Nx/2+1)
        { ix = i; }
      else
        { ix = -Nx+i; }

      for (j=0; j<Ny; j++){

        if (j<Ny/2+1)
          { iy = j; }
        else
          { iy = -Ny+j; }

        ind = i*Ny + j;
        d = sqrt(pow(ix*dkx,2)+pow(iy*dky,2));

        for(ik=0; ik<nsamples; ik++){
          if (d<=distances_k[ik] || ik==nsamples){
            break;
          }
        }

        Pk[ik] += Pk_field[ind];
      }
    }


    //-----------------------------------
    // write arrays to file.
    // can plot them with plot_fftw.py
    //-----------------------------------
    FILE *filep;
    filep = fopen("./fftw_output_2d_complex.txt", "w");
    for (i=0; i<nsamples; i++){
      fprintf(filep, "%f\t%f\n", distances_k[i], Pk[i]);
    }
    fclose(filep);

    printf("Finished! Written results to ./fftw_output_2d_complex.txt\n");


    //----------------------
    // deallocate arrays
    //----------------------
    fftw_destroy_plan(my_plan);
    fftw_free(in); fftw_free(out);

    return 0;
}

This is the Fortran code, compiled with: gfortran stackexchange.f03 -o a.out -L/home/my_name/.local/lib/ -I/home/my_name/.local/include/ -lfftw3 -g -Wall

program use_fftw

  use,intrinsic :: iso_c_binding
  implicit none
  include 'fftw3.f03'

  integer, parameter     :: dp=kind(1.0d0)
  integer, parameter     :: Nx = 200
  integer, parameter     :: Ny = 100
  integer, parameter     :: nsamples = 200
  real(dp), parameter    :: pi = 3.1415926d0
  real(dp), parameter    :: physical_length_x = 20.d0
  real(dp), parameter    :: physical_length_y = 10.d0
  real(dp), parameter    :: lambda1 = 0.5d0
  real(dp), parameter    :: lambda2 = 0.7d0
  real(dp), parameter    :: dx = physical_length_x/real(Nx,dp)
  real(dp), parameter    :: dy = physical_length_y/real(Ny,dp)
  real(dp), parameter    :: dkx = 2.d0 * pi / physical_length_x
  real(dp), parameter    :: dky = 2.d0 * pi / physical_length_y

  integer :: i, j, ix, iy, ik
  real(dp):: kmax, d

  complex(dp), allocatable, dimension(:,:)    :: arr_in, arr_out, Pk_field
  real(dp), allocatable, dimension(:)         :: Pk, distances_k
  integer*8                                   :: my_plan
  integer                                     :: n(2) = (/Nx, Ny/)


  allocate(arr_in( 1:Nx,1:Ny))
  allocate(arr_out(1:Nx,1:Ny))

  ! call dfftw_plan_dft_2d(my_plan, Nx, Ny, arr_in, arr_out, FFTW_FORWARD, FFTW_ESTIMATE) ! doesn't help either
  call dfftw_plan_dft(my_plan, 2, n, arr_in, arr_out, FFTW_FORWARD, FFTW_ESTIMATE)

  ! fill up wave
  do i = 1, Nx
    do j = 1, Ny
      arr_in(i,j) =cmplx(cos(2.0*pi/lambda1*i*dx)+sin(2.0*pi/lambda2*j*dy) , 0.d0, kind=dp)
    enddo
  enddo

  ! execute fft
  call dfftw_execute_dft(my_plan, arr_in, arr_out)


  allocate(Pk_field(1:Nx, 1:Ny))
  allocate(distances_k(1:nsamples))
  allocate(Pk(1:nsamples))
  Pk=0
  distances_k=0

  ! Get bin distances
  kmax = sqrt(((Nx/2+1)*dkx)**2+((Ny/2+1)*dky)**2)*1.001
  do i = 1, nsamples
    distances_k(i) = i*kmax/nsamples
  enddo

  ! Compute P(k) field, distances field
  do i = 1, Nx
    do j = 1, Ny
      Pk_field(i,j) = arr_out(i,j)*conjg(arr_out(i,j))

      if (i<=Nx/2+1) then
        ix = i
      else
        ix = -Nx+i
      endif
      if (j<=Ny/2+1) then
        iy = j
      else
        iy = -Ny+j
      endif

      d = sqrt((ix*dkx)**2+(iy*dky)**2)

      do ik=1, nsamples
        if (d<=distances_k(ik) .or. ik==nsamples) exit
      enddo

      Pk(ik) = Pk(ik)+real(Pk_field(i,j))
    enddo
  enddo

  ! write file
  open(unit=666,file='./fftw_output_2d_complex.txt', form='formatted')
  do i = 1, nsamples
    write(666, '(2E14.5,x)') distances_k(i), Pk(i)
  enddo
  close(666)


  deallocate(arr_in, arr_out, Pk, Pk_field, distances_k)
  call dfftw_destroy_plan(my_plan)

  write(*,*) "Finished! Written results to fftw_output_2d_complex.txt"

end program use_fftw

For your convenience, this is my short python script that I use to plot the results:

#!/usr/bin/python3

#====================================
# Plots the results of the FFTW
# example programs.
#====================================

import numpy as np
import matplotlib.pyplot as plt
from sys import argv
from time import sleep


errormessage="""
I require an argument: Which output file to plot.
Usage: ./plot_fftw.py <case>
options for case:
    1   fftw_1d_complex.txt
    2   fftw_2d_complex.txt
    3   fftw_1d_real.txt
    4   fftw_2d_real.txt

Please select a case: """



#----------------------
# Hardcoded stuff
#----------------------

file_dict={}
file_dict['1'] = ('fftw_output_1d_complex.txt', '1d complex fftw')
file_dict['2'] = ('fftw_output_2d_complex.txt', '2d complex fftw')
file_dict['3'] = ('fftw_output_1d_real.txt', '1d real fftw')
file_dict['4'] = ('fftw_output_2d_real.txt', '2d real fftw')

lambda1=0.5
lambda2=0.7




#------------------------
# Get case from cmdline
#------------------------

case = ''

def enforce_integer():
    global case
    while True:
        case = input(errormessage)
        try:
            int(case)
            break
        except ValueError:
            print("\n\n!!! Error: Case must be an integer !!!\n\n")
            sleep(2)


if len(argv) != 2:
    enforce_integer()
else:
    try:
        int(argv[1])
        case = argv[1]
    except ValueError:
        enforce_integer()


filename,title=file_dict[case]




#-------------------------------
# Read and plot data
#-------------------------------

k, Pk = np.loadtxt(filename, dtype=float, unpack=True)

fig = plt.figure()

ax = fig.add_subplot(111)
ax.set_title("Power spectrum for "+title)
ax.set_xlabel("k")
ax.set_ylabel("P(k)")
#  ax.plot(k, Pk, label='power spectrum')
ax.semilogx(k[k>0], Pk[k>0], label='power spectrum') # ignore negative k
ax.plot([2*np.pi/lambda1]*2, [Pk.min()-1, Pk.max()+1], label='expected lambda1')
ax.plot([2*np.pi/lambda2]*2, [Pk.min()-1, Pk.max()+1], label='expected lambda2')
ax.legend()

plt.show()

Larder

@francescalus I just did, but there were no changes in the power spectrum. That is to be expected, as the spectrum shouldn't depend on the phase of the wave. – Larder

Indeed. My first guess was "discretization error", but happy to see it isn't that simple. – Autrey

I first suspected a precision error, but weirdly enough, C has a lower precision than Fortran doubles, yet gives the better results.... – Larder

How about the same 0, 1 offset thing when computing/comparing distances_k (still guessing)? – Autrey

The usage of floats instead of doubles in C is strange. fftw_complex is double precision. – Olivenite

Answer 1

In the computation of the histogram, the first index of the loop corresponds to the average, i. e. "zero frequency".

In C, when i=0, j=0, ix=0, iy=0 and d=0. That is correct. For the same item of the array in fortran, the index i=1, then ix=1 and d is not null anymore.

That's for the null frequency, but the whole histogram is sligthly polluted due to the difference of indexing between C and Fortran. In particular, the modification might affect positive frequencies and negative frequencies in different ways, thus triggering the observed double peaks in the plots.

Could you try to modify the computation of ix and iy in Fortran as:

  if (i-1<Nx/2+1) then
    ix = i-1
  else
    ix = -Nx+i-1
  endif
  if (j-1<Ny/2+1) then
    iy = j-1
  else
    iy = -Ny+j-1
  endif

Disconsider

that's it! Although the results are still not exactly the same: here is the updated fortran image: imgur.com/jRtRxJH The first peak (green line) is a bit shifted to the left, ~10% off, while the C version seems way better. Although the general shape of the power spectrum seems very similar. – Larder

The bins are to be corrected as well. distances_k[0] is 0, while distances_k(1) first item of the Fortran array, Could you try distances_k(i) = (i-1)*kmax/nsamples ? – Disconsider

unfortunately, no. Independently of how I define the bins, the loop just bins the values at a higher/lower i – Larder

Short update: I tried comparing the created wave arrays directly to rule out that I'm passing different initial conditions. (This includes your proposed update, changing floats to doubles in the C file and changing i -> i-1 and j->j-1 when generating initial conditions in the fortran file.) I printed the arrays up to 18 decimals, and they are identical. I have no idea what to do now :) – Larder

Investigating the bins of the histograms, it seems that it is distances_k[i]= 1.0001*i/nsamples*kmax; in C, while it is distances_k(i) = i*1.001*kmax/nsamples in Fortran ( the 1.001 is in the previous line). I tried to change for distances_k(i) = (i-1)*1.0001*kmax/nsamples and it seems to help! The artificial frequencies in the cas lambda=0.7 are induced by spectral leakage. Applying a window to attenuate the discontinuity of the periodized frame may improve the power spectrum. – Disconsider