Faster method for creating spatially correlated noise?

Question

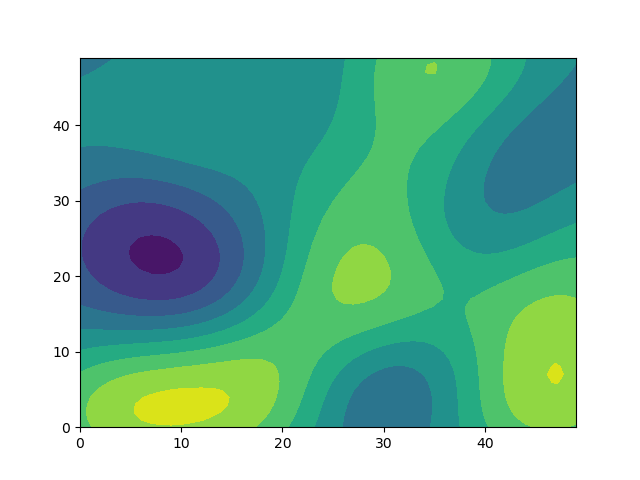
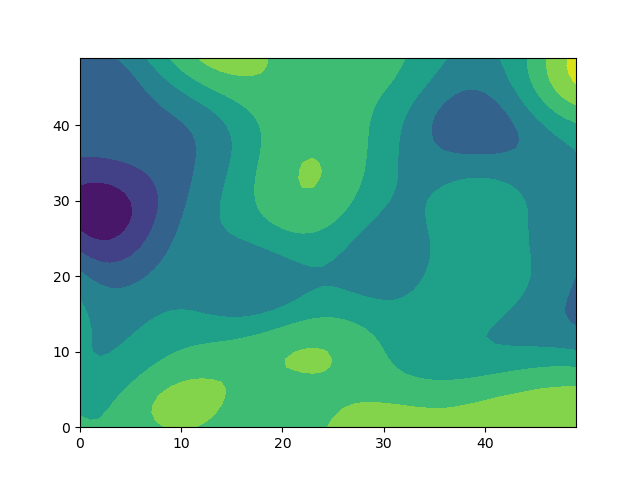
In my current project, I am interested in calculating spatially correlated noise for a large model grid. The noise should be strongly correlated over short distances, and uncorrelated over large distances. My current approach uses multivariate Gaussians with a covariance matrix specifying the correlation between all cells.

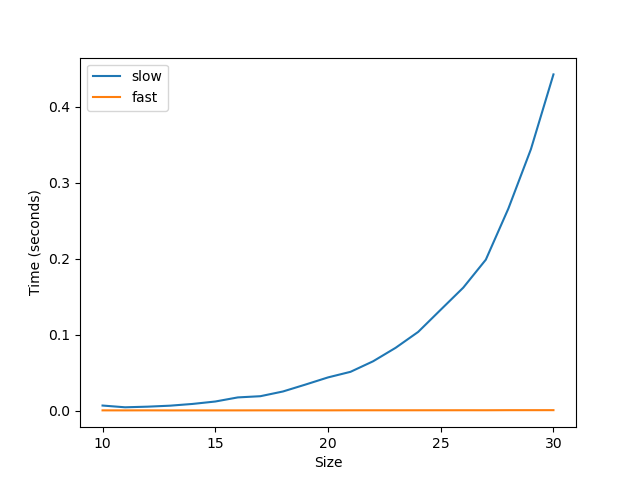
Unfortunately, this approach is extremely slow for large grids. Do you have a recommendation of how one might generate spatially correlated noise more efficiently? (It doesn't have to be Gaussian)

import scipy.stats
import numpy as np
import scipy.spatial.distance
import matplotlib.pyplot as plt

# Create a 50-by-50 grid; My actual grid will be a LOT larger
X,Y = np.meshgrid(np.arange(50),np.arange(50))

# Create a vector of cells
XY = np.column_stack((np.ndarray.flatten(X),np.ndarray.flatten(Y)))

# Calculate a matrix of distances between the cells
dist = scipy.spatial.distance.pdist(XY)
dist = scipy.spatial.distance.squareform(dist)

# Convert the distance matrix into a covariance matrix
correlation_scale = 50
cov = np.exp(-dist**2/(2*correlation_scale)) # This will do as a covariance matrix

# Sample some noise !slow!
noise = scipy.stats.multivariate_normal.rvs(
        mean = np.zeros(50**2),
        cov = cov)

# Plot the result
plt.contourf(X,Y,noise.reshape((50,50)))

Aloe

Answer 1

Faster approach:

• Generate spatially uncorrelated noise.
• Blur with Gaussian filter kernel to make noise spatially correlated.

Since the filter kernel is rather large, it is a good idea to use a convolution method based on Fast Fourier Transform.

import numpy as np
import scipy.signal
import matplotlib.pyplot as plt

# Compute filter kernel with radius correlation_scale (can probably be a bit smaller)
correlation_scale = 50
x = np.arange(-correlation_scale, correlation_scale)
y = np.arange(-correlation_scale, correlation_scale)
X, Y = np.meshgrid(x, y)
dist = np.sqrt(X*X + Y*Y)
filter_kernel = np.exp(-dist**2/(2*correlation_scale))

# Generate n-by-n grid of spatially correlated noise
n = 50
noise = np.random.randn(n, n)
noise = scipy.signal.fftconvolve(noise, filter_kernel, mode='same')
plt.contourf(np.arange(n), np.arange(n), noise)
plt.savefig("fast.png")

Sample output of this method:

Sample output of slow method from question:

Image size vs running time:

Davis