What does "subsets" mean in UML exactly?

Question

The UML 2.5.1 specification does not define the keyword subsets very well. I found the following in section 6.4.2:

The constraint {subsets endA} means that the association end to which this constraint is applied subsets the association end endA.

Consider the following diagram:

Intuitively, I would think this means the following:

1. A Person can be a member of zero or more Clubs.
2. A Person can be the leader of at most one Club.
3. If a Person is the leader of a Club, then he/she is also a member of the same Club.
4. If a Person is the leader of a Club, then he/she can still be a member of other Clubs at the same time.

I wonder if statement 4 is correct. In a discussion with Jim L. in the comments under his answer to another question, Jim wrote

You can’t restrict the cardinality of a subset and still have an element of the superset that violates the restriction.

If I understand this well, if a Person is the leader of a Club, then he/she cannot be a member of another Club.

Is there some place in the UML specs that defines subsets better than what I found?

Prospector

I had 292 matches for subsets in the specs... – Sundew

...and that were all but one just usages of it. The only definition is that you found. So it's probably left to speculation and the OMG guys should be questioned here. However, I think that Jim is right and this is more a logical puzzle. – Sundew

My guess would be that the leader is one of the members and the above is perfectly fine. – Sundew

I agree with everything except "if a Person is the leader of a Club, then he/she cannot be a member of another Club." – Stratus

I think that @JimL. 's comment confirms your understanding and the only thing he'd disagree is the opposite of 4. – Irradiation

@Christophe: I agree with your last comment. – Stratus

Answer 1

The definition

You may find what you're looking for in the section 9.5 about properties:

Properties are StructuralFeatures that represent the attributes of Classifiers, the memberEnds of Associations, and the parts of StructuredClassifiers.

The UML specs underline that it applies as well to associations ends (section 11.5.3.1, p.200):

Subsetting of Association ends has the meaning specified for Property (see 9.5.3).

More precisely, the semantics of subsetting are defined in section 9.5.3 (page 112):

A Property may be marked as the subset of another subsettedProperty. In this case, calculate a set by eliminating duplicates from the collection of values denoted by the subsetting property in some context. Then that set shall be included in (or the same as) a set calculated by eliminating duplicates from the collection of values denoted by the subsettedProperty in the same context.

Remark: There is no definition of subsetting an association as a whole (i.e. beyond the association end, like in your example). But a paragraph on specialization reasons on sets of links (i.e the tuples of classified values at each end of the association) instead of sets of values. The existing definition could easily be applied likewise.

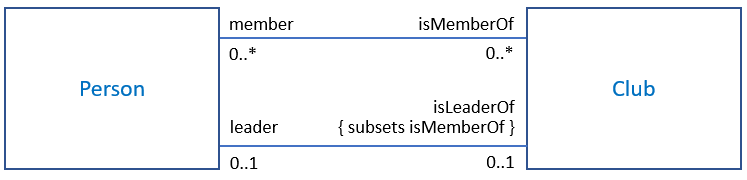
Application to your example

Statement 4 appears correct. Take a person A that is member of the club C1, C2, C3, C4, and at the same time leader of C1:

The definition requires that the set of unique values in the subsetting property isLeaderOf, i.e.{ C1 } shall be included in the set of unique values of the subsetted property isMemberOf, i.e. { C1, C2, C3, C4 }. The upper bound of the multiplicity of isLeaderOf does not allow to be leader of more than one club. So it'll stay C1 only. The inclusion requirement implies that if A is leader of C1, C1 must be among the values of club memberships. You could add as many more club memberships, as you want, as long as C1 remains in. Even adding multiple C1 memberships would not change the truth of your statement.

In your example, the upper bound 1 simplifies the reasoning. In the more general case, values of the sets are not necessarily unique. So some care is required when making claims about lower and upper bound of multiplicities, since duplicate values could create tricky situations. However, the inclusion requirement is purposely defined based on unique values.

Statement 3 is more tricky and requires deduction: You didn't subset the opposite association end. This means that a club C could have members M1, M2, M3, and could have a leader L, but nothing guarantees that the leader is member of the same club; You could even have a leader without any member:

• Subsetting leader as well would easily solve the issue.
• But even as it is, leader and members being persons, and thanks to the upper bound of 1, we can deduce that such a situation would not be possible, and consequently that statement 3 is true as well.

Irradiation

Looks like that's about properties and not about associatons. – Sundew

@qwerty_so: "Properties are StructuralFeatures that represent the attributes of Classifiers, the memberEnds of Associations, and the parts of StructuredClassifiers." As far as I know, the subsetting applies to the member end. By the way, I'm pretty sure that this definition could also allow us in this specific case to demonstrate that leader subsets member. – Irradiation

I always found the separartion of association (ends) and properties most confusing (and it still leads to much confusion). That late dot-notation is some kind of straw the OMG created to save then from drowning in their own swamp. There might be some esoteric background though that did not make it into my grey matter. – Sundew

@qwerty_so: what separation of association ends and properties? The difference is the value of the meta-property called association. See Figure 9.10 in the UML 2.5 spec (which is all I have handy at the moment). Section 9.5.3 says, "When related to an Association via memberEnd [the inverse of association] it represents an end of the Association." – Stratus

Great reference into the UML spec, thanks!! About statement 3. You wrote "thanks to the upper bound of 1". But suppose the multiplicity of isLeaderOf is 0..* instead of 0..1, then statement 3 would still be true, wouldn't it? – Prospector

@Prospector thank you! Indeed, the 0..1 allowed a very quick logical deduction, without having to think about duplicates. In the slightly different scenario, with 0..* isLeaderOf, I come still to the same conclusion, but with an ambiguity: you could have someone who is leader several times of the same club (it sounds absurd but it would be compliant; in case of doubt, think of a case with an association class to make it more tangible). You would then be sure that the person is member of the same club, but you have no guarantee that it has the same number of memberships. – Irradiation

@Christophe: mentioning "duplicates", you bring up a good point about an oddity in UML: the isUnique meta-property of a Property. I willfully ignore the unwanted possibility of association ends having duplicates and making an association different from a relation. Perhaps this will burn me some day. – Stratus

@JimL. @Christophe, isUnique is true by default (section 7.8.8.5 of the UML 2.5.1 spec). Duplicates only occur if { unique } is explicitly specified. The case with an association class is different (see section 11.5.3.2 of the UML 2.5.1 spec: "Even when all ends of the AssociationClass have isUnique=true, it is possible to have several instances associating the same set of instances of the end Classes"). – Prospector

@Christophe: looking at only the association ends of an association class, you can get what look like duplicate values on the ends because one or more other attributes widen the “tuple“. For example, you can add an id attribute to the end properties left and right to form ⟨ id, left, right ⟩. – Stratus

@Prospector this is excellent news. My practice is like @JimL. : I willfully forget the { unique }, but with bad conscience. Knowing that isUnique is true by default makes me feel very good, actually. And my fear from undesired duplicates comes indeed from the association classes. So the issue with the potential duplicates is a non-issue. By the way I think you meant " Duplicates only occur if { nonunique } is explicitly specified, insnt' it ? – Irradiation

@Irradiation Ah, yes, nonunique of course. – Prospector

Answer 2

In relation to your question,

In the context of UML that is the official definition that you cited.

With your statement. Your statement 4 is correct but as mentioned by Jim the cardinality shouldn't be restricted.

You can have 1 or more leaders of a club along with 1 or more leaders for an individual club.

In addition, subsets help define inheritance. For example, in your diagram if Person is a subset of Club, and they are a leader of the club then automatically they are a member.

It can get a bit nit-picky with logic as in the diagram, the subset does not only inherit from the parent class (Club) but also has its own properties (Person) and at the same time points back to the parent.

Hopefully the links below, outline what I am trying to say.

Some useful links for context:

• What subset constraint means in the UML class diagram

• https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.138.5537&rep=rep1&type=pdf

• https://newbedev.com/how-to-use-subsetted-property-in-uml

Afterdinner

"You can have 1 or more leaders of a club"? I disagree. – Stratus

What do you mean by "the cardinality shouldn't be restricted"? Is the diagram invalid? – Prospector