Multiple types for f in this picture?

Question

https://youtu.be/brE_dyedGm0?t=1362

data T a where
  T1 :: Bool -> T Bool
  T2 :: T a

f x y = case x of
  T1 x -> True
  T2   -> y

Simon is saying that f could be typed as T a -> a -> a, but I would think the return value MUST be a Bool since that is an explicit result in a branch of the case expression. This is in regards to Haskell GADTs. Why is this the case?

Pless

Answer 1

This is kind of the whole point of GADTs. Matching on a constructor can cause additional type information to come into scope.

Let's look at what happens when GHC checks the following definition:

f :: T a -> a -> a
f x y = case x of
    T1 _ -> True
    T2   -> y

Let's look at the T2 case first, just to get it out of the way. y and the result have the same type, and T2 is polymorphic, so you can declare its type is also T a. All good.

Then comes the trickier case. Note that I removed the binding of the name x inside the case as the shadowing might be confusing, the inner value isn't used, and it doesn't change anything in the explanation. When you match on a GADT constructor like T1, one that explicitly sets a type variable, it introduces additional constraints inside that branch which add that type information. In this case, matching on T1 introduces a (a ~ Bool) constraint. This type equality says that a and Bool match each other. Therefore the literal True with type Bool matches the a written in the type signature. y isn't used, so the branch is consistent with T a -> a -> a.

So it all matches up. T a -> a -> a is a valid type for that definition. But as Simon is saying, it's ambiguous. T a -> Bool -> Bool is also a valid type for that definition. Neither one is more general than the other, so the definition doesn't have a principle type. So the definition is rejected unless a type is provided, because inference cannot pick a single most-correct type for it.

Dambro

so how I annotate the function comes down to how I want it to be used? like if i go with T a -> Bool -> Bool then the compiler won't allow f T2 1 and that's basically the difference? – Pless

@Pless Yes. When you're using a GADT, you tend to have something in mind that means you know which case you want. It's only in these very silly example cases that it's hard for you to pick a type, as the code's author. – Dambro

Answer 2

A value of type T a with a different from Bool can never have the form T1 x (since that has only type T Bool).

Hence, in such case, the T1 x branch in the case becomes inaccessible and can be ignored during type checking/inference.

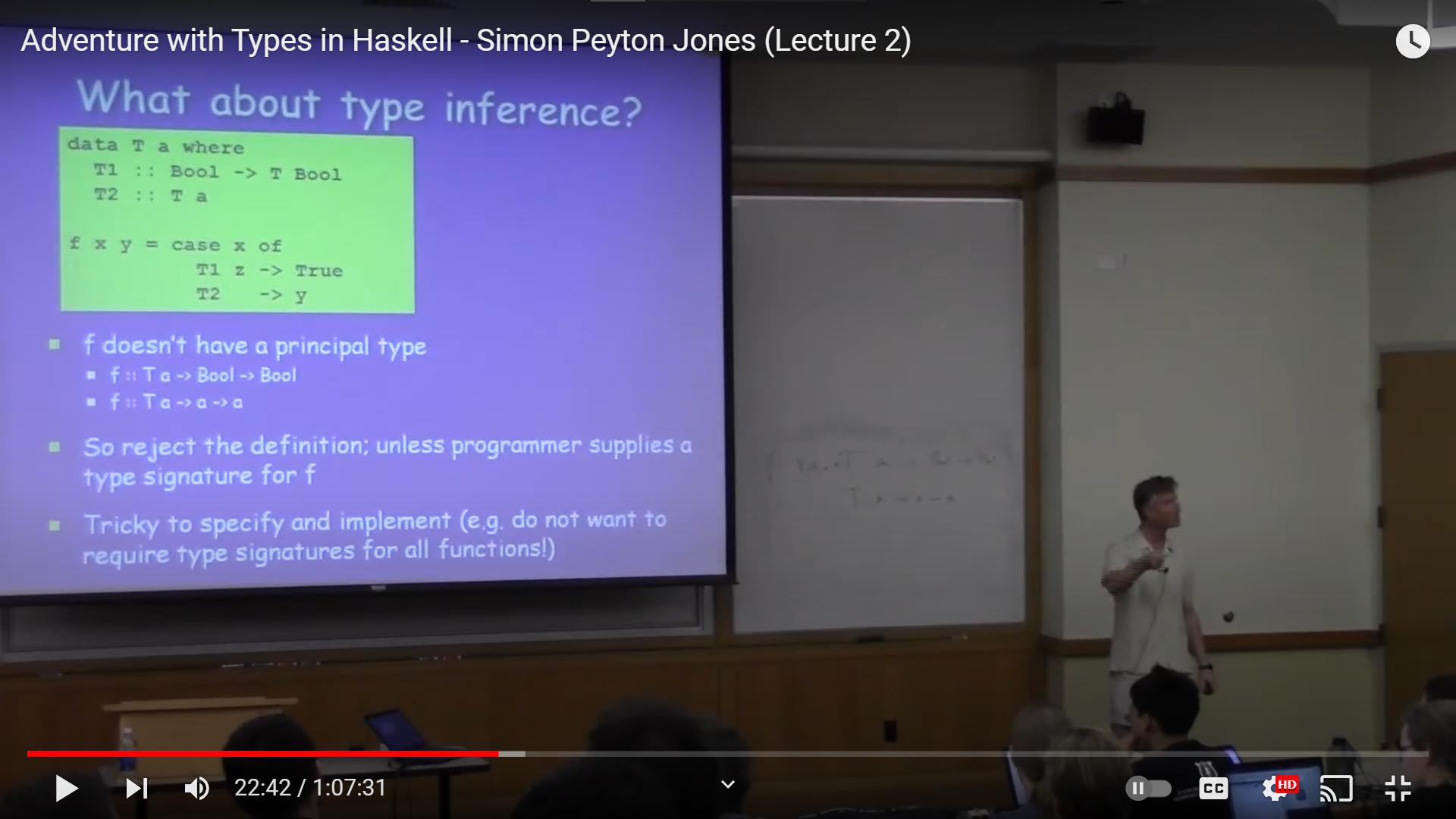
More concretely: GADTs allow the type checker to assume type-level equations during pattern matching, and exploit such equations later on. When checking

f :: T a -> a -> a
f x y = case x of
  T1 x -> True
  T2   -> y

the type checker performs the following reasoning:

f :: T a -> a -> a
f x y = case x of
  T1 x -> -- assume: a ~ Bool
          True  -- has type Bool, hence it has also type a
  T2   -> -- assume: a~a  (pointless)
          y     -- has type a

Thanks to GADTs, both branches of the case have type a, hence the whole case expression has type a and the function definition type checks.

More generally, when x :: T A and the GADT constructor was defined as K :: ... -> T B then, when type checking we can make the following assumption:

case x of
  K ... ->  -- assume: A ~ B

Note that A and B can be types involving type variables (as in a~Bool above), so that allows one obtain useful information about them and exploit it later on.

Rachelrachele