How exactly does tail recursion work?

Question

I almost understand how tail recursion works and the difference between it and a normal recursion. I only don't understand why it doesn't require stack to remember its return address.

// tail recursion
int fac_times (int n, int acc) {
    if (n == 0) return acc;
    else return fac_times(n - 1, acc * n);
}

int factorial (int n) {
    return fac_times (n, 1);
}

// normal recursion
int factorial (int n) {
    if (n == 0) return 1;
    else return n * factorial(n - 1);
}

There is nothing to do after calling a function itself in a tail recursion function but it doesn't make sense for me.

Cheops

Tail recursion is "normal" recursion. It only means that the recursion occurs at the end of the function. – Failure

... But it can be implemented in a different way at the IL level than normal recursion, reducing stack depth. – Lazuli

BTW, gcc can perform tail recursion elimination on the "normal" example here. – Coad

In reference to my above comment, see https://mcmap.net/q/176075/-how-to-recognize-what-is-and-what-is-not-tail-recursion . – Coad

@Lazuli What is "IL level"? – Adrianadriana

Read Lambda: the Ultimage GOTO, one of the original Scheme papers. – Whitmer

@Adrianadriana - I'm a C# dev, so my "assembly language" is MSIL or just IL. For C/C++, replace IL with ASM. – Lazuli

@dmckee I see nothing in that reference that says gcc is performing the sort of rewrite of non-tail recursive code into tail recursive code. – Ultramicrometer

I think we should be clear about the terms: what the OP is asking about is tail recursion optimization. Tail recursion may or may not be optimized, and it is the optimization that eliminates a need for an extra stack frame. – Incline

@ShannonSeverance I found that gcc is doing it by the simple expedient examining the emitted assembly code with without -O3. The link is for an earlier discussion that covers very similar ground and discusses what is necessary to implement this optimization. – Coad

Answer 1

The compiler is simply able to transform this

int fac_times (int n, int acc) {
    if (n == 0) return acc;
    else return fac_times(n - 1, acc * n);
}

into something like this:

int fac_times (int n, int acc) {
label:
    if (n == 0) return acc;
    acc *= n--;
    goto label;
}

Mossback

@AlexeyFrunze if else return fac_times(n - 1, acc * n); was like else return fac_times(n, acc * n); so recursion goes in infinite loop in that case too compiler will do what you have said in ur answer? – Careless

@Mr.32 I don't understand your question. I converted the function into an equivalent one but without explicit recursion (that is, without explicit function calls). If you change the logic into something non-equivalent, you may indeed make the function loop forever in some or all cases. – Mossback

So tails recursion is effective only because of compiler optimising it? And otherwise it would be the same as a normal recursion in terms of stack memory wise? – Cheops

Yep. If the compiler cannot reduce recursion to a loop, you are stuck with recursion. All or nothing. – Mossback

@AlanDert: correct. You can also consider tail recursion to be a special case of the "tail call optimization", special because the tail call happens to be to the same function. In general, any tail call (with the same requirements on "no work left to do" as apply to tail recursion, and where the return value of the tail call is directly returned) can be optimized if the compiler can make the call in a way that sets up the return address of the called function to be the return address of the function making the tail call, instead of the address from which the tail call was made. – Myramyrah

@AlexeyFrunze thanks got it...In my case i got function call forever ....tail recursion doesnt optimise code and due to too much functinon call i got segmentation fault..! – Careless

@AlanDert in C this is just an optimization not enforced by any standard, so portable code should not depend on it. But there are languages (Scheme is one example), where tail recursion optimization is enforced by the standard, so you don't need to worry that it will stack overflow in some environments. – Valladares

What if the recursive function was, for example, a sort algorithm that sorted in place and doesn't have an actual return function? Would leaving out the 'return' in the last statement still allow the compiler to perform tail recursion optimization? Or should you add 'return' to the final statement even if it isn't actually returning anything? – Pax

Answer 2

You ask why "it doesn't require stack to remember its return address".

I would like to turn this around. It does use the stack to remember the return address. The trick is that the function in which the tail recursion occurs has its own return address on the stack, and when it jumps to the called function, it will treat this as it's own return address.

Concretely, without tail call optimization:

f: ...
   CALL g
   RET
g:
   ...
   RET

In this case, when g is called, the stack will look like:

   SP ->  Return address of "g"
          Return address of "f"

On the other hand, with tail call optimization:

f: ...
   JUMP g
g:
   ...
   RET

In this case, when g is called, the stack will look like:

   SP ->  Return address of "f"

Clearly, when g returns, it will return to the location where f was called from.

EDIT: The example above use the case where one function calls another function. The mechanism is identical when the function calls itself.

Otoole

This is a much better answer than the other answers. The compiler most likely doesn't have some magical special case for converting tail recursive code. It just performs a normal last call optimization that happens to go to the same function. – Colangelo

Answer 3

Tail recursion can usually be transformed into a loop by the compiler, especially when accumulators are used.

// tail recursion
int fac_times (int n, int acc = 1) {
    if (n == 0) return acc;
    else return fac_times(n - 1, acc * n);
}

would compile to something like

// accumulator
int fac_times (int n) {
    int acc = 1;
    while (n > 0) {
        acc *= n;
        n -= 1;
    }
    return acc;
}

Marker

Not as clever as Alexey's implementation... and yes that's a compliment. – Sym

Actually, the result looks simpler but I think the code to implement this transformation would be FAR more "clever" than either label/goto or just tail call elimination (see Lindydancer's answer). – Dielu

If this is all tail recursion is, then why do people get so excited about it? I don't see anyone getting excited about while loops. – Nedanedda

@BuhBuh: This doesn't have stackoverflow, and avoids the stack push/popping of parameters. For a tight loop like this it can make a world of difference. Other than that people ought not be excited. – Orpine

Answer 4

There are two elements that must be present in a recursive function:

1. The recursive call
2. A place to keep count of the return values.

A "regular" recursive function keeps (2) in the stack frame.

The return values in regular recursive function are composed of two types of values:

• Other return values
• Result of the owns function computation

Let's look at your example:

int factorial (int n) {
    if (n == 0) return 1;
    else return n * factorial(n - 1);
}

The frame f(5) "stores" the result of it's own computation (5) and the value of f(4), for example. If i call factorial(5), just before the stack calls begin to collapse, i have:

 [Stack_f(5): return 5 * [Stack_f(4): 4 * [Stack_f(3): 3 * ... [1[1]]

Notice that each stack stores, besides the values i mentioned, the whole scope of the function. So, the memory usage for a recursive function f is O(x), where x is the number of recursive calls i have to made. So, if i needb 1kb of RAM to calculate factorial(1) or factorial(2), i need ~100k to calculate factorial(100), and so on.

A Tail Recursive function put (2) in it's arguments.

In a Tail Recursion, i pass the result of the partial calculations in each recursive frame to the next one using parameters. Let's see our factorial example, Tail Recursive:

int factorial (int n) {
    int helper(int num, int accumulated)
        {
            if num == 0 return accumulated
            else return helper(num - 1, accumulated*num)
        }
    return helper(n, 1)    
}

Let's look at it's frames in factorial(4):

[Stack f(4, 5): Stack f(3, 20): [Stack f(2,60): [Stack f(1, 120): 120]]]]

See the differences? In "regular" recursive calls the return functions recursively compose the final value. In Tail Recursion they only reference the base case (last one evaluated). We call accumulator the argument that keeps track of the older values.

Recursion Templates

The regular recursive function go as follows:

type regular(n)
    base_case
    computation
    return (result of computation) combined with (regular(n towards base case))

To transform it in a Tail recursion we:

• Introduce a helper function that carries the accumulator
• run the helper function inside the main function, with the accumulator set to the base case.

Look:

type tail(n):
    type helper(n, accumulator):
        if n == base case
            return accumulator
        computation
        accumulator = computation combined with accumulator
        return helper(n towards base case, accumulator)
    helper(n, base case)

See the difference?

Tail Call optimization

Since no state is being stored on the Non-Border-Cases of the Tail Call stacks, they aren't so important. Some languages/interpreters then substitute the old stack with the new one. So, with no stack frames constraining the number of calls, the Tail Calls behave just like a for-loop in these cases.

It's up to your compiler to optimize it, or no.

Forecast

Answer 5

Here is a simple example that shows how recursive functions work:

long f (long n)
{

    if (n == 0) // have we reached the bottom of the ocean ?
        return 0;

    // code executed in the descendence

    return f(n-1) + 1; // recurrence

    // code executed in the ascendence

}

Tail recursion is a simple recursive function, where recurrence is done at the end of the function, thus no code is done in ascendence, which helps most compilers of high-level programming languages to do what is known as Tail Recursion Optimization, also has a more complex optimization known as the Tail recursion modulo

Genius

Answer 6

The recursive function is a function which calls by itself

It allows programmers to write efficient programs using a minimal amount of code.

The downside is that they can cause infinite loops and other unexpected results if not written properly.

I will explain both Simple Recursive function and Tail Recursive function

In order to write a Simple recursive function

1. The first point to consider is when should you decide on coming out of the loop which is the if loop
2. The second is what process to do if we are our own function

From the given example:

public static int fact(int n){
  if(n <=1)
     return 1;
  else 
     return n * fact(n-1);
}

From the above example

if(n <=1)
     return 1;

Is the deciding factor when to exit the loop

else 
     return n * fact(n-1);

Is the actual processing to be done

Let me the break the task one by one for easy understanding.

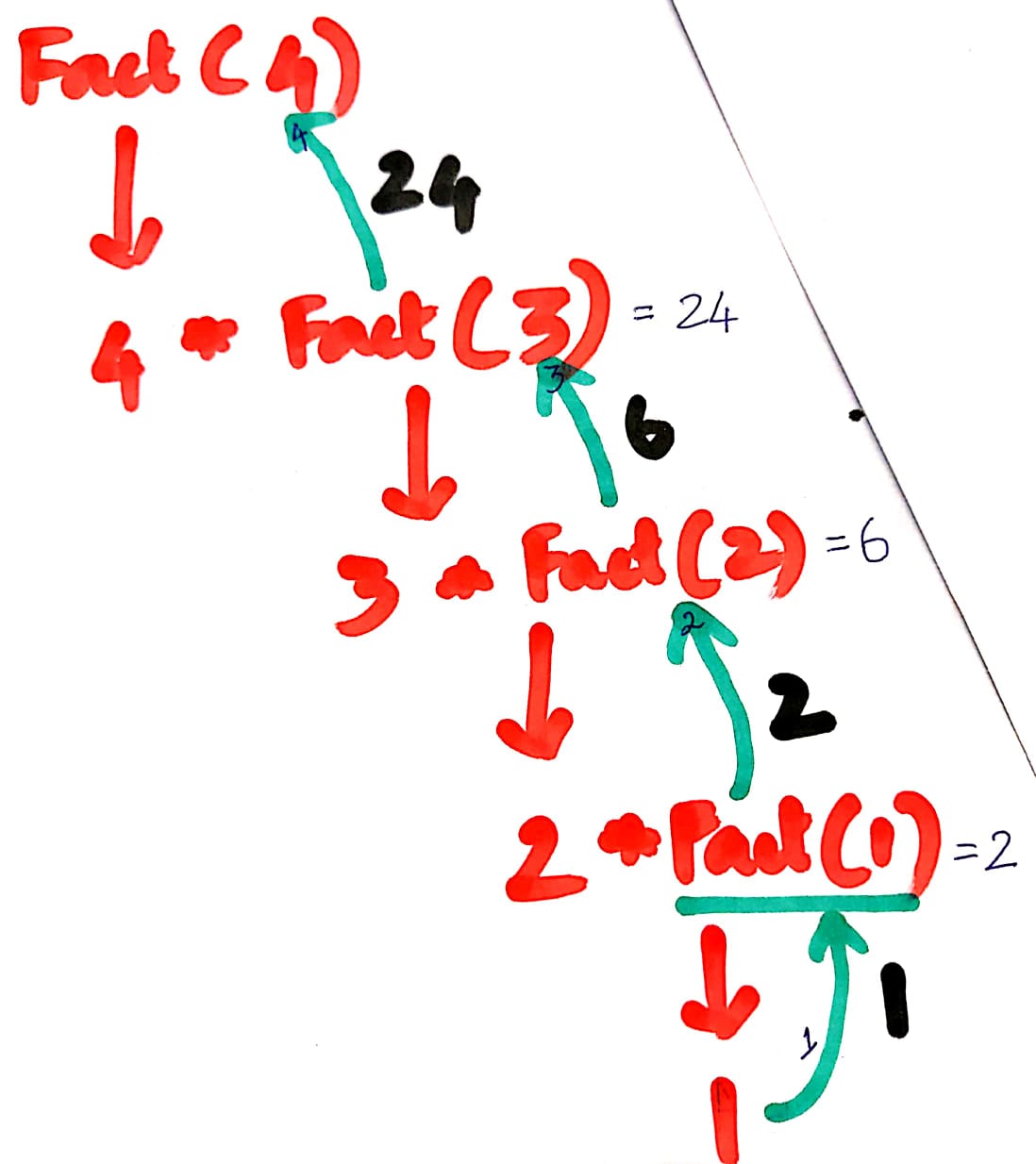
Let us see what happens internally if I run fact(4)

1. Substituting n=4

public static int fact(4){
  if(4 <=1)
     return 1;
  else 
     return 4 * fact(4-1);
}

If loop fails so it goes to else loop so it returns 4 * fact(3)

2. In stack memory, we have 4 * fact(3)

   Substituting n=3

public static int fact(3){
  if(3 <=1)
     return 1;
  else 
     return 3 * fact(3-1);
}

If loop fails so it goes to else loop

so it returns 3 * fact(2)

Remember we called ```4 * fact(3)``

The output for fact(3) = 3 * fact(2)

So far the stack has 4 * fact(3) = 4 * 3 * fact(2)

3. In stack memory, we have 4 * 3 * fact(2)

   Substituting n=2

public static int fact(2){
  if(2 <=1)
     return 1;
  else 
     return 2 * fact(2-1);
}

If loop fails so it goes to else loop

so it returns 2 * fact(1)

Remember we called 4 * 3 * fact(2)

The output for fact(2) = 2 * fact(1)

So far the stack has 4 * 3 * fact(2) = 4 * 3 * 2 * fact(1)

3. In stack memory, we have 4 * 3 * 2 * fact(1)

   Substituting n=1

public static int fact(1){
  if(1 <=1)
     return 1;
  else 
     return 1 * fact(1-1);
}

If loop is true

so it returns 1

Remember we called 4 * 3 * 2 * fact(1)

The output for fact(1) = 1

So far the stack has 4 * 3 * 2 * fact(1) = 4 * 3 * 2 * 1

Finally, the result of fact(4) = 4 * 3 * 2 * 1 = 24

The Tail Recursion would be

public static int fact(x, running_total=1) {
    if (x==1) {
        return running_total;
    } else {
        return fact(x-1, running_total*x);
    }
}

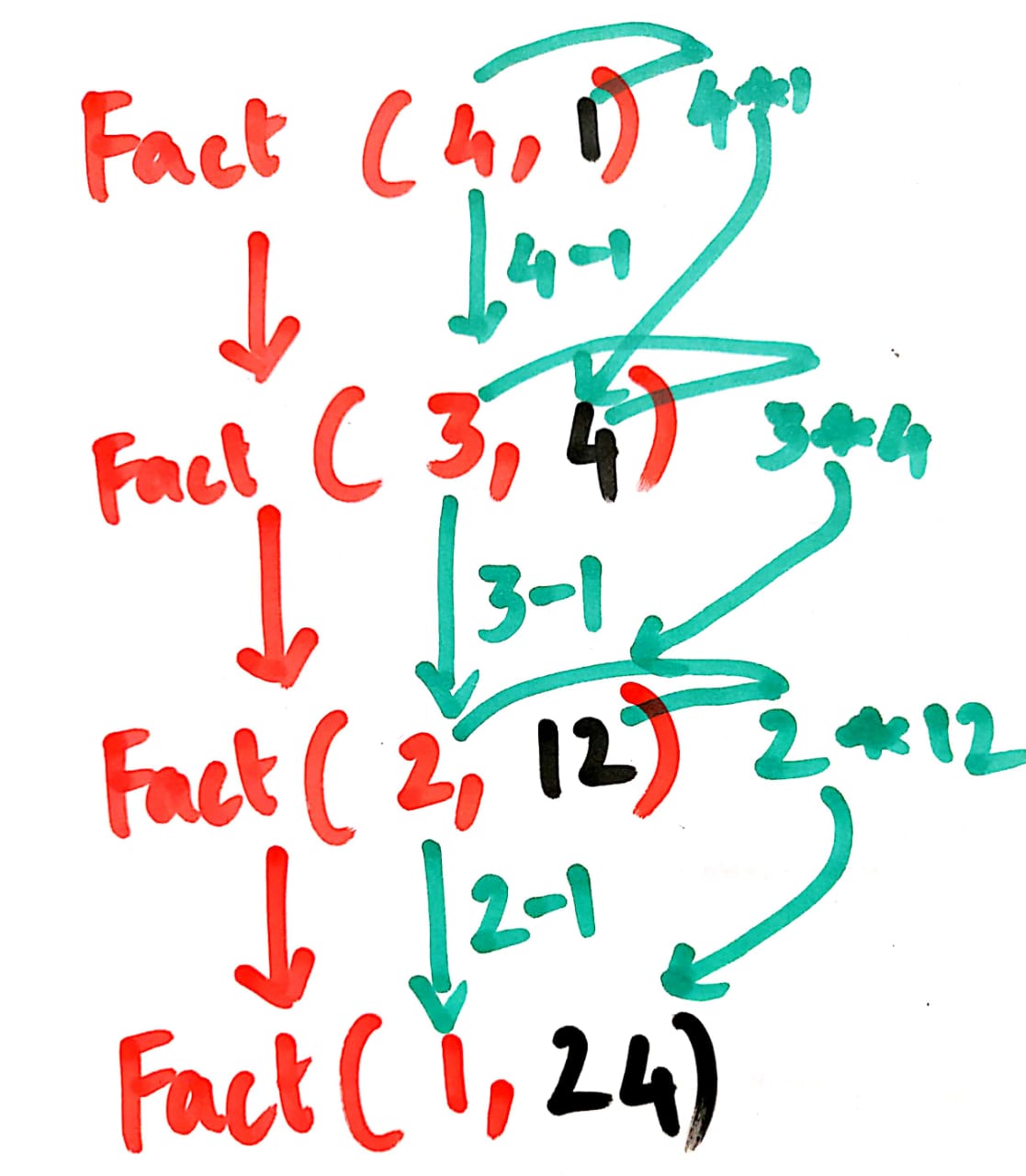
1. Substituting n=4

public static int fact(4, running_total=1) {
    if (x==1) {
        return running_total;
    } else {
        return fact(4-1, running_total*4);
    }
}

If loop fails so it goes to else loop so it returns fact(3, 4)

2. In stack memory, we have fact(3, 4)

   Substituting n=3

public static int fact(3, running_total=4) {
    if (x==1) {
        return running_total;
    } else {
        return fact(3-1, 4*3);
    }
}

If loop fails so it goes to else loop

so it returns fact(2, 12)

2. In stack memory, we have fact(2, 12)

   Substituting n=2

public static int fact(2, running_total=12) {
    if (x==1) {
        return running_total;
    } else {
        return fact(2-1, 12*2);
    }
}

If loop fails so it goes to else loop

so it returns fact(1, 24)

3. In stack memory, we have fact(1, 24)

   Substituting n=1

public static int fact(1, running_total=24) {
    if (x==1) {
        return running_total;
    } else {
        return fact(1-1, 24*1);
    }
}

If loop is true

so it returns running_total

The output for running_total = 24

Finally, the result of fact(4,1) = 24

Knuth

Answer 7

My answer is more of a guess, because recursion is something relating to internal implementation.

In tail recursion, the recursive function is called at the end of the same function. Probably compiler can optimize in below way:

1. Let the ongoing function wind up (i.e. used stack is recalled)
2. Store the variables which are going to be used as arguments to the function in a temporary storage
3. After this, call the function again with the temporarily stored argument

As you can see, we are winding up the original function before the next iteration of the same function, so we are not actually "using" the stack.

But I believe if there are destructors to be called inside the function then this optimization may not apply.

Cesta

Answer 8

Compiler is enough intelligent to understand tail recursion.In case, while returning back from a recursive call,there is no pending operation and recursive call is the last statement, fall under the category of tail recursion. Compiler basically performs tail recursion optimization, removing stack implementation.Consider below code.

void tail(int i) {
    if(i<=0) return;
    else {
     system.out.print(i+"");
     tail(i-1);
    }
   }

After performing optimization , the above code is converted into below one.

void tail(int i) {
    blockToJump:{
    if(i<=0) return;
    else {
     system.out.print(i+"");
     i=i-1;
     continue blockToJump;  //jump to the bolckToJump
    }
    }
   }

This is how compiler does Tail Recursion Optimization.

Annettannetta