Why are epsilon transitions used in NFA?

Question

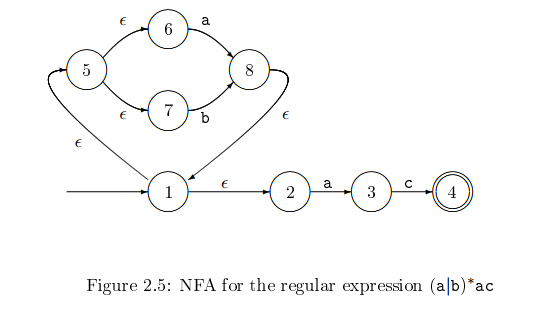
I'm trying to understand how to create NFA-s from regular expressions, but I am really confused from epsilon transitions. I have this example in my textbook , but I don't understand why epsilon transitions are used and how does one know when to use them.

Transvestite

Answer 1

In general, espilon-transitions are used when they are convenient. For example, when constructing an NFA from a regular expression, you start by constructing small parts of the automaton corresponding to parts of the expression. To connect them, you need to put a transition. But if there is no symbol to be read there, an epsilon transition is a simple way to do this. They are, however never necessary, you can always find a solution without them.

In your example, just apply the algorithm described in your textbook. It tells you when to use them.

The epsilon transitions

• from 1 to 2 probably connects the parts for (a|b)* and for ac
• 1->5 and 8->1 probably result from the *
• 5->6 and 5->7 probably result from the alternative in |

Ectoparasite

Answer 2

Epsilon-transitions in NFAs are a natural representation of choice or disjunction or union in regular expressions. That is, a regular expression like r + s (or r | s or r U s depending on your preferred notation) is naturally represented as an NFA consisting of two independent NFAs, one for r and one for s, joined using e-transitions as follows:

          e
----->q0----->(r)
      |
      | e
      |
      V
     (s)

When used to connect states in more complicated ways, the effect may not be as easy or natural to describe, but essentially these transitions let you choose unconditionally among multiple options. So, if I have seen a part of the input already and there are a few different ways the string could end, I can represent that by using e-transitions to states that handle the different possibilities.

In your example, the e-transitions are not really serving any very useful function and are merely artifacts of the conversion algorithm you have used. That algorithm includes them because, in the general case, they may be useful or necessary. In your specific case this was not true, so they look out of place.

Sociology