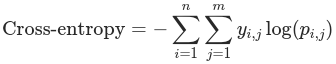How do I calculate cross-entropy from probabilities in PyTorch?

Question

By default, PyTorch's cross_entropy takes logits (the raw outputs from the model) as the input. I know that CrossEntropyLoss combines LogSoftmax (log(softmax(x))) and NLLLoss (negative log likelihood loss) in one single class. So, I think I can use NLLLoss to get cross-entropy loss from probabilities as follows:

true labels: [1, 0, 1]
probabilites: [0.1, 0.9], [0.9, 0.1], [0.2, 0.8]

where, y_i,j denotes the true value i.e. 1 if sample i belongs to class j and 0 otherwise. and p_i,j denotes the probability predicted by your model of sample i belonging to class j.

If I calculate by hand, it turns out to be:

>>> -(math.log(0.9) + math.log(0.9) + math.log(0.8))
0.4338

Using PyTorch:

>>> labels = torch.tensor([1, 0, 1], dtype=torch.long)
>>> probs = torch.tensor([[0.1, 0.9], [0.9, 0.1], [0.2, 0.8]], dtype=torch.float)
>>> F.nll_loss(torch.log(probs), labels)
tensor(0.1446)

What am I doing wrong? Why is the answer different?

Fenestra

Answer 1

There is a reduction parameter for all loss functions in the PyTorch. As you can see from the documentation default reduction parameter is 'mean' which divides the sum with number of elements in the batch. To get a summation behavior (0.4338) as you want, you should give the reduction parameter as following:

F.nll_loss(torch.log(probs), labels,reduction='sum')

Buckish