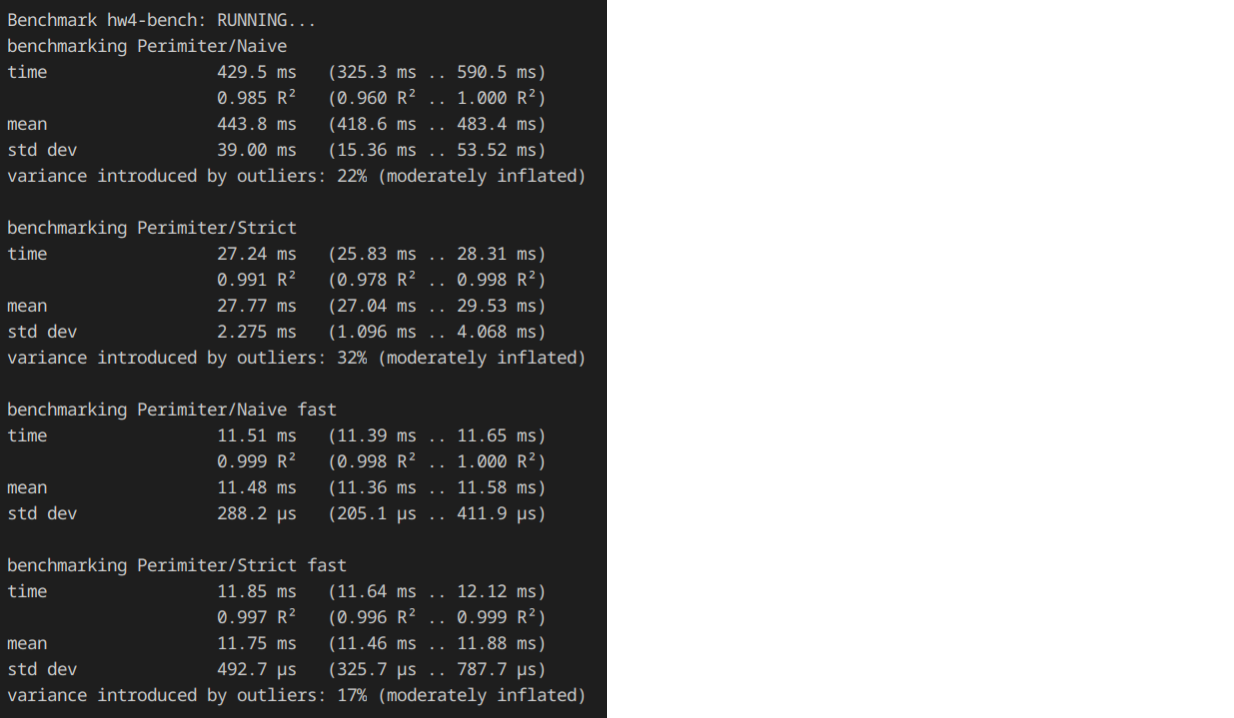
I have several different implementations of the same function. The difference lies in the use of bang patterns. The question is, why does perimeterNaiveFast work the same as perimeterStrictFast?
Function realisations:
> data Point = Point { x :: Int, y :: Int }
>
> distance :: Point -> Point -> Double
> distance (Point x1 y1) (Point x2 y2) =
> sqrt $ fromIntegral $ (x1 - x2) ^ (2 :: Int) + (y1 - y2) ^ (2 :: Int)
>
> perimeterNaive :: [Point] -> Double
> perimeterNaive [] = 0.0
> perimeterNaive points = foldPoints points 0.0
> where
> firstPoint = head points
> foldPoints [] _ = 0.0
> foldPoints [lst] acc = acc + distance firstPoint lst
> foldPoints (prev:next:rst) acc = foldPoints (next:rst) (acc + distance prev next)
>
> perimeterStrict :: [Point] -> Double perimeterStrict [] = 0.0
> perimeterStrict points = foldPoints points 0.0
> where
> firstPoint = head points
> foldPoints [] _ = 0.0
> foldPoints [lst] acc = acc + distance firstPoint lst
> foldPoints (prev:next:rst) !acc = foldPoints (next:rst) (acc + distance prev next)
>
> perimeterNaiveFast :: [Point] -> Double perimeterNaiveFast [] = 0.0
> perimeterNaiveFast (first:rest) = foldPoints rest first 0.0
> where
> foldPoints [] lst acc = acc + distance first lst
> foldPoints (next:rst) prev acc = foldPoints rst next (acc + distance next prev)
>
> perimeterStrictFast :: [Point] -> Double perimeterStrictFast [] = 0.0
> perimeterStrictFast (first:rest) = foldPoints rest first 0.0
> where
> foldPoints [] lst acc = acc + distance first lst
> foldPoints (next:rst) prev !acc = foldPoints rst next (acc + distance next prev)
>
> main :: IO ()
> main = defaultMain [ perimeterBench $ 10 ^ (6 :: Int) ]
>
> perimeterBench :: Int -> Benchmark perimeterBench n = bgroup "Perimiter"
> [ bench "Naive" $ nf perimeterNaive points
> , bench "Strict" $ nf perimeterStrict points
> , bench "Naive fast" $ nf perimeterNaiveFast points
> , bench "Strict fast" $ nf perimeterStrictFast points
> ]
> where
> points = map (\i -> Point i i) [1..n]