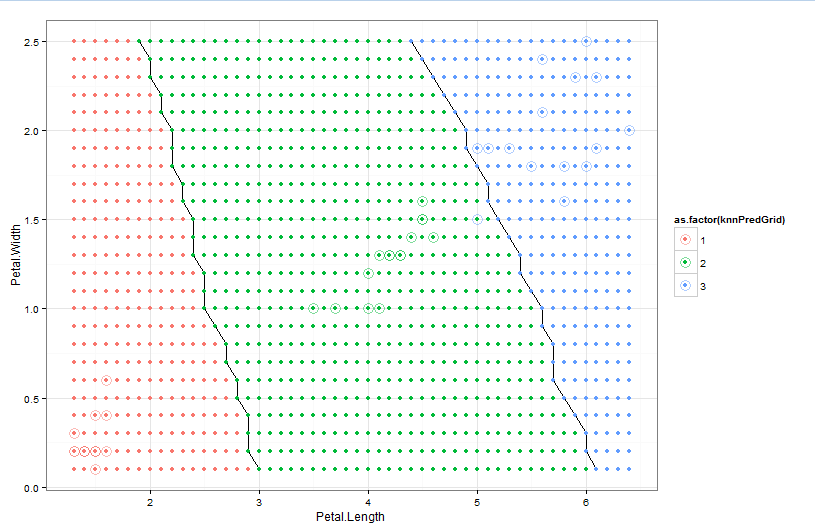
I'd like to plot a decision boundary for the model created by the Caret package. Ideally, I'd like a general case method for any classifier model from Caret. However, I'm currently working with the kNN method. I've included code below that uses the wine quality dataset from UCI which is what I'm working with right now.
I found this method that works with the generic kNN method in R, but can't figure out how to map it to Caret -> https://stats.stackexchange.com/questions/21572/how-to-plot-decision-boundary-of-a-k-nearest-neighbor-classifier-from-elements-o/21602#21602
library(caret)
set.seed(300)
wine.r <- read.csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-red.csv', sep=';')
wine.w <- read.csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-white.csv', sep=';')
wine.r$style <- "red"
wine.w$style <- "white"
wine <- rbind(wine.r, wine.w)
wine$style <- as.factor(wine$style)
formula <- as.formula(quality ~ .)
dummies <- dummyVars(formula, data = wine)
dummied <- data.frame(predict(dummies, newdata = wine))
dummied$quality <- wine$quality
wine <- dummied
numCols <- !colnames(wine) %in% c('quality', 'style.red', 'style.white')
low <- wine$quality <= 6
high <- wine$quality > 6
wine$quality[low] = "low"
wine$quality[high] = "high"
wine$quality <- as.factor(wine$quality)
indxTrain <- createDataPartition(y = wine[, names(wine) == "quality"], p = 0.7, list = F)
train <- wine[indxTrain,]
test <- wine[-indxTrain,]
corrMat <- cor(train[, numCols])
correlated <- findCorrelation(corrMat, cutoff = 0.6)
ctrl <- trainControl(
method="repeatedcv",
repeats=5,
number=10,
classProbs = T
)
t1 <- train[, -correlated]
grid <- expand.grid(.k = c(1:20))
knnModel <- train(formula,
data = t1,
method = 'knn',
trControl = ctrl,
tuneGrid = grid,
preProcess = 'range'
)
t2 <- test[, -correlated]
knnPred <- predict(knnModel, newdata = t2)
# How do I render the decision boundary?