Issue checking if binary tree is also binary search tree

Question

I'm trying to solve this problem but I'm having some troubles:

In a binary search tree (BST):

• The data value of every node in a node's left subtree is less than the data value of that node.
• The data value of every node in a node's right subtree is greater than the data value of that node.

Given the root node:

class Node {
    int data;
    Node left;
    Node right;
}

Determine if the binary tree is also a binary search tree

I have this code:

boolean check(Node root) {   

    //node doesn't have any children
    if (root.left == null && root.right == null) {
        return true;
    }

    boolean leftIsBst = true;
    boolean rightIsBst = true;

    if (root.left != null) {
        leftIsBst = (root.left.data < root.data) && check(root.left);
    }

    if (root.right != null) {
        rightIsBst = (root.right.data > root.data) && check(root.right);
    }

    return leftIsBst && rightIsBst;
}

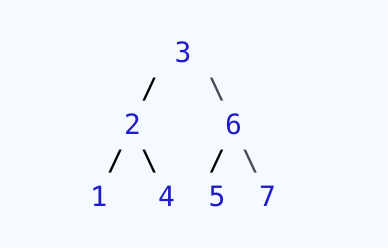
This is working in some cases, but it fails in cases like this one:

As you see, node (4) is in the node (3)'s left subtree, although 4 is greater than 3, so the method should return false. My code returns true, though.

How could I control that case? How can I check that all the values in the left/right subtree are lower/greater than the root (not only the direct child)?

Rabbi

Answer 1

Your definitions are correct (although you don't necessarily need to insist that all the keys are distinct), but your code doesn't implement all the conditions in your definitions. Specifically, you don't enforce the minimum and maximum values in each subtree.

Here is an efficient recursive solution that implements your definitions:

boolean check(Node root) {
    return check(root, INT_MIN, INT_MAX);
}
boolean check(Node n, int minval, int maxval) {
    if (n == null) {
        return true;
    }
    return (
        n.data >= minval && n.data <= maxval &&
        check(n.left, minval, n.data-1) &&
        check(n.right, n.data+1, maxval)
    );
}

Note that I didn't bother checking for overflow in n.data-1 and n.data+1, which you would have to do in real life. If you want to allow duplicate keys, just change these to n.data and you don't have to worry about it.

Dunne

Omg this is crazy, it's working like a charm and it's so simple... Thank you! – Sadowski

Answer 2

Something like the following should work

boolean check(Node root) {   

    if (root == null) {
        return true;
    }


    if (root.left != null && max(root.left) > root.data  ) {
        return false
    }

    if (root.right != null && max(root.right) < root.data ) {
        return false;
    }

    return check(root.left) && check(root.right);
}

Note:

• this is fairly inefficient
• you need to implement max()

Glob

The solution by Matt Timmermans is conceptually the same but is much more efficient. – Glob

I have tested your solution and it's working but you're right, it's not that efficient. Thank you anyway! +1 – Sadowski

Yup, that max logic is expensive. – Glob

Answer 3

Your recursion logic is not proper. I am giving here cpp logic. You may need to translate it to Java code.

bool check(Node *root) {

static Node *prev = NULL;

if(root) {

    If(!check(root->left)) return false;

    If(prev != Null && prev->data > root->data) return false;

    Prev = root;

    return check(root->right);


}

return true;

}

Loxodromic

Just replace NULL with null, remove the asterisk and replace -> with a dot. And you have your java code – Intrench

People are giving -1 for no reason. we are disregarding stackoverflow's intention to help people resolve their problem. I am greatly disappointed by the people's response to my answer. Isn't this the solution to the question he has asked, won't it lead to the answer he is expecting. – Loxodromic

This is obscure code. Even though it works, one would not learn much by having it. Would be better if you provided explanations on what prev stands for. – Kushner

Answer 4

A BST is defined as:

-The left subtree of a node always contains nodes with values less than that of the node. - The right subtree of a node always contains nodes with values greater than that of the node. -Both left and right sub trees are also valid BSTs.

    class Solution {
        public boolean isValidBST(TreeNode root) {
            return helper (root,Integer.MIN_VALUE,Integer.MAX_VALUE);
        }
        public boolean helper(TreeNode root,long low,long high){
            if (root==null){
                return true;
            }
            if (root.val<low ||root.val>high){
                return false;
            }
            return (helper(root.left,low,root.val-1) && 
    helper(root.right,root.val+1,high));
        }
    }

Henriettehenriha