Algorithm for miter joins on multiple lines

Question

In order to draw, for instance, roads or walls, we know how to calculate a miter join on 2 connecting lines, resulting in something like this

But is there an algorithm to efficiently calculate points for a nice join when 3 or more lines connect to the same point, like this

The input is a list of segments

NB: The ultimate goal is to triangulate this

Acroter

Answer 1

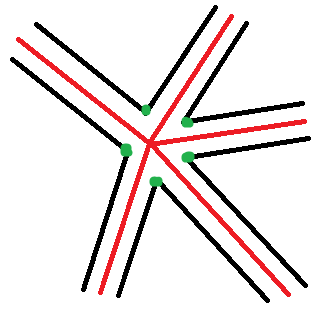
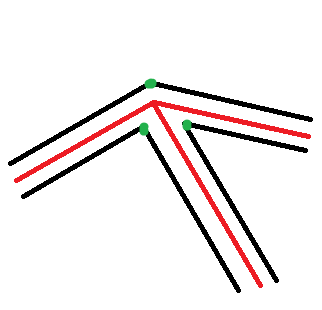
Let's say your segments (in red) join in the origin of your cartesian coordinates system. Identify your segments by their angle from an axis of your choice, let's say the x axis. Draw the walls (in black) around the segment, let's say they have both different width from the red segment, t₁ and t₂.

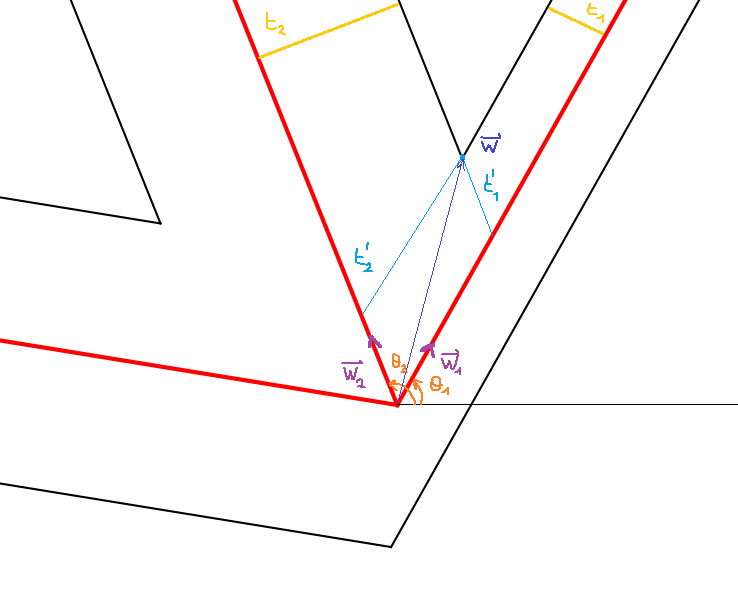
Now the idea is to find the coordinates of your intersection vector. As you can see, a rhombus immediatly emerges from this geometry. Doing a bit of vector calculation gets you easily to the answer.

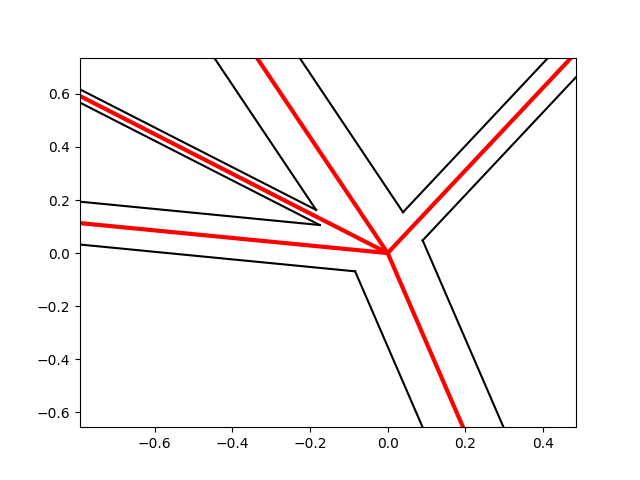
Here is a little Python script for illustration, using MatPlotLib:

import matplotlib.pyplot as plt
import math

angles = [1.0, 2.0, 2.5, 3.0, 5.0] # list of angles corresponding to your red segments (middle of your walls)
wall_len = [0.05, 0.1, 0.02, 0.08, 0.1] # list of half-width of your walls
nb_walls = len(angles)

for a in angles:
    plt.plot((0, math.cos(a)), (0, math.sin(a)), "r", linewidth=3) # plotting the red segments

for i in range(0, len(angles)):
    j = (i + 1)%nb_walls
    angle_n = angles[i] # get angle Θ_n
    angle_np = angles[j] # get the angle Θ_n+1 (do not forget to loop to the first angle when you get to the last angle in the list)
    wall_n = wall_len[i] # get the thickness of the n-th wall t_n
    wall_np = wall_len[j] # get the thickness of the n+1-th wall t_n+1
    dif_angle = angle_np - angle_n # ΔΘ
    t1 = wall_n/math.sin(dif_angle) # width of the rhombus
    t2 = wall_np/math.sin(dif_angle) # height of the rhombus

    x = t2*math.cos(angle_n) + t1*math.cos(angle_np) # x coordinates of the intersection point
    y = t2*math.sin(angle_n) + t1*math.sin(angle_np) # y coordinates of the intersection point

    wall_n = [math.cos(angle_n), math.sin(angle_n)] # for plotting n-th wall
    wall_np = [math.cos(angle_np), math.sin(angle_np)] # for plotting n+1-th wall

    plt.plot((x, wall_n[0] + x), (y, wall_n[1] + y), "k") # plotting the n wall
    plt.plot((x, wall_np[0] + x), (y, wall_np[1] + y), "k") # plotting the n+1 wall

plt.show()

Snuff

Awesome answer, very well documented and explained ! This really helps ! – Acroter