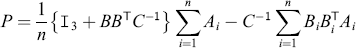Generalisation of the “mid-point” method for triangulation to n points

Question

In Computer Vision the "mid-point" method solves the triangulation problem of determining a 3D point from two 2D points (see here). Is there a generalisation of this to more than two points, say n points, and what is it called? The article does mention Direct Linear Transformation, but I'm not sure this is what I'm looking for...

Breakup

Answer 1

Yes there is a generalisation to N points. I have saw it in some articles:

P. A. Beardsley, A. Zisserman, and D. W. Murray. Sequential updating of projective and affine structure from motion. Int. J. Comput. Vision, 23(3) :235–259, June 1997

Srikumar Ramalingam, Suresh K. Lodha, and Peter Sturm. A generic structure- from-motion framework. Comput. Vis. Image Underst., 103(3) :218–228, September 2006.

You can also read the book (the refererence of your wikipedia article)

Richard Hartley and Andrew Zisserman (2003). Multiple View Geometry in computer vision. Cambridge University Press. ISBN 978-0-521-54051-3.

But it do not mention the midpoint for N views as I remember, only for two views while this method is depicted as innacurate (Not strictly my thinking).

I hope it will be helpful.

Scherzando

Thank you. In the end I worked out the equations myself and solved the problem. – Breakup

Answer 2

As Fleurmond suggested, the generalisation of midpoint triangulation to n-views is given in:

Srikumar Ramalingam, Suresh K. Lodha, and Peter Sturm. A generic structure- from-motion framework. Comput. Vis. Image Underst., 103(3) :218–228, September 2006

Here is a sample code in Python:

import numpy as np
import numpy.linalg as npla

def midpoint_triangulate(x, cam):
    """
    Args:
        x:   Set of 2D points in homogeneous coords, (3 x n) matrix
        cam: Collection of n objects, each containing member variables
                 cam.P - 3x4 camera matrix
                 cam.R - 3x3 rotation matrix
                 cam.T - 3x1 translation matrix
    Returns:
        midpoint: 3D point in homogeneous coords, (4 x 1) matrix
    """

    n = len(cam)                                         # No. of cameras

    I = np.eye(3)                                        # 3x3 identity matrix
    A = np.zeros((3,n))
    B = np.zeros((3,n))
    sigma2 = np.zeros((3,1))

    for i in range(n):
        a = -np.transpose(cam[i].R).dot(cam[i].T)        # ith camera position
        A[:,i,None] = a

        b = npla.pinv(cam[i].P).dot(x[:,i])              # Directional vector
        b = b / b[3]
        b = b[:3,None] - a
        b = b / npla.norm(b)
        B[:,i,None] = b

        sigma2 = sigma2 + b.dot(b.T.dot(a))

    C = (n * I) - B.dot(B.T)
    Cinv = npla.inv(C)
    sigma1 = np.sum(A, axis=1)[:,None]
    m1 = I + B.dot(np.transpose(B).dot(Cinv))
    m2 = Cinv.dot(sigma2)

    midpoint = (1/n) * m1.dot(sigma1) - m2        
    return np.vstack((midpoint, 1))

Expugnable