Using StatsModels to plot quantile regression for 2nd order polynomial

Question

I am following the StatsModels example here to plot quantile regression lines. With only slight modification for my data, the example works great, producing this plot (note that I have modified the code to only plot the 0.05, 0.25, 0.5, 0.75, and 0.95 quantiles) :

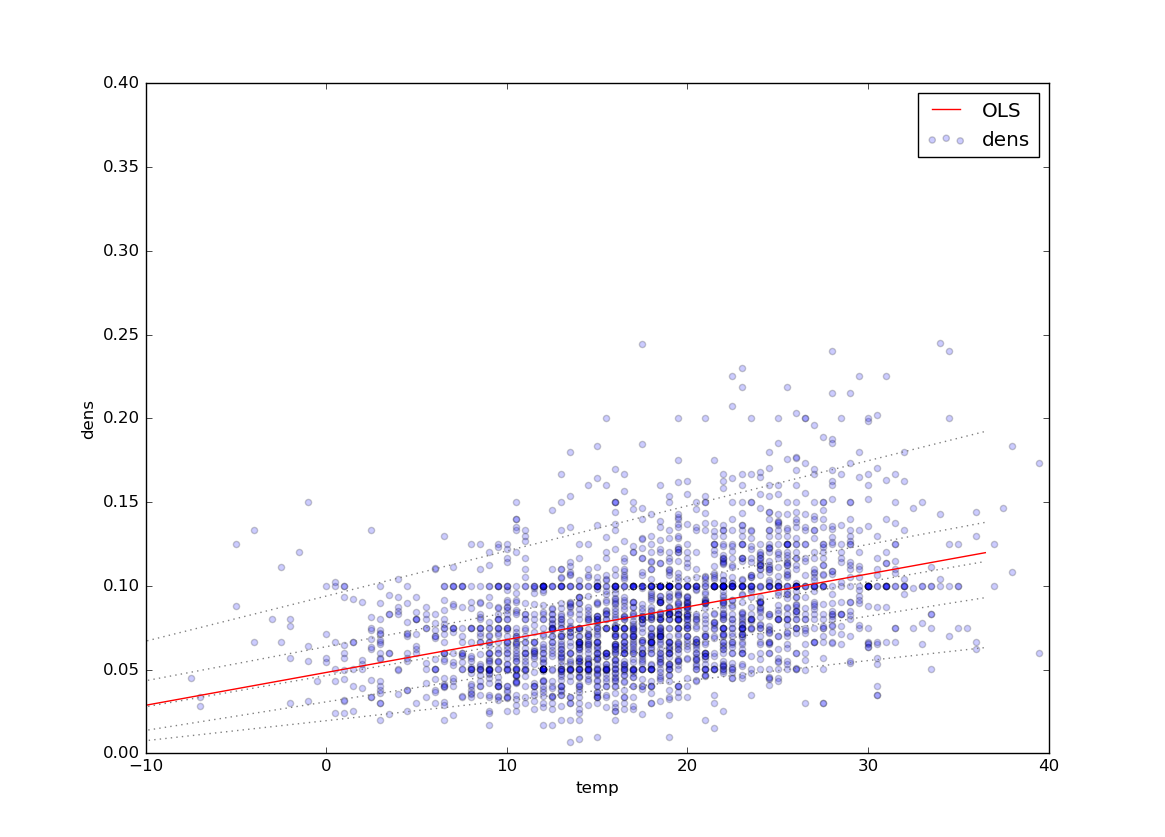
However, I would like to plot the OLS fit and corresponding quantiles for a 2nd order polynomial fit (instead of linear). For example, here is the 2nd-order OLS line for the same data:

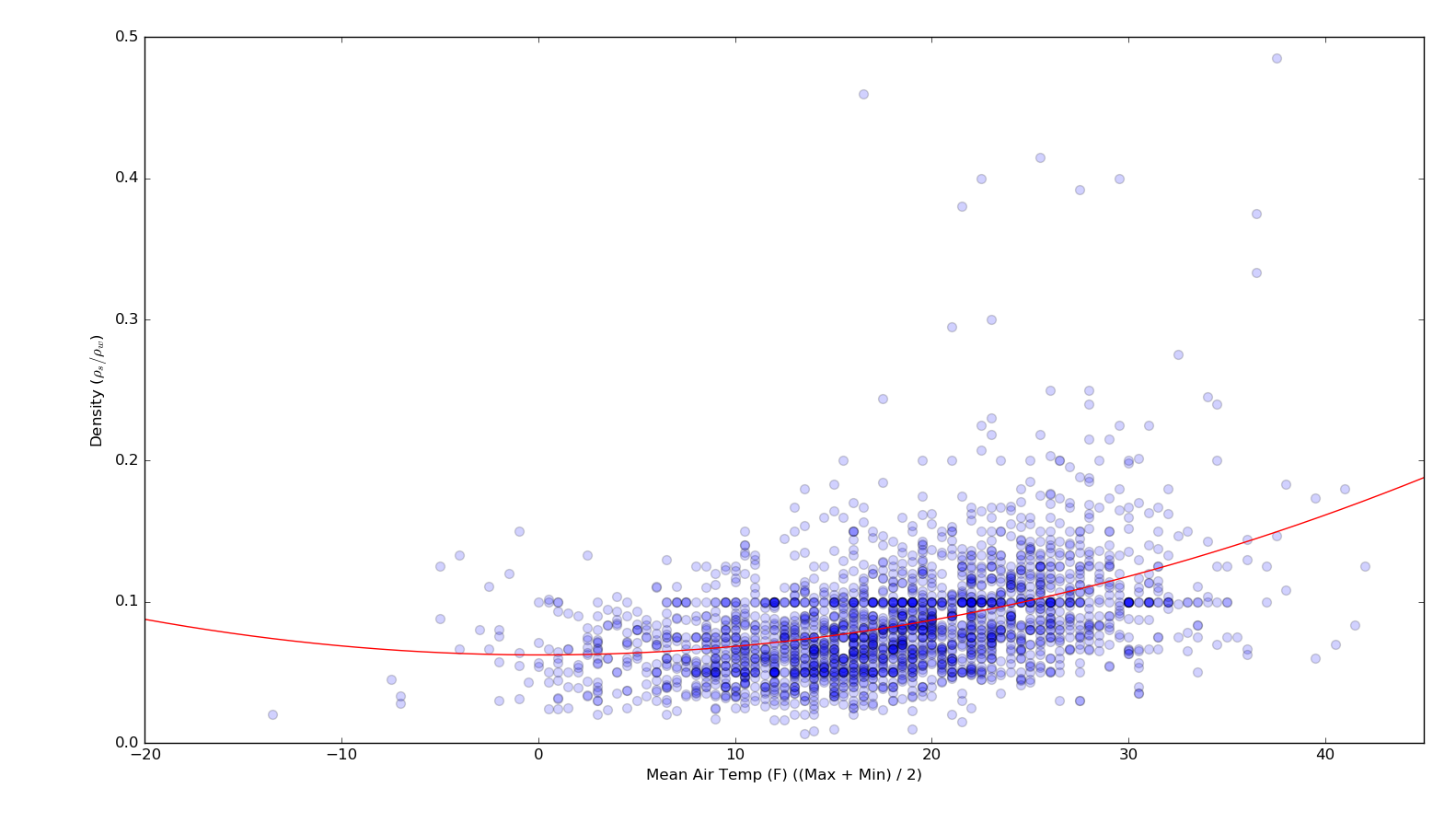
How can I modify the code in the linked example to produce non-linear quantiles?

Here is my relevant code modified from the linked example to produce the 1st plot:

d = {'temp': x, 'dens': y}
df = pd.DataFrame(data=d)

# Least Absolute Deviation
# 
# The LAD model is a special case of quantile regression where q=0.5

mod = smf.quantreg('dens ~ temp', df)
res = mod.fit(q=.5)
print(res.summary())

# Prepare data for plotting
# 
# For convenience, we place the quantile regression results in a Pandas DataFrame, and the OLS results in a dictionary.

quantiles = [.05, .25, .50, .75, .95]
def fit_model(q):
    res = mod.fit(q=q)
    return [q, res.params['Intercept'], res.params['temp']] + res.conf_int().ix['temp'].tolist()

models = [fit_model(x) for x in quantiles]
models = pd.DataFrame(models, columns=['q', 'a', 'b','lb','ub'])

ols = smf.ols('dens ~ temp', df).fit()
ols_ci = ols.conf_int().ix['temp'].tolist()
ols = dict(a = ols.params['Intercept'],
           b = ols.params['temp'],
           lb = ols_ci[0],
           ub = ols_ci[1])

print(models)
print(ols)

x = np.arange(df.temp.min(), df.temp.max(), 50)
get_y = lambda a, b: a + b * x

for i in range(models.shape[0]):
    y = get_y(models.a[i], models.b[i])
    plt.plot(x, y, linestyle='dotted', color='grey')

y = get_y(ols['a'], ols['b'])
plt.plot(x, y, color='red', label='OLS')

plt.scatter(df.temp, df.dens, alpha=.2)
plt.xlim((-10, 40))
plt.ylim((0, 0.4))
plt.legend()
plt.xlabel('temp')
plt.ylabel('dens')
plt.show()

Shawana

Answer 1

After a day of looking into this, came up with a solution, so posting my own answer. Much credit to Josef Perktold at StatsModels for assistance.

Here is the relevant code and plot:

d = {'temp': x, 'dens': y}
df = pd.DataFrame(data=d)

x1 = pd.DataFrame({'temp': np.linspace(df.temp.min(), df.temp.max(), 200)})

poly_2 = smf.ols(formula='dens ~ 1 + temp + I(temp ** 2.0)', data=df).fit()
plt.plot(x, y, 'o', alpha=0.2)
plt.plot(x1.temp, poly_2.predict(x1), 'r-', 
         label='2nd order poly fit, $R^2$=%.2f' % poly_2.rsquared, 
         alpha=0.9)
plt.xlim((-10, 50))
plt.ylim((0, 0.25))
plt.xlabel('mean air temp')
plt.ylabel('density')
plt.legend(loc="upper left")


# with quantile regression

# Least Absolute Deviation
# The LAD model is a special case of quantile regression where q=0.5

mod = smf.quantreg('dens ~ temp + I(temp ** 2.0)', df)
res = mod.fit(q=.5)
print(res.summary())

# Quantile regression for 5 quantiles

quantiles = [.05, .25, .50, .75, .95]

# get all result instances in a list
res_all = [mod.fit(q=q) for q in quantiles]

res_ols = smf.ols('dens ~ temp + I(temp ** 2.0)', df).fit()


plt.figure()

# create x for prediction
x_p = np.linspace(df.temp.min(), df.temp.max(), 50)
df_p = pd.DataFrame({'temp': x_p})

for qm, res in zip(quantiles, res_all):
    # get prediction for the model and plot
    # here we use a dict which works the same way as the df in ols
    plt.plot(x_p, res.predict({'temp': x_p}), linestyle='--', lw=1, 
             color='k', label='q=%.2F' % qm, zorder=2)

y_ols_predicted = res_ols.predict(df_p)
plt.plot(x_p, y_ols_predicted, color='red', zorder=1)
#plt.scatter(df.temp, df.dens, alpha=.2)
plt.plot(df.temp, df.dens, 'o', alpha=.2, zorder=0)
plt.xlim((-10, 50))
plt.ylim((0, 0.25))
#plt.legend(loc="upper center")
plt.xlabel('mean air temp')
plt.ylabel('density')
plt.title('')
plt.show()

red line: 2nd order polynomial fit

black dashed lines: 5th, 25th, 50th, 75th, 95th percentiles

Shawana

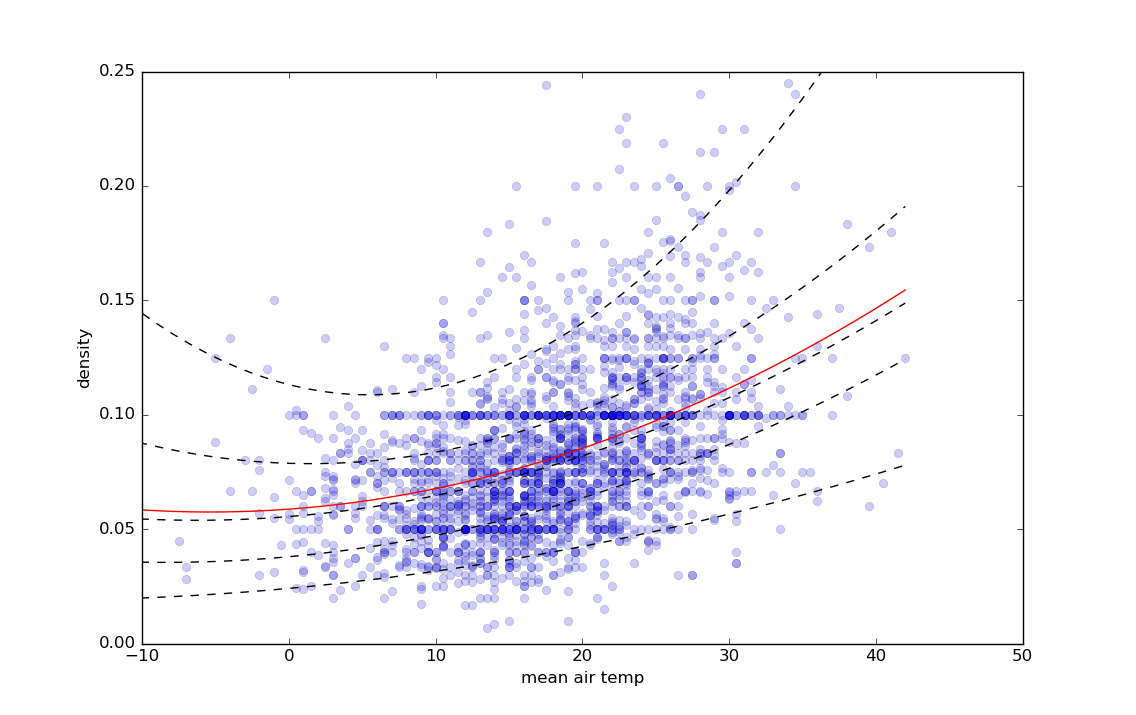
Can you please clarify what the purpose of "I" in the model is? 'dens ~ temp + I(temp ** 2.0)' – Eberhard

This is syntax used for Patsy (a formula "mini-language"). See patsy.readthedocs.io/en/v0.1.0/API-reference.html#. (x ** 2.0) doesn't work in a formula, you need the I so patsy doesn't try to make a transformation designed for categorical. – Shawana

Should I worry about FutureWarning: Using a non-tuple sequence for multidimensional indexing is deprecated; use `arr[tuple(seq)]` instead of `arr[seq]`. In the future this will be interpreted as an array index, `arr[np.array(seq)]`, which will result either in an error or a different result. ? – Inactivate

I'm not sure what part of the code is throwing this warning... something within the StatsModels package? But yes, this looks like it is probably worth paying attention to. If it is in your own code, maybe some simple modifications can address the warning. If it is in StatsModels, it may need to be brought to the attention of the StatsModels developers. – Shawana