Creating a Binary Search Tree from a sorted array

Question

I am currently checking about coding an algorithms. If we have the following case:

Given a sorted (increasing order) array with unique integer elements, wrote an algorithm to create a binary search tree with minimal height.

The following code is proposed as the solution:

TreeNode createMinimalBST(int arr[], int start, int end){
    if (end < start) {
        return null;
    }
    int mid = (start + end) / 2;
    TreeNode n = new TreeNode(arr[mid]);
    n.setLeftChild(createMinimalBST(arr, start, mid - 1));
    n.setRightChild(createMinimalBST(arr, mid + 1, end));
    return n;
}

TreeNode createMinimalBST(int array[]) {
    return createMinimalBST(array, 0, array.length - 1);
}

But if I try this code with the following array input:

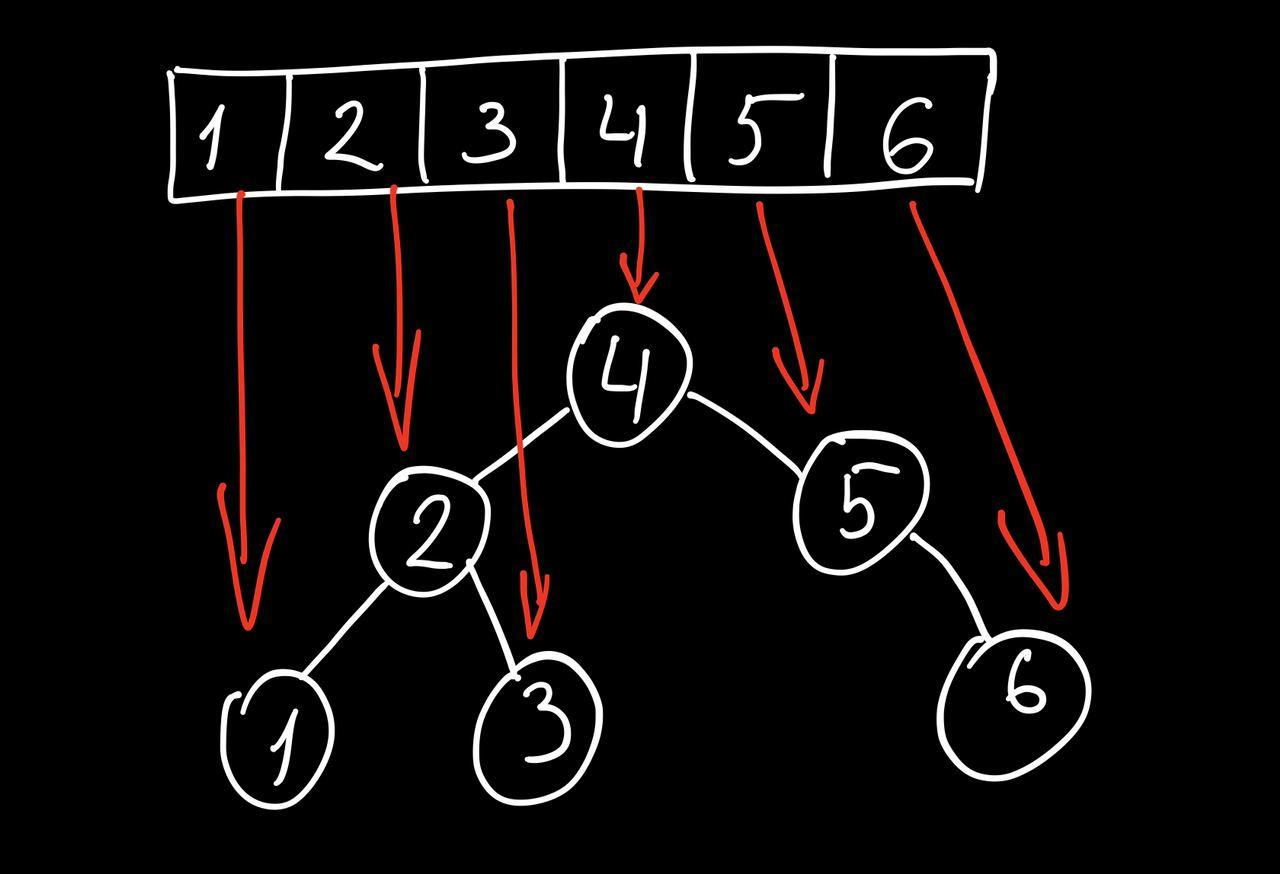
[2,4,6,8,10,20]

And I perform the first iteration

createMinimalBST([2,4,6,8,10,20], 0, 5);

The following line:

int mid = (start + end) / 2; // in Java (0 + 5) / 2  =  2;

would calculate the mid as the root of the binary search tree the position number 2 which is the value 6.

However, the binary search tree in this example should look like:

    8
   / \
  4   10
 / \    \
2   6   20 

The code is coming from a reputable source, but my gut feeling is that the implementation is incorrect.

Am I missing something or the implementation is not right ?

Presume

end should be the length of your array. is it? – Apraxia

the value of end is correct in the code (according to the solution provided) array.length - 1 – Presume

You can modify the formula to calculate mid. If end-start+1 is odd, the mid = (start+end)/2, otherwise mid = (start + end)/2 + 1. Moreover, can you please share the link of the source ? – Sputum

@GAURANGVYAS The source is a book called Cracking the Coding Interview (6th edition). The solution is on page 242. – Presume

Answer 1

Reference GeeksForGeeks

Algorithm -

1. Get the Middle of the array and make it root.
2. Recursively do same for left half and right half.
   • Get the middle of left half and make it left child of the root created in step 1.
   • Get the middle of right half and make it right child of the root created in step 1.

Wikipedia Link

CODE

 class Node {

    int data;
    Node left, right;

    Node(int d) {
        data = d;
        left = right = null;
    }
}

class BinaryTree {

    static Node root;

    /* A function that constructs Balanced Binary Search Tree 
    from a sorted array */
    Node sortedArrayToBST(int arr[], int start, int end) {

        /* Base Case */
        if (start > end) {
            return null;
        }

        /* Get the middle element and make it root */
        int mid = (start + end) / 2;
        Node node = new Node(arr[mid]);

        /* Recursively construct the left subtree and make it
        left child of root */
        node.left = sortedArrayToBST(arr, start, mid - 1);

        /* Recursively construct the right subtree and make it
        right child of root */
        node.right = sortedArrayToBST(arr, mid + 1, end);

        return node;
    }

    /* A utility function to print preorder traversal of BST */
    void preOrder(Node node) {
        if (node == null) {
            return;
        }
        System.out.print(node.data + " ");
        preOrder(node.left);
        preOrder(node.right);
    }

    public static void main(String[] args) {
        BinaryTree tree = new BinaryTree();
        int arr[] = new int[]{2, 4, 6, 8, 10, 12};
        int n = arr.length;
        root = tree.sortedArrayToBST(arr, 0, n - 1);
        System.out.println("Preorder traversal of constructed BST");
        tree.preOrder(root);
    }
}

Houseroom

thanks for the response but I believe that the code is still picking up 6 as the root of the tree rather than 8. If the root starts by 6 it is not a binary search tree – Presume

@Presume If the root starts by 6 it is not a binary search tree- that's incorrect. It will be a balanced binary search irrespective of the fact that the root is 6 or 8. – Sputum

@GAURANGVYAS I have double checked and it works. There are several binary search tree that can be generated. Thanks for your help. – Presume

Looks like you forgot to remove the pre order traversal after copy-pasting from GeeksforGeeks. -1 for not attributing your source. – Embarrass

Wrote this answer way back; at that point of time I didn't realize the importance of giving credits to folks, but now i do; added the reference and thanks for the heads up – Houseroom

Answer 2

A sorted array will give you a balanced binary tree. This could be done easily in O(n) time, as we can get the middle element in O(1) time. Following is a simple algorithm,

1. Construct a node for the middle element in the array and return it (this will be the root in the base case).

   2. Repeat from 1. on the left half of the array, assigning the return value to the left child of the root.

   3. Repeat from 1. on the right half of the array, assigning the return value to the right child of the root.

Java implementation

 TreeNode sortedArrayToBST(int arr[], int start, int end) {  
           if (start > end)
              return null; // same as (start+end)/2, avoids overflow.    
           int mid = start + (end - start) / 2;      
           TreeNode node = new
           TreeNode(arr[mid]); 
           node.left = sortedArrayToBST(arr, start, mid-1); 
           node.right = sortedArrayToBST(arr, mid+1, end); 
            return node; 
    }

TreeNode sortedArrayToBST(int arr[]) { return sortedArrayToBST(arr, 0, arr.length-1); }

Time Complexity: ** O(n) ** Following is the recurrance relation for sortedArrayToBST().

T(n) = 2T(n/2) + C

T(n) --> Time taken for an array of size n

C --> Constant (Finding middle of array and linking root to left and right subtrees take constant time)

Chaetognath

You gave two answers and both of them are same. – Sputum

Not able to delete it. Will remove. – Chaetognath

@GAURANGVYAS if u can you delete the other 2, please do. – Chaetognath

Answer 3

• get the middle of the array and make it as root
• recursively do the same for the left half and the right half
  • get the middle of the left half and make it the left child of the root
  • get the middle of the right half and make it the right child of the root

    public TreeNode Convert(int[] array)
    {
        if (array == null || array.Length == 0)
        {
            return null;
        }

        return Convert(array, 0, array.Length - 1);
    }

    private static TreeNode Convert(int[] array, int lo, int hi)
    {
        if (lo > hi)
        {
            return null;
        }

        int mid = lo + (hi - lo) / 2;
        var root = new TreeNode(array[mid]);
        root.Left = Convert(array, lo, mid - 1);
        root.Right = Convert(array, mid + 1, hi);
        return root;
    }

Time Complexity: O(n)

from CodeStandard

Howdah