Calculating B spline basis in Matlab in the same way as R's bs() function

Question

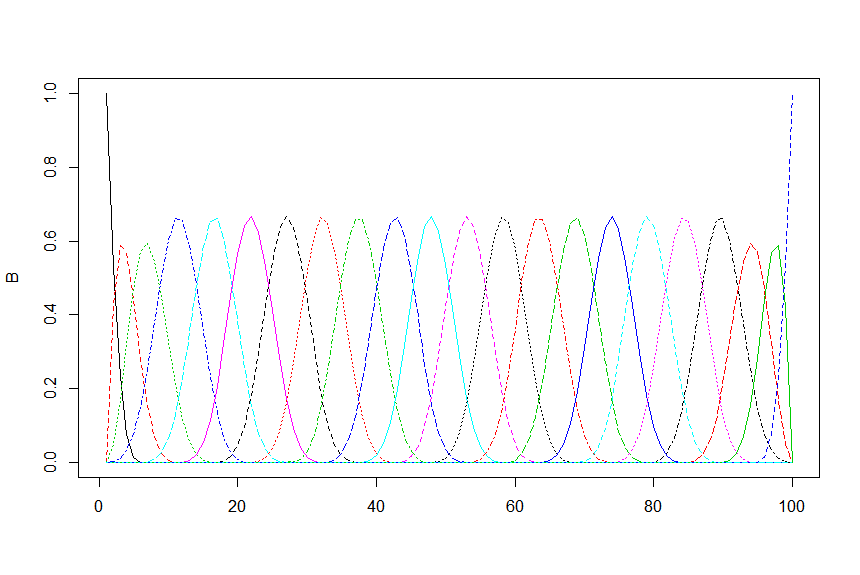
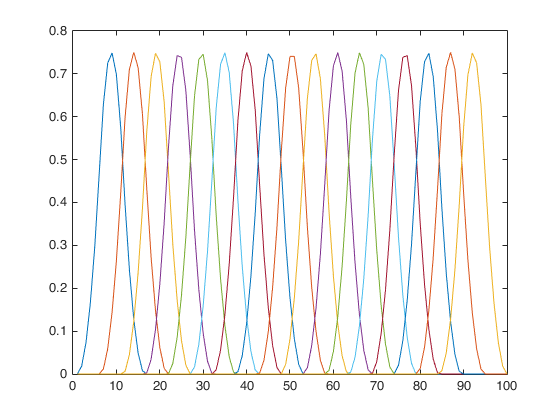
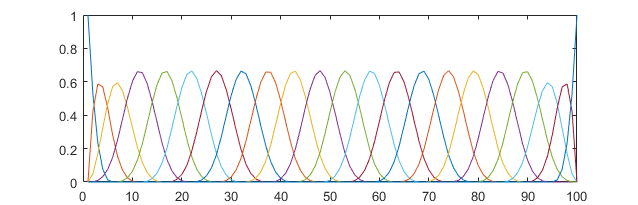
I am on the lookout for (an ideally inbuilt) function in Matlab that calculates a B spline basis matrix the same way as in R, e.g. for a spline basis with 20 equally spaced knots of degree 3, I would do in R

require(splines)
B = bs(x = seq(0,1,length.out=100),
        knots = seq(0, 1, length.out=20), # 20 knots
        degree = 3,
        intercept = FALSE)
matplot(B,type="l")

To get the same in Matlab I thought I could use

B = spcol(linspace(0,1,20),3,linspace(0,1,100));
plot(B);

but as can be seen the boundary knots then are missing. Any thoughts what would be the equivalent syntax in Matlab to get the same as in R?

PS The code that R is using for bs() is in somewhat simplified form:

basis <- function(x, degree, i, knots) {
  if(degree == 0){
    B <- ifelse((x >= knots[i]) & (x < knots[i+1]), 1, 0)
  } else {
    if((knots[degree+i] - knots[i]) == 0) {
      alpha1 <- 0
    } else {
      alpha1 <- (x - knots[i])/(knots[degree+i] - knots[i])
    }
    if((knots[i+degree+1] - knots[i+1]) == 0) {
      alpha2 <- 0
    } else {
      alpha2 <- (knots[i+degree+1] - x)/(knots[i+degree+1] - knots[i+1])
    }
    B <- alpha1*basis(x, (degree-1), i, knots) + alpha2*basis(x, (degree-1), (i+1), knots)
  }
  return(B)
}

bs <- function(x, degree=3, interior.knots=NULL, intercept=FALSE, Boundary.knots = c(0,1)) {
  if(missing(x)) stop("You must provide x")
  if(degree < 1) stop("The spline degree must be at least 1")
  Boundary.knots <- sort(Boundary.knots)
  interior.knots.sorted <- NULL
  if(!is.null(interior.knots)) interior.knots.sorted <- sort(interior.knots)
  knots <- c(rep(Boundary.knots[1], (degree+1)), interior.knots.sorted, rep(Boundary.knots[2], (degree+1)))
  K <- length(interior.knots) + degree + 1
  B.mat <- matrix(0,length(x),K)
  for(j in 1:K) B.mat[,j] <- basis(x, degree, j, knots)
  if(any(x == Boundary.knots[2])) B.mat[x == Boundary.knots[2], K] <- 1
  if(intercept == FALSE) {
    return(B.mat[,-1])
  } else {
    return(B.mat)
  }
}

Hengelo

Answer 1

Two things are going wrong in your code

1. I think there is some confusion here between degree and order. You correctly specified degree=3 in your R code, but in MATLAB the argument passed to spcol is the order of the spline. In general, a spline function of order n is a piecewise polynomial of degree n-1. [1]

   Because MATLAB's spcol accepts the order as an input, you need to specify order=4 rather than what you thought you'd done which is degree=3! You generated a quadratic spline in MATLAB, and a cubic spline in R.

2. It looks like the end knots in your R plot have non-singular multiplicity, by which I mean they are repeated. Making the end-points have multiplicity of degree+1 (in our case 4) means that their positions coincide with the control polygon, these are known as clamped knots. [2]

   In the R documentation for bs it states that the knots array contains the internal breakpoints. It looks like the boundary knots are defined to be clamped in your longer code sample, since they are repeated degree+1 times, on this line:

   knots <- c(rep(Boundary.knots[1], (degree+1)), interior.knots.sorted, rep(Boundary.knots[2], (degree+1)))
   

   This makes sense for clamped end-points, and backs up the earlier point about the use of the degree input.

   So our knots vector (with clamped end-points) in MATLAB should be:

   k = [0, 0, 0, linspace(0,1,20), 1, 1, 1]
   

---

Conclusion

Let's use order 4, and a knots vector with clamped knots at the end-points:

B = spcol([0, 0, 0, linspace(0,1,20), 1, 1, 1], 4, linspace(0,1,100)); 
plot(B);

We can now see the boundary knots like they are in the R plot, and the 2 additional peaks at each end which are smaller due to the influence of the degree 3 clamped knots.

---

Further reading

[1]: Wikipedia B-spline page

[2]: Useful page from MIT which describes clamped nodes and the mathematics in more depth.

Sissy