Why do compilers not coerce "n / 2.0" into "n * 0.5" if it's faster? [closed]

Question

I have always assumed that num * 0.5f and num / 2.0f were equivalent, since I thought the compiler was smart enough to optimize the division out. So today I decided to test that theory, and what I found out stumped me.

Given the following sample code:

float mul(float num) {
    return num * 0.5f;
}

float div(float num) {
    return num / 2.0f;
}

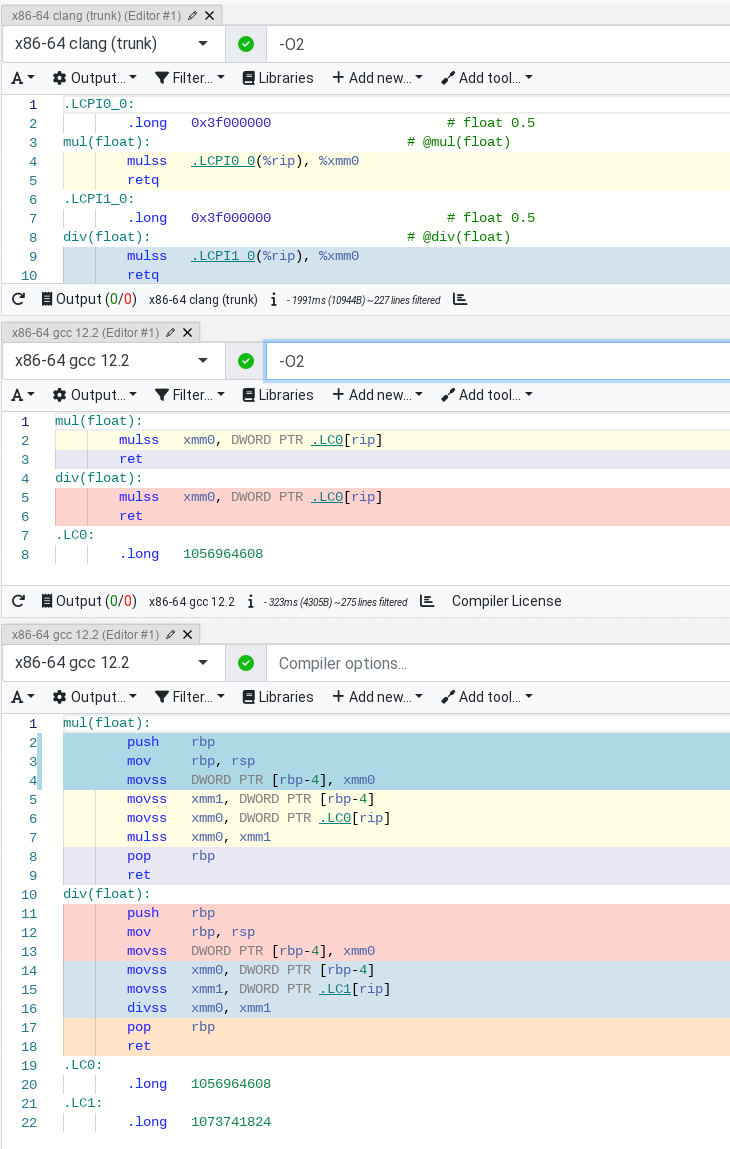
both x86-64 clang and gcc produce the following assembly output:

mul(float):
        push    rbp
        mov     rbp, rsp
        movss   DWORD PTR [rbp-4], xmm0
        movss   xmm1, DWORD PTR [rbp-4]
        movss   xmm0, DWORD PTR .LC0[rip]
        mulss   xmm0, xmm1
        pop     rbp
        ret
div(float):
        push    rbp
        mov     rbp, rsp
        movss   DWORD PTR [rbp-4], xmm0
        movss   xmm0, DWORD PTR [rbp-4]
        movss   xmm1, DWORD PTR .LC1[rip]
        divss   xmm0, xmm1
        pop     rbp
        ret

which when fed (looped) into the code analyzer available at https://uica.uops.info/ shows us the predicted throughput of 9.0 and 16.0 (skylake) cpu cycles respectively.

My question is: Why does the compiler not coerce the div function to be equivalent to the mul function? Surely having the rhs be a constant value should facilitate it, shouldn't it?

PS. I also tried out an equivalent example in Rust and the results ended up being 4.0 and 11.0 cpu cycles respectively.

Badderlocks

Try compiling with optimization enabled. – Velvavelvet

Because, contrary to popular (?) belief, every C++ compiler isn't made specifically for your CPU. – Adenine

godbolt.org/z/bTox76eYc they are optimized to be equivalent – Usage

@Adenine - huh? This optimization isn't target-specific, and divisions is much slower than multiplication on all CPUs. Compilers can (and do) do it in target-independent optimization passes, for divisors whose reciprocal is exactly representable as an IEEE float or double. (Or for any divisor with -ffast-math, rounding the reciprocal to nearest) – Insulate

I thought the compiler was smart enough to optimize the division out. Your thinking is correct. It appears you did not enable compiler optimizations. – Hydropathy

Basically a duplicate of Why does clang produce inefficient asm with -O0 (for this simple floating point sum)? , although Nole chose to post a more specific answer. There are other Q&As about compilers optimizing division to multiplication or not, but most of them aren't specific to / 2.0 which unlike most values has an exactly-representable reciprocal. Should I use multiplication or division? uses that example, but the answers aren't specific to ahead-of-time compiled langs or the power of 2. – Insulate

Answer 1

Both compilers will come down to the same implementation if you compile with -O2 optimized.

https://godbolt.org/z/v3dhvGref

Maloy