With scipy.stats.linregress I am performing a simple linear regression on some sets of highly correlated x,y experimental data, and initially visually inspecting each x,y scatter plot for outliers. More generally (i.e. programmatically) is there a way to identify and mask outliers?
Can scipy.stats identify and mask obvious outliers?
Asked Answered
The statsmodels package has what you need. Look at this little code snippet and its output:
# Imports #
import statsmodels.api as smapi
import statsmodels.graphics as smgraphics
# Make data #
x = range(30)
y = [y*10 for y in x]
# Add outlier #
x.insert(6,15)
y.insert(6,220)
# Make graph #
regression = smapi.OLS(x, y).fit()
figure = smgraphics.regressionplots.plot_fit(regression, 0)
# Find outliers #
test = regression.outlier_test()
outliers = ((x[i],y[i]) for i,t in enumerate(test) if t[2] < 0.5)
print 'Outliers: ', list(outliers)
Outliers: [(15, 220)]
Edit
With the newer version of statsmodels, things have changed a bit. Here is a new code snippet that shows the same type of outlier detection.
# Imports #
from random import random
import statsmodels.api as smapi
from statsmodels.formula.api import ols
import statsmodels.graphics as smgraphics
# Make data #
x = range(30)
y = [y*(10+random())+200 for y in x]
# Add outlier #
x.insert(6,15)
y.insert(6,220)
# Make fit #
regression = ols("data ~ x", data=dict(data=y, x=x)).fit()
# Find outliers #
test = regression.outlier_test()
outliers = ((x[i],y[i]) for i,t in enumerate(test.icol(2)) if t < 0.5)
print 'Outliers: ', list(outliers)
# Figure #
figure = smgraphics.regressionplots.plot_fit(regression, 1)
# Add line #
smgraphics.regressionplots.abline_plot(model_results=regression, ax=figure.axes[0])
Outliers: [(15, 220)]
Thanks for adding the new info! Great examples, they've really helped me understand it. –
Knitwear
Why do you consider values with
t < 0.5 as outliers? I think t is the Bonferroni-adjusted p-value. –
Beauty @Tupi what are x[i] and y[i] in the for loop of outliers? I mean what are they supposed to mean? As I can see
(i,t) is a tuple in enumerate(test). Also what is t[2]? –
Delladelle It's all specified in the documentation at statsmodels.org/dev/generated/… –
Tupi
scipy.stats doesn't have anything directly for outliers, so as answer some links and advertising for statsmodels (which is a statistics complement for scipy.stats)
for identifying outliers
http://jpktd.blogspot.ca/2012/01/influence-and-outlier-measures-in.html
http://jpktd.blogspot.ca/2012/01/anscombe-and-diagnostic-statistics.html
instead of masking, a better approach is to use a robust estimator
http://statsmodels.sourceforge.net/devel/rlm.html
with examples, where unfortunately the plots are currently not displayed http://statsmodels.sourceforge.net/devel/examples/generated/tut_ols_rlm.html
RLM downweights outliers. The estimation results have a weights attribute, and for outliers the weights are smaller than 1. This can also be used for finding outliers. RLM is also more robust if the are several outliers.
what is an exogenous design matrix? I have some x, y data: y = f(x). It's a mostly linear function: y = mx + b. Where do I start with this robust estimator? The terminology of the docs is impenetrable to me. –
Knitwear
More generally (i.e. programmatically) is there a way to identify and mask outliers?
Various outlier detection algorithms exist; scikit-learn implements a few of them.
[Disclaimer: I'm a scikit-learn contributor.]
Even though this question is very old now, I will still provide another answer based solely on numpy and scipy although the latter is rather optional.
Finding outliers in linear regressions is a quite common and yet tricky task. Fortunately, there are so-called measures of influence. Outliers have an unnaturally high influence on the regression and using by such measures they can be identified and rejected based on some rejection rules.
One common measure of influence is the Cook's distance D and another less common although more powerful one is the Peña sensitivity S, which are both described in the same Wikipedia article (disclaimer: I added the latter). From their basic idea, each data point is left out once and the change in the regression model is assessed. Data points whose removal changes the model a lot are most likely outliers (idea behind Cook's distance) and the same holds true for data points that are not really affected when other data points are removed (idea behind Peña sensitivity).
There is one big risk when many outliers are grouped together because then they can "mask" each other. If one removes one of these points, the model will not change because then all the other outliers keep it in position. That's why Cook's distance can fail and should thus be accompanied by Peña sensitivity.
That's about it for the theory behind. Please refer to the links if required. For the implementations, they can be carried out quite efficiently together with the regression itself and I want to demonstrate this using the example from
- Peña, D.: A New Statistic for Influence in Linear Regression, TECHNOMETRICS, FEBRUARY 2005, VOL. 47, NO. 1 (Table 1, p. 5)
As all the math is already described in the article, I will not go into detail here except for the general concept of the projection or "hat"-matrix H in linear regression. Basically the model y ~= X @ b (@ is the matrix or "dot" product) can also be phrased in terms of the projection matrix as y ~= H @ y. This will be used in the following code that computes the hat-matrix of a linear regression using Singular Value Decomposition. With this hat-matrix, the Cook's distance and Peña sensitivity are derived in one go. To make proper use of the SVD, which would otherwise need to be computed multiple times, we define 2 auxiliary functions for the regression. One to compute the coefficient vector b and another one to compute the rank of the matrix X, which is equal to the number of independent variables used in the regression (so this also work for correlated variables in X):
import numpy as np
# Definition of a regression function that uses a pre-computed Singular Value
# Decomposition (SVD) of the X-matrix
def lstsq_from_svd(
y_vect: np.ndarray,
u: np.ndarray,
s: np.ndarray,
vt: np.ndarray,
rcond: float | int = 1e-15,
) -> np.ndarray:
# all singular values that are numerically small are set to 0 after the inversion
large_s_idxs = np.where(s >= rcond * s.max())
inv_s = np.zeros_like(s)
inv_s[large_s_idxs] = 1.0 / s[large_s_idxs]
# now, the coefficient vector is computed as V @ inv(S) @ U.T @ y
return (vt.T * inv_s[np.newaxis, ::]) @ u.T @ y_vect
# Definition of a matrix rank function that uses a pre-computed SVD of the X-matrix
def matrix_rank_from_svd(
x_shape: tuple[int, int],
s: np.ndarray,
) -> int:
# first, the tolerance below which a singular value is considered 0 is evaluated
# (same behaviour as ``np.linalg.matrix_rank`` for ``tol=None``)
tol = s.max() * max(x_shape) * np.finfo(s.dtype).eps
return np.count_nonzero(s > tol)
The following implementation is kept general, so it can work with an arbitrary matrix X that is used for y ~= X @ b, so one can also use this to find outliers in a sinusoidal or a cubic polynomial fit. For assessing the importance of using both measures, 4 different scenarios with outliers that exhibit different levels of leverage on the regression are provided. The expression diag(R) extracts the main diagonal from a square matrix R. In contrast diag(r) turns the vector r into a diagonal matrix with r on its diagonal, just as np.diag does. Assertions are used to prove that all the simplifications made work and all equations and rejection rules involved are included as comments. Besides, the results were checked against the publication.
# Imports
from enum import StrEnum
from matplotlib import pyplot as plt
from scipy.stats import median_abs_deviation
# Specification of the global constants
POLYNOMIAL_DEGREE = 1
# Definition of 4 different outlier scenarios (based on their leverage)
class OutlierScenarios(StrEnum):
OUTLIER_FREE = "outlier free"
HIGH_LEVERAGE = "high leverage outliers" # 3 outliers
MEDIUM_LEVERAGE = "medium leverage outliers" # 3 outliers
LOW_LEVERAGE = "low leverage outliers" # 3 outliers
scenarios = [member for member in OutlierScenarios]
# "Reading" the base XY-data
xy_data = np.array(
[
[0.3899, 0.0],
[0.0880, -0.3179],
[-0.6355, 1.0950],
[-0.5596, -1.8740],
[0.4437, 0.4282],
[-0.9499, 0.8956],
[0.7812, 0.7310],
[0.5690, 0.5779],
[-0.8217, 0.0403],
[-0.2656, 0.6771],
[-1.1878, 0.5689],
[-2.2023, -0.2556],
[0.9863, -0.3775],
[-0.5186, -0.2959],
[0.3274, -1.4751],
[0.2341, -0.2340],
[0.0215, 0.1184],
[-1.0039, 0.3148],
[-0.9471, 1.4435],
[-0.3744, -0.3510],
[-1.1859, 0.6232],
[-1.0559, 0.7990],
[1.4725, 0.9409],
[0.0557, -0.9921],
[-1.2173, 0.2120],
[-0.412, 0.2379],
[-1.1283, -1.0078],
]
)
# definition of the outlier-containing datasets
outlier_datasets = {
OutlierScenarios.OUTLIER_FREE: np.array(
[
[1.02, 0.72],
[0.75, 0.42],
[-0.44, -0.21],
]
),
OutlierScenarios.HIGH_LEVERAGE: np.array([[20.0, 5.0]] * 3),
OutlierScenarios.MEDIUM_LEVERAGE: np.array([[5.0, 5.0]] * 3),
OutlierScenarios.LOW_LEVERAGE: np.array([[0.5, 5.0]] * 3),
}
# now, the ordinary regression is performed
fig_reg, ax_reg = plt.subplots(nrows=2, ncols=2, sharex="all", sharey="all")
plot_x_vect = np.linspace(start=-2.5, stop=20.5, num=101)
# running the main loop over all scenarios
for idx, scen in enumerate(scenarios):
# reading the outlier data ...
outlier_xy_data = outlier_datasets[scen]
# ... and concatenating them with the base-data
contam_x_vect = np.concatenate([xy_data[::, 0], outlier_xy_data[::, 0]])
contam_y_vect = np.concatenate([xy_data[::, 1], outlier_xy_data[::, 1]])
# now, the X-matrix for the system Xb ~= y is set up (N with + 1 since the constant
# also counts)
x_mat = np.vander(x=contam_x_vect, N=POLYNOMIAL_DEGREE + 1, increasing=True)
plot_x_mat = np.vander(x=plot_x_vect, N=POLYNOMIAL_DEGREE + 1, increasing=True)
# the coefficient vector is given by b = pinv(X) @ y where pinv(X) denotes the
# Moore-Penrose-Pseudoinverse which can be computed form the SVD, i.e.,
# X = U @ diag(s) @ V.T
u, s, vt = np.linalg.svd(a=x_mat, full_matrices=False)
coeff_b_vect = lstsq_from_svd(y_vect=contam_y_vect, u=u, s=s, vt=vt)
assert np.allclose(
np.linalg.lstsq(x_mat, contam_y_vect, rcond=None)[0], coeff_b_vect
), "SVD-based inversion incorrect"
# using the same SVD, the hat-matrix H = X @ pinv(X) can be computed. If pinv(X) is
# the left inverse of X, H is given by H = U @ U.T
hat_matrix = u @ u.T
assert np.allclose(
hat_matrix, x_mat @ np.linalg.pinv(x_mat)
), "Hat-matrix simplification incorrect"
# all that's missing is the residuals now given by r = y - X @ b ...
resid_vect = (contam_y_vect - x_mat @ coeff_b_vect)
# ... along with the mean squared error MSE = (r.T @ r) / (n - p) with
# n as the number of samples and p as the number of effective variables (=rank(X))
num_samples = x_mat.shape[0]
num_vars = matrix_rank_from_svd(x_shape=x_mat.shape, s=s)
mse = np.sum(resid_vect * resid_vect) / (x_mat.shape[0] - num_vars)
# using the equations given at
# https://en.wikipedia.org/wiki/Cook's_distance#Relationship_to_other_influence_measures_(and_interpretation)
# the Cooks's distance and Peña sensitivity can be computed
# as a basis, the T-matrix is produced as T = H @ diag(r) @ diag(1 / (1 - diag(H)))
# for all diagonal matrices involved, fast row-wise multiplication is used rather
# then ``@`` since most of the entries are 0s and the computational cost would thus
# be high for nothing
t_mat = hat_matrix * (resid_vect / (1.0 - np.diag(hat_matrix)))[np.newaxis, ::]
# the Cook's distances are defined as (1 / p / RMSE²) * diag(T.T @ T)
# since only the main diagonal is required, the columns of T * T can be summed
# individually instead
t_mat_squared = t_mat * t_mat
mse_prefact = 1.0 / (num_vars * mse)
cooks_d = mse_prefact * np.sum(t_mat_squared, axis=0)
assert np.allclose(
cooks_d, mse_prefact * np.diag(t_mat.T @ t_mat)
), "Cook simplification incorrect"
# the Peña sensitivities are defined as
# (1 / p / RMSE²) * diag(1 / diag(H)) @ diag(T @ T.T)
# here, the rows if T * T can be summed individually and for the diagonal product,
# element-wise division is a lot more efficient
pena_s = mse_prefact * (np.sum(t_mat_squared, axis=1) / np.diag(hat_matrix))
assert np.allclose(
pena_s,
mse_prefact * np.diag(1.0 / np.diag(hat_matrix)) @ np.diag(t_mat @ t_mat.T),
), "Peña simplification incorrect"
# according to the german Wikipedia, outliers can be flagged using (4 / n) as
# threshold for Cook's distance
cook_cutoff = 4.0 / x_mat.shape[0]
cook_outlier_mask = cooks_d > cook_cutoff
# for the Peña sensitivities, the rejection can be based on robust estimation of
# the normal distribution they follow and discarding datapoints that are far
# outide the tails
pena_median = np.median(pena_s)
pena_mad = median_abs_deviation(x=pena_s, scale=1.0)
pena_z_scores = (pena_s - pena_median) / pena_mad
pena_outlier_mask = np.abs(pena_z_scores) > 4.5
# Plotting all the results
ax_idxs = divmod(idx, 2)
ax_reg[ax_idxs].set_title(f"{scen}", fontsize=18)
ax_reg[ax_idxs].scatter(xy_data[::, 0], xy_data[::, 1], label="original datapoints")
ax_reg[ax_idxs].scatter(
outlier_xy_data[::, 0], outlier_xy_data[::, 1], c="red", label="added set"
)
ax_reg[ax_idxs].scatter(
contam_x_vect[cook_outlier_mask],
contam_y_vect[cook_outlier_mask],
s=150,
c="none",
ec="black",
lw=2.0,
label="flagged by Cook's D",
)
ax_reg[ax_idxs].scatter(
contam_x_vect[pena_outlier_mask],
contam_y_vect[pena_outlier_mask],
s=200,
marker="s",
c="none",
ec="black",
lw=2.0,
label="flagged by Peña's S",
)
ax_reg[ax_idxs].plot(
plot_x_vect, plot_x_mat @ coeff_b_vect, label="regression line", color="black"
)
if idx % 2 == 0:
ax_reg[ax_idxs].set_ylabel("y", fontsize=16)
if idx / 2 >= 1:
ax_reg[ax_idxs].set_xlabel("x", fontsize=16)
if idx == 0:
legend = ax_reg[ax_idxs].legend(ncol=2, loc="best", fontsize=14)
plt.show()
This example yields the following plot:
Comparison of outliers flagged by Cook's distance and Peña sensitivity
So, neither of them is superior in every scenario, and they should both be used combined.
A few remarks:
- changing
POLYNOMIAL_DEGREEto2will show how outliers are flagged for a parabola fit and - fun fact - changing it to0will be finding outliers in computation of the mean of the y-data because that's nothing but a linear regression problem with solely the constant. In this case, the Peña sensitivity becomes ill-conditioned though. - weighted regression can also be used, but then H = U @ U.T will no longer hold because then H = X @ pinv(sqrt(W) @ X) @ sqrt(W) where W is the inverted variance-covariance matrix of the errors in y. Also the coefficients are then b = pinv(sqrt(W) @ X) @ sqrt(W) @ y. The residuals and the MSE then also require weighting r_w = sqrt(W) @ (y - X @ b) and wMSE = (r.T @ W @ r) / (n - p)
- the use of 4.5 median absolute deviations (MAD) for the Peña sensitivity rejection rule means that all S-values that are 3 robust standard deviations from the median are rejected as outliers because ~1.5 times the MAD resembles the standard deviation for normally distributed data. Bascially, any other robust measure of scale can be used to robustly estimate the standard deviation, such as the Qn-scale or the biweight midvariance that behave more favourably for normal distributions.
- the concept can be extended to any other linear projection y ~= H @ y, such as smoothing. Let's take the well known Savitzky-Golay-filter. Except for the boundaries - that require special treatment in case one wants to make it really accurate - its hat-matrix H is a Toeplitz-matrix that can be computed by the code below. It's easy to see that each of its rows is the kernel shifted by one such as the filtering method is intended:
from scipy.linalg import convolution_matrix
from scipy.signal import savgol_coeffs
# setup of a Savitzky-Golay-filter with 3rd order polynomial and window-length 5 for
# a signal of arbitrary length n
POLYDEGREE = 3
WINDOW_LENGTH = 5
savgol_kernel = savgol_coeffs(
window_length=WINDOW_LENGTH, polyorder=POLYDEGREE, deriv=0
)
print(savgol_kernel)
# [-0.08571429 0.34285714 0.48571429 0.34285714 -0.08571429]
hat_matrix = convolution_matrix(a=savgol_kernel, n=6, mode="same")
print(hat_matrix)
# [[ 0.48571429 0.34285714 -0.08571429 0. 0. 0. ]
# [ 0.34285714 0.48571429 0.34285714 -0.08571429 0. 0. ]
# [-0.08571429 0.34285714 0.48571429 0.34285714 -0.08571429 0. ] # one full kernel
# [ 0. -0.08571429 0.34285714 0.48571429 0.34285714 -0.08571429] # one full kernel
# [ 0. 0. -0.08571429 0.34285714 0.48571429 0.34285714]
# [ 0. 0. 0. -0.08571429 0.34285714 0.48571429]]
then, also the number of variables needs to be calculated in a more involved way using the trace of the hat-matrix and its product with itself.
In case one wants to go really elaborate, an eigenvalue analysis on the matrices that lead to the Cook's distance and the Peña sensitivity can be carried out (as mentioned in the Wikipedia article).
Hope this helps!
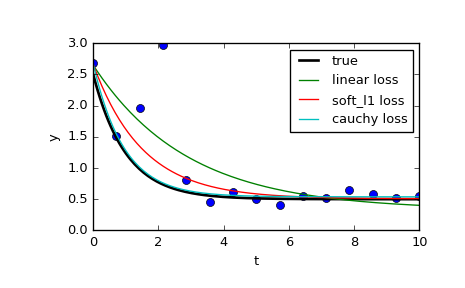
It is also possible to limit the effect of outliers using scipy.optimize.least_squares. Especially, take a look at the f_scale parameter:
Value of soft margin between inlier and outlier residuals, default is 1.0. ... This parameter has no effect with loss='linear', but for other loss values it is of crucial importance.
On the page they compare 3 different functions: the normal least_squares, and two methods involving f_scale:
res_lsq = least_squares(fun, x0, args=(t_train, y_train))
res_soft_l1 = least_squares(fun, x0, loss='soft_l1', f_scale=0.1, args=(t_train, y_train))
res_log = least_squares(fun, x0, loss='cauchy', f_scale=0.1, args=(t_train, y_train))
As can be seen, the normal least squares is a lot more affected by data outliers, and it can be worth playing around with different loss functions in combination with different f_scales. The possible loss functions are (taken from the documentation):
‘linear’ : Gives a standard least-squares problem.
‘soft_l1’: The smooth approximation of l1 (absolute value) loss. Usually a good choice for robust least squares.
‘huber’ : Works similarly to ‘soft_l1’.
‘cauchy’ : Severely weakens outliers influence, but may cause difficulties in optimization process.
‘arctan’ : Limits a maximum loss on a single residual, has properties similar to ‘cauchy’.
The scipy cookbook has a neat tutorial on robust nonlinear regression.
© 2022 - 2024 — McMap. All rights reserved.