Many skipped stages for Pregel in Spark UI

Question

I try to run connected components on logNormalGraph.

val graph: Graph[Long, Int] = GraphGenerators.
    logNormalGraph(context.spark, numEParts = 10, numVertices = 1000000,
        mu = 0.01, sigma = 0.01)

val minGraph = graph.connectedComponents()

And in the spark UI for every next job I can see constantly growing number of skipped stages

1 - 4/4 (12 skipped)
2 - 4/4 (23 skipped)
...
50 - 4/4 (4079 skipped)

Why there are so many skipped stages when I run something on Pregel and why this number is growing so fast (non-linearly)?

Incertitude

Answer 1

Step by step. connectedComponents function is implemented using Pregel API. Ignoring algorithm specific details it iteratively:

• joinVertices caching the output
• mapReduceTriplets over messages

First lets create dummy sendMsg:

import org.apache.spark.graphx._

def sendMsg(edge: EdgeTriplet[VertexId, Int]): 
    Iterator[(VertexId, VertexId)] = {
  Iterator((edge.dstId, edge.srcAttr))
}

vprog:

val vprog =  (id: Long, attr: Long, msg: Long) => math.min(attr, msg)

and megeMsg:

val mergeMsg = (a: Long, b: Long) => math.min(a, b)

Next we can initialize example graph:

import org.apache.spark.graphx.util.GraphGenerators

val graph = GraphGenerators.logNormalGraph(
   sc, numEParts = 10, numVertices = 100,  mu = 0.01, sigma = 0.01)
  .mapVertices { case (vid, _) => vid }

val g0 = graph
  .mapVertices((vid, vdata) => vprog(vid, vdata, Long.MaxValue))
  .cache()

and messages:

val messages0 = g0.mapReduceTriplets(sendMsg, mergeMsg).cache()

Since GraphXUtils are private we have to use Graph methods directly.

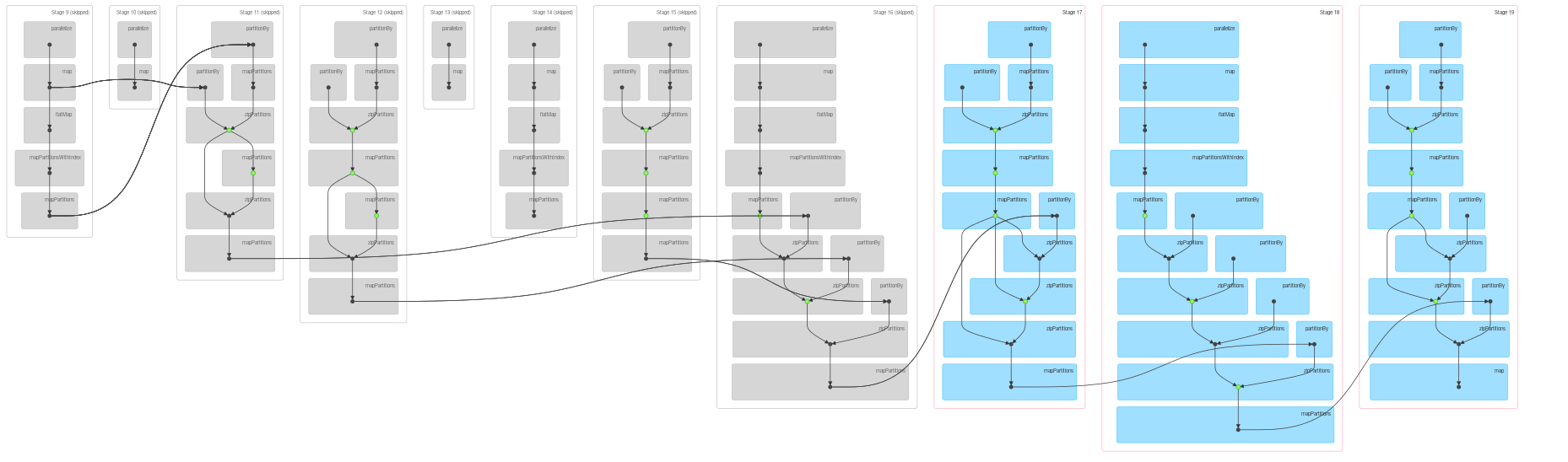
When you take a look at the DAG generated by

messages0.count

you'll already see some skipped stages:

After executing the first iteration

val g1 = g0.joinVertices(messages0)(vprog).cache()
val messages1 = g1.mapReduceTriplets(sendMsg, mergeMsg).cache()
messages1.count

graph will look more or less like this:

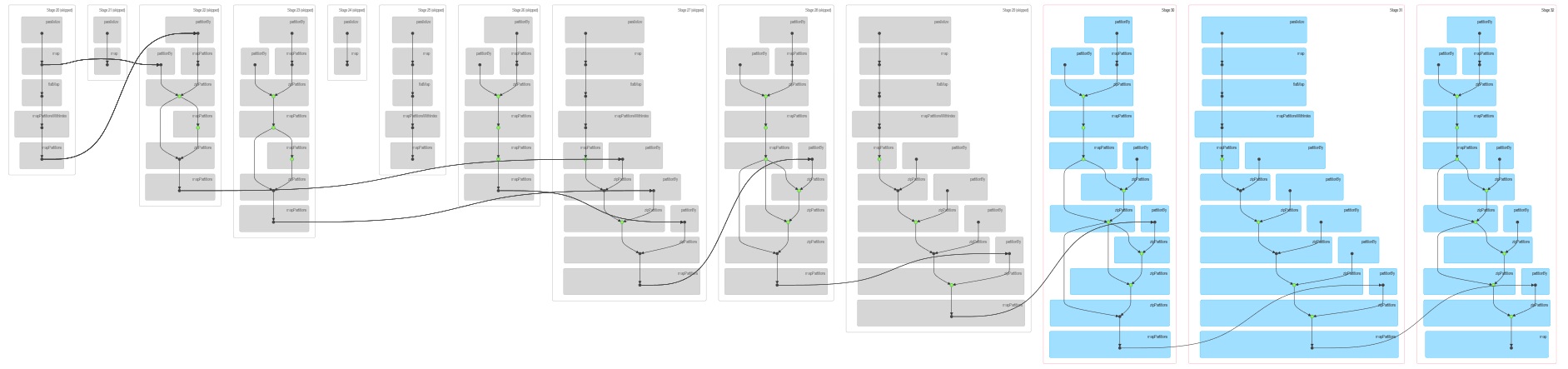
If we continue:

val g2 = g1.joinVertices(messages1)(vprog).cache()
val messages2 = g2.mapReduceTriplets(sendMsg, mergeMsg).cache()
messages2.count

we get following DAG:

So what happened here:

• we execute iterative algorithm which takes a dependency on the same data twice, once for join and once for message aggregation. This leads to increasing number of stages on which g depends in each iteration
• since data is intensively cached (explicitly as you can see in the code, explicitly by persisting shuffle files) and checkpointed (I could be wrong here, but checkpoints are typically marked as green dots) each stage has to be computed only once, even if multiple downstream stages depend on it.
• after data is initialized (g0, messages0) only the the latest stages are computed from scratch.
• if you take a closer look at DAG you'll see that there are quite complex dependencies which should account for remaining discrepancies between relatively slow growth of DAG and number of skipped stages.

The first property explains growing number of stages, the second one the fact that stages are skipped.

Benito