How to set 0 to white at an uneven colormap

Question

I have an uneven colormap and I want the 0 to be white. All negative colors have to be bluish and all positive colors have to be reddish. My current attempt displays the 0 bluish and the 0.7 white.

Is there any way to set the 0 to white?

import numpy as np
import matplotlib.colors as colors 
from matplotlib import pyplot as m

bounds_min = np.arange(-2, 0, 0.1)
bounds_max = np.arange(0, 4.1, 0.1)
bounds = np.concatenate((bounds_min, bounds_max), axis=None)       
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)      # I found this on the internet and thought this would solve my problem. But it doesn't...
m.pcolormesh(xx, yy, interpolated_grid_values, norm=norm, cmap='RdBu_r')

Baguio

Answer 1

The other answer makes it a little more complicated than it needs to be. In order to have the middle point of the colormap at 0, use a DivergingNorm with vcenter=0.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import DivergingNorm

x, y = np.meshgrid(np.linspace(0,50,51), np.linspace(0,50,51))
z = np.linspace(-2,4,50*50).reshape(50,50)

norm = DivergingNorm(vmin=z.min(), vcenter=0, vmax=z.max())
pc = plt.pcolormesh(x,y,z, norm=norm, cmap="RdBu_r")
plt.colorbar(pc)

plt.show()

Note: From matplotlib 3.2 onwards DivergingNorm will be renamed to TwoSlopeNorm

Etz

Similar to here question I wanted to produce a figure with all blue pixels showing intensity if negative values and red ones for the positive. It is important to notice, if you don't want any green in your final rgb figure, you should produce your own colormap by importing: from matplotlib.colors import LinearSegmentedColormap <=== and then creating something like: cmap=LinearSegmentedColormap.from_list('rg',["r", "b"], N=256). <=== The same goes for red and green colormap. – Phelps

Answer 2

In order to get the desired norm, set the same number of colors on the negative as on the positive side.

Alternatively, you could use the unmodified norm, and create a special colormap. Such a colormap would have 1/3^rd of blue-to-white colors and 2/3^rd white-to-red colors. A benefit would be that the colorbar looks nicer. Such an approach only works if the balance between negative and positive numbers isn't too extreme.

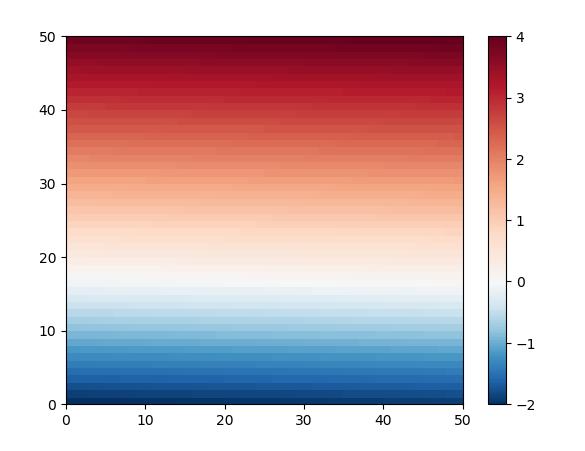
Here is demo code with generated data. zz is chosen to be a sine rotated around the center, and scaled to go from -2 to 4, so symmetric around 1. At the left the image is shown with the modified colormap. At the right, the norm is changed to force white at zero.

Because of the red coloring of all positive values, the red bands are wider than the blue. In an image without changing norms nor colormaps, the bands would have equal width. The colorbars indicate the zero to be white.

import numpy as np
import matplotlib.colors as colors
from matplotlib import pyplot as plt

x = np.linspace(-20, 20, 500)
y = np.linspace(-20, 20, 500)
xx, yy = np.meshgrid(x, y)
zz = np.sin(np.sqrt(xx * xx + yy * yy)) * 3 + 1

negatives = -2.0
positives = 4.0

bounds_min = np.linspace(negatives, 0, 129)
bounds_max = np.linspace(0, positives, 129)[1:]
    # the zero is only needed once
    # in total there will be 257 bounds, so 256 bins
bounds = np.concatenate((bounds_min, bounds_max), axis=None)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)

num_neg_colors = int(256 / (positives - negatives) * (-negatives))
num_pos_colors = 256 - num_neg_colors
cmap_BuRd = plt.cm.RdBu_r
colors_2neg_4pos = [cmap_BuRd(0.5*c/num_neg_colors) for c in range(num_neg_colors)] +\
                   [cmap_BuRd(1-0.5*c/num_pos_colors) for c in range(num_pos_colors)][::-1]
cmap_2neg_4pos = colors.LinearSegmentedColormap.from_list('cmap_2neg_4pos', colors_2neg_4pos, N=256)

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))

mesh1 = ax1.pcolormesh(xx, yy, zz, cmap=cmap_2neg_4pos)
ax1.set_aspect('equal')
ax1.set_title('using a modified cmap')
fig.colorbar(mesh1, ax=ax1)

mesh2 = ax2.pcolormesh(xx, yy, zz, norm=norm, cmap='RdBu_r')
ax2.set_aspect('equal')
ax2.set_title('using a special norm')
ticks = np.append(np.arange(-2.0, 0, 0.25), np.arange(0, 4.001, 0.5))
fig.colorbar(mesh2, ax=ax2, ticks=ticks)

plt.show()

Following code plots the norm, which looks like a step function. Only with 257 bounds this step function has the correct shape everywhere (zooming to x at -2, 0 and 4).

nx = np.linspace(-3,5,10000)
plt.plot(nx, norm(nx))

PS: There is an alternative method to create a similar colormap. But trying it out, it is clear that the RdBu colormap is fine-tuned and produces much better looking plots.

norm_2neg_4pos = mcolors.Normalize(negatives, positives)
colors_2neg_4pos = [[0, 'blue'],
                    [norm_2neg_4pos(0.0), "white"],
                    [1, 'red']]
cmap_2neg_4pos = mcolors.LinearSegmentedColormap.from_list("", colors_2neg_4pos)

Still another simple solution is rescaling everything between -4 and 4. However, this would lose the darker blues. An alternative to 'RdBu_r' is 'seismic' with a different way to run from red over white to blue.

ax.pcolormesh(xx, yy, zz, vmin=-positives, vmax=positives, cmap='RdBu_r')

Ascham

Thank you for your help! It took me a while to get it right, but now it works. Do you know if it is possible to have the negative bar shorter than the positive bar? – Baguio

Yes, that can also be done. In that case, the norm is not needed, only the colormap needs to be recalculated. It won't work well if there is a huge difference between negative and positive, but with a factor of 2 it would work well. Give me some time to create an example. – Ascham