When to use noEvent operator in Modelica language?

Question

The noEvent operator in Modelica doesn't use iteration to find the precise time instant in which the event was triggered.

It seems this would cause calculation error, here is an example I find on the following website https://mbe.modelica.university/behavior/discrete/decay/ So Do I have to ensure the function is smooth when using noEvent operator? What's the purpose of using noEvent operator if it can't ensure accuracy?

Traveled

Can you add a reference/link for the first screenshot you have added? The part before the "Additionally, the noEvent() ..." seems a bit strange to me. I would like to get some more context... – Milesmilesian

It is from the page 238 of a free e-book, you could download it from e-uned.es/product/product.php?prdctID=759, it is a textbook for MOOC(iedra.uned.es/courses/course-v1:UNED+Modelsimul_02+2020_T1/…) – Traveled

I think if I could find the detailed process of how noEvent operator finding the right point to change from one branch to another, it would be more clear to solve the question. Could anyone tell me where to find the related information? – Traveled

There would be no error with the following setting. imgur.com/RAcRaCp – Traveled

I think reading mbe.modelica.university/behavior/discrete/events including the link to "Event supression" should give a good idea on when to use noEvent and possibly smooth(). – Milesmilesian

Answer 1

Based on the two different ways of dealing with the event. If using noEvent operator, there is no halt of the integration, but the numerical solver assumes that the function should be smooth, with unsmooth functions, there would be numerical errors.

Traveled

Do you have a source for the screenshot? – Milesmilesian

I can't remember exactly where to find this picture, I will try to figure it out. – Traveled

Answer 2

Although the question is already answered I would like to add some points, as I think it could be useful for many.

There are some common reasons to use the noEvent() statement:

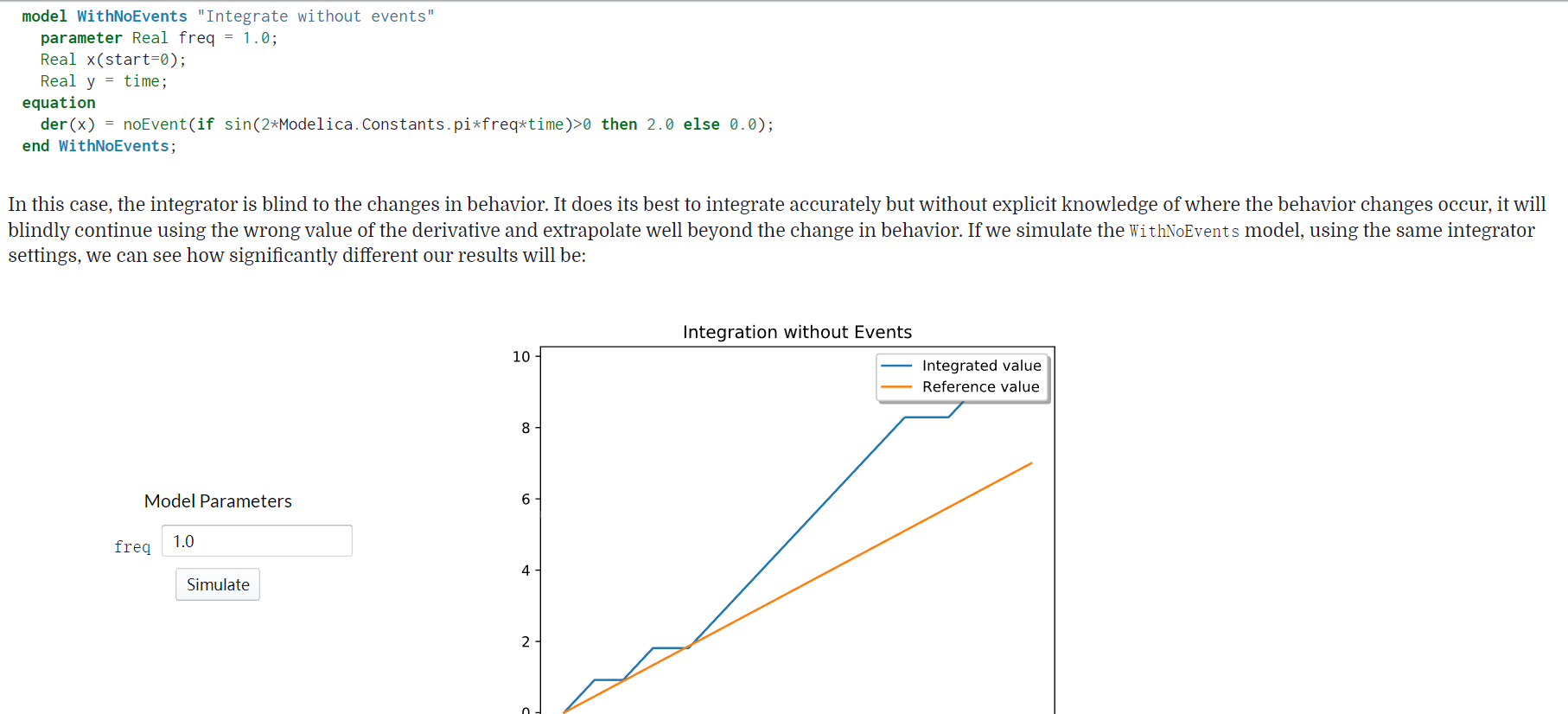
1. Guarding expressions: This is used to prevent a function from being evaluated outside of their validity range. A typical example is der(x) = if x>=0 then sqrt(x) else 0; which would work perfectly in most common programming languages. This doesn't work always in Modelica for the following reason: When searching for the time when the condition x>=0 becomes false, it is possible that both branches are evaluated with values of x varying around 0. The same fact is mentioned in the screenshot posted by marvel This results in a crash if the square root of a negative x is evaluated. Therefore der(x) = if noEvent(x>=0) then -sqrt(x) else 0; Is used to suppress the iteration to search for the crossing time, leaving the handling of the discontinuity to the solver (often referred to as "expressions are taken literally instead of generating crossing functions"). In case of a variable step-size solver being used, this makes the solver reduce the step-size to meet it's relative error tolerance, which will likely result in degraded performance. Additionally this can be critical if the function described is not smooth enough resulting in non-precise or even instable simulations.

2. Continuous Expressions: When a function is continuous there is actually no event necessary. This comes down to the fact, that events are used to describe discontinuities. So if there is none, usually the event is simply superfluous and can therefore be suppressed. This is actually covered by the smooth() operator in Modelica, but the specification says, that a tool is free to still generate events. To my experience, tools generate events if the change to the function is relatively big. Therefore it can make sense to have a noEvent() within a smooth().

3. Avoid chattering: noEvent can help here but actually chattering is a more general problem. Therefore I'd recommend to solve issues related to chattering by re-building the model.

If none of the above is true the use of noEvent should be considered carefully.

Milesmilesian

Answer 3

I think the Modelica Language Specification Version 3.4 Section 3.7.3.2. and Section 8.5. will help you out here (in case you have not already checked this).

From what i know it should only be used for efficiency reasons and in most cases one should use smooth() instead or in conjunction.

Notch

I already read the two sections, but I got confused about the so-called way of dealing with the math literally with noEvent, I mean whether noEvent require the math function is smooth enough so that there won't errors like in my question above. – Traveled

I would say that noEvent should only be used when needed, e.g, if noEvent(d>0 then d^0.5 else -(-d)^0.5; would without noEvent evaluate the wrong branch when d switches sign which will fail; and not for efficiency reasons. Technically it doesn't have to be smooth - so you could write if noEvent(d>0) then d^0.5 else 2; but I don't recommend it. – Rhinoplasty

My main confusion is that if noEvent doesn't precisely calculate the right time in which the event is triggered, how would the integrator ensure the accuracy in the following code if noEvent(d>0 then d^0.5 else -(-d)^0.5)? – Traveled

It does not and that is the point. Using noEvent() implies that this can be handled in a sloppy fashion and that it will have no great effect if the event happens at a slightly wrong time. Hans is right though about his usage example, i did not think of that case (the brackets are wrong it needs to be if noEvent(d>0) then d^0.5 else -(-d)^0.5). In that particular case it does not matter since the discontinuity still is smooth in it's result and in that case one could use something like sign(d)*abs(d)^0.5, but that is not always easy to find or does not even exist. – Notch