Generate graph from a list of connected components

Question

Setup

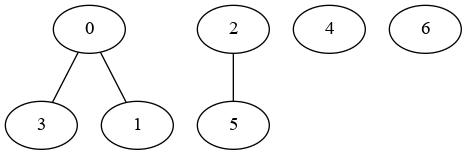
Let's assume the following undirected graph:

import networkx as nx

G = nx.from_edgelist([(0, 3), (0, 1), (2, 5), (0, 3)])
G.add_nodes_from(range(7))

or even adding the (1, 3) edge (it doesn't matter here):

The connected components are:

list(nx.connected_components(G))
# [{0, 1, 3}, {2, 5}, {4}, {6}]

Question

Is it possible to generate the graph G from the list of connected components directly with networkx? Or using a simple method?

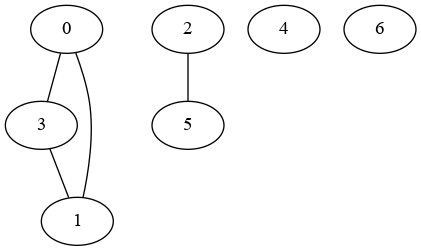
The only solution I found so far is to generate the successive edges or all combinations of nodes per group and feed it to nx.from_edgelist, then to add the single nodes with add_nodes_from:

from itertools import pairwise, chain

l = [{0, 1, 3}, {2, 5}, {4}, {6}]

G = nx.from_edgelist(chain.from_iterable(pairwise(e) for e in l))
G.add_nodes_from(set.union(*l))

or for all edges:

from itertools import combinations, chain

l = [{0, 1, 3}, {2, 5}, {4}, {6}]

G = nx.from_edgelist(chain.from_iterable(combinations(e, 2) for e in l))
G.add_nodes_from(set.union(*l))

Baxter

The question is which edges you want to assume between the nodes in the connected components. Simple choices would be either fully connected (as you did) or a simple line. As long as each node has at least one edge - or in other words as long as the connected component consists of at least 2 nodes - you don't need to additionally add the nodes via add_nodes_from. – Barela

@Barela the exact edges do not really matter here (ideally a solution for both: "first from list order" and "all connected" would be nice). Regarding adding the existing nodes, I know it's not required I just added all for simplicity ;) – Baxter

Don't use permutations. Use combinations. There are exactly twice as many elements in permutations(cc, 2) as in combinations(cc, 2), and those are all redundant elements if G is a simple undirected graph. – Calzada

"of course combinations would give the first graph and permutations the second one." I don't understand. Why would combinations and permutations give different graphs? My point is precisely that they would give the exact same graph, but combinations is more efficient. – Calzada

@Baxter I just ran the two code snippets from your update. The two graphs have the exact same list of edges. – Calzada

Also note that G = nx.from_edgelist(chain.from_iterable(list(combinations(e, 2)) for e in l)) is equivalent to G = nx.from_edgelist(chain(combinations(cc, 2) for cc in l)). You don't need to build a list( ) then use .from_iterable. – Calzada

@Calzada I simplified the question to focus on my real question. This was just an example here. What I really care about is to know if networkx can do this natively. (NB. you were right on the edgelist btw, I hadn't checked) – Baxter

Also note that if you don't care about collecting all edges, just about collecting enough edges to get the same connected components, then you only need one path per connected component. This can be obtained with pairwise: from itertools import pairwise; G = nx.from_edgelist(pairwise(cc) for cc in l). Then you have a number of edges which is linear instead of quadratic. – Calzada

Yes this is what I meant (pairwise/combination not combinations/permutations), but again, not the question ;) – Baxter

@Calzada I updated the question, thanks for your correction (I had brainfreeze when writing it), Now I hope to get a networkx answer – Baxter

Okay, how about G = nx.union_all(nx.path_graph(cc) for cc in l) (equivalent to using pairwise) or G = nx.union_all(nx.complete_graph(cc) for cc in l) (equivalent to using combinations) – Calzada

@Calzada that's quite nice! (especially using map). Thanks! (don't hesitate if you want to post as answer). Would you know an equivalent for all combinations of edges? – Baxter

Answer 1

An alternative to itertools.pairwise is networkx.path_graph.

An alternative to itertools.combinations is networkx.complete_graph.

These two networkx functions return a new graph, not a list of edges, so you can combine them with networkx.compose_all.

Note also union_all and disjoint_union_all as alternatives to compose_all.

import networkx as nx

l = [{0, 1, 3}, {2, 5}, {4}, {6}]

G = nx.compose_all(map(nx.path_graph, l))

H = nx.compose_all(map(nx.complete_graph, l))

print(G.nodes, G.edges)
# [0, 1, 3, 2, 5, 4, 6] [(0, 1), (1, 3), (2, 5)]

print(H.nodes, H.edges)
# [0, 1, 3, 2, 5, 4, 6] [(0, 1), (0, 3), (1, 3), (2, 5)]

I haven't actually run benchmarks, but I suspect creating several graphs and composing them might be slower than creating lists of edges and chaining them to create only one graph.

Calzada

Small feedback. The itertools version seem much faster (~10-20x), which is probably expected. I also realized it would fail on such input l = [{0, 1, 3}, {2, 5}, {4}, {6, 0}] (which is not strictly a list of connected components), but I found that compose_all would work well in this case. Very nice tools, I'm learning to love it ;) – Baxter