solving XOR with single layer perceptron

Question

I've always heard that the XOR problem can not be solved by a single layer perceptron (not using a hidden layer) since it is not linearly separable. I understand that there is no linear function that can separate the classes.

However, what if we use a non-monotonic activation function like sin() or cos() is this still the case? I would imagine these types of functions might be able to separate them.

Bib

Answer 1

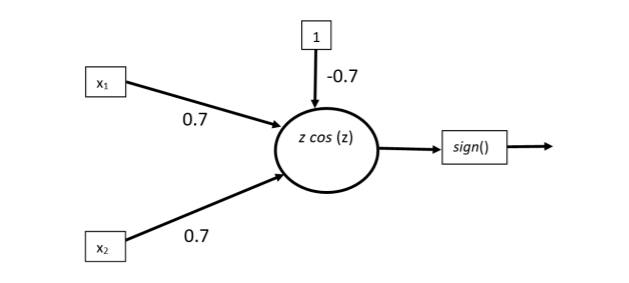
Yes, a single layer neural network with a non-monotonic activation function can solve the XOR problem. More specifically, a periodic function would cut the XY plane more than once. Even an Abs or Gaussian activation function will cut it twice.

Try it yourself: W1 = W2 = 100, Wb = -100, activation = exp(-(Wx)^2)

• exp(-(100 * 0 + 100 * 0 - 100 * 1)^2) = ~0
• exp(-(100 * 0 + 100 * 1 - 100 * 1)^2) = 1
• exp(-(100 * 1 + 100 * 0 - 100 * 1)^2) = 1
• exp(-(100 * 1 + 100 * 1 - 100 * 1)^2) = ~0

Or with the abs activation: W1 = -1, W2 = 1, Wb = 0 (yes, you can solve it even without a bias)

• abs(-1 * 0 + 1 * 0) = 0
• abs(-1 * 0 + 1 * 1) = 1
• abs(-1 * 1 + 1 * 0) = 1
• abs(-1 * 1 + 1 * 1) = 0

Or with sine: W1 = W2 = -PI/2, Wb = -PI

• sin(-PI/2 * 0 - PI/2 * 0 - PI * 1) = 0
• sin(-PI/2 * 0 - PI/2 * 1 - PI * 1) = 1
• sin(-PI/2 * 1 - PI/2 * 0 - PI * 1) = 1
• sin(-PI/2 * 1 - PI/2 * 1 - PI * 1) = 0

Bayern

Answer 2

No, not without "hacks"

The reason why we need a hidden layer is intuitively apparent when illustrating the xor problem graphically.

You cannot draw a single sine or cosine function to separate the two colors. You need an additional line (hidden layer) as depicted in the following figure:

Literality

But lets suppose a non monotonic function exists that locally looks like this: i.imgur.com/Qi1FM3n.png This would surely separate the classes right? Could we not rotate / transform the sin/cos functions to get the same behaviour? – Bib

A function cannot map to two different x values. If the graph maps eg: x=0 -> y = 0.8 and y = -0.8 (as in the image you posted), it cannot be described by a regular function. This prevents us from using any methods requiring a derivate of the activation function. – Literality

I don't quite understand why this is the case in a (single layer) perceptron. We can simply update the weights using the difference between the desired output and and output calculated right? – Bib

I think that the transforming into a new feature space after linear transformation(which obviously should have well-selected coefficients) can change position of data in 2D-space. And that can be divided by non-monotonic function. – Bract

Answer 3

In a recent paper, the authors designed a neuron they called Growing Cosine Unit(GCU):

Hildebrand