NetworkX: adjacency matrix does not correspond to graph

Question

Say I have two options for generating the Adjacency Matrix of a network: nx.adjacency_matrix() and my own code. I wanted to test the correctness of my code and came up with some strange inequalities.

Example: a 3x3 lattice network.

import networkx as nx
N=3
G=nx.grid_2d_graph(N,N)
pos = dict( (n, n) for n in G.nodes() )
labels = dict( ((i,j), i + (N-1-j) * N ) for i, j in G.nodes() )
nx.relabel_nodes(G,labels,False)
inds=labels.keys()
vals=labels.values()
inds.sort()
vals.sort()
pos2=dict(zip(vals,inds))
plt.figure()
nx.draw_networkx(G, pos=pos2, with_labels=True, node_size = 200)

This is the visualization:

The adjacency matrix with nx.adjacency_matrix():

B=nx.adjacency_matrix(G)
B1=B.todense()

[[0 0 0 0 0 1 0 0 1]
 [0 0 0 1 0 1 0 0 0]
 [0 0 0 1 0 1 0 1 1]
 [0 1 1 0 0 0 1 0 0]
 [0 0 0 0 0 0 0 1 1]
 [1 1 1 0 0 0 0 0 0]
 [0 0 0 1 0 0 0 1 0]
 [0 0 1 0 1 0 1 0 0]
 [1 0 1 0 1 0 0 0 0]]

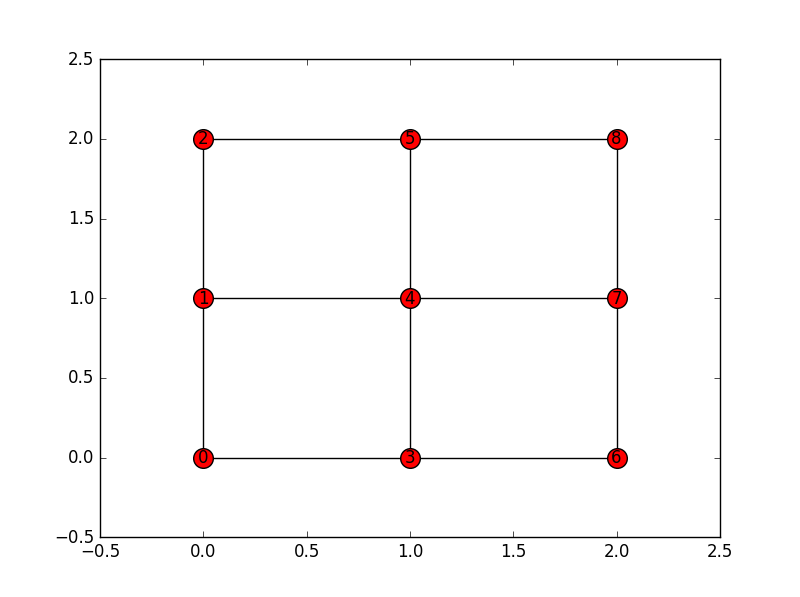
According to it, node 0 (entire 1st row and entire 1st column) is connected to nodes 5 and 8. But if you look at the image above this is wrong, as it connects to nodes 1 and 3.

Now my code (to be run in in the same script as the above):

import numpy
import math

P=3

def nodes_connected(i, j):
     try: 
        if i in G.neighbors(j):
            return 1
     except nx.NetworkXError:
        return False          

A=numpy.zeros((P*P,P*P))

for i in range(0,P*P,1):
    for j in range(0,P*P,1):

        if i not in G.nodes():
            A[i][:]=0
            A[:][i]=0
        elif i in G.nodes():
            A[i][j]=nodes_connected(i,j)
                A[j][i]=A[i][j]

for i in range(0,P*P,1):
    for j in range(0,P*P,1):
            if math.isnan(A[i][j]):
                A[i][j]=0 

print(A)

This yields:

[[ 0.  1.  0.  1.  0.  0.  0.  0.  0.]
 [ 1.  0.  1.  0.  1.  0.  0.  0.  0.]
 [ 0.  1.  0.  0.  0.  1.  0.  0.  0.]
 [ 1.  0.  0.  0.  1.  0.  1.  0.  0.]
 [ 0.  1.  0.  1.  0.  1.  0.  1.  0.]
 [ 0.  0.  1.  0.  1.  0.  0.  0.  1.]
 [ 0.  0.  0.  1.  0.  0.  0.  1.  0.]
 [ 0.  0.  0.  0.  1.  0.  1.  0.  1.]
 [ 0.  0.  0.  0.  0.  1.  0.  1.  0.]]

which says that node 0 is connected to nodes 1 and 3. Why does such difference exist? What is wrong in this situation?

Marika

not 100% sure, but related to the answer below, where you use dict above, you should change to using collections.OrderedDict... – Pie

Answer 1

Networkx doesn't know what order you want the nodes to be in.

Here is how to call it: adjacency_matrix(G, nodelist=None, weight='weight').

If you want a specific order, set nodelist to be a list in that order. So for example adjacency_matrix(G, nodelist=range(9)) should get what you want.

Why is this? Well, because a graph can have just about anything as its nodes (anything hashable). One of your nodes could have been "parrot" or (1,2). So it stores the nodes as keys in a dict, rather than assuming it's the non-negative integers starting at 0. Dict keys have an arbitrary order.

Cronin

Answer 2

A more general solution, if your nodes have some logical ordering as is the case if you generate a graph using G=nx.grid_2d_graph(3,3) (which returns tupples from (0,0) to (2,2), or in your example would be to use:

adjacency_matrix(G,nodelist=sorted(G.nodes()))

This sorts the returned list of nodes of G and passes it as the nodelist

Swinton