Algorithm to calculate the shortest path between two points on the surface of a 3D mesh

Question

I am looking for an algorithm to calculate the following:

I have:

1. A 3D triangle mesh. The triangles do not necessarily lie in one plane. The angle between the norm vectors of two neighbouring triangles is less then 90 degrees.

2. Two points. The two points lie either on an edge of the triangle mesh or inside a triangle of the mesh.

I need to calculate the polyline which represents the shortest path between the two points on the mesh.

What is the simplest and/or most effective strategy to do this?

Noose

Search for 'geodesic path'. Similar question – Amor

Answer 1

As it stands, your problem is not well defined; there can be many solutions depending on the direction used to "project" the line segment onto the mesh.

Once you have chosen the direction of projection, flatten the mesh onto a plane perpendicular to the direction of projection. At this point, your mesh is a collection of 2d edges (line segments); just determine the intersection (if any) of each edge with your target line segment.

---

Edit:

The updated question is now well defined. Since my answer to the original question (above) has been marked as accepted, presumably that means the information given in the comments below are actually what was really being "accepted" for the update question. I'll summarize:

• A google search of "shortest distance on 3d mesh" turns up some relevant information, like Shortest Path Approximation on Triangulated Meshes
• Also, see: https://mcmap.net/q/646030/-shortest-paths-amp-geodesics -- danh

Uremia

I am not sure if I understand this correctly. I could use for each triangle the triangle's norm vector as direction of the projection. Would that make sense? – Noose

You are going to have to clarify the problem: what is this projected line segment? What is this physical problem you are trying to solve? Because in my interpretation of it, using the mesh face's normals for the line segment projection does not make sense. – Uremia

Actually I am looking for the shortest connection between the two end points of the given line segment. – Noose

Sounds like your title should read something like "Algorithm to calculate the shortest path on the surface of a 3D mesh, between 2 points". If so, please update the question. – Uremia

A quick google search of "shortest distance on 3d mesh" turns up some relevant information, like Shortest Path Approximation on Triangulated Meshes – Uremia

Thank you for all your answers. I changed the question. – Noose

What's not well defined about "shortest distance between two points on a mesh"? Not well defined is different than very difficult. See here: https://mcmap.net/q/646030/-shortest-paths-amp-geodesics – Pictish

@Pictish The question text (including title) has changed from the original question. The new question description is well defined, and interesting. – Uremia

@Uremia - I see. You're right. Sorry I didn't check that before commenting. – Pictish

Answer 2

A standard approach to this task of finding the shortest path polyline (or geodesic) on the surface of triangular mesh between two given points consists of two steps:

1. Find a path approximation between two points
2. Iteratively adjust it to make it locally shortest everywhere.

The first step (path approximation) can be computed, for example, using

• Dijkstra algorithm, which considers only paths along mesh edges (no crossing of mesh triangles),
• Or some variations of Dijkstra algorithm, better suited for near planar surfaces like A*-search,
• Or it can be Fast marching method, which can find also the paths crossing the triangles, however not guaranteed to produce a geodesic line.

The next step is iterative adjustment of the approximate path till it becomes truly locally shortest. Some recent articles are really promising here, like Just Flipping Edges. But it requires to construct a path network from the original mesh before operating, so it can be really expensive if your task is just to find one shortest path on the mesh.

A more classical way is to consider every piece of current path approximation between it enters two consecutive vertices, and unfold the strip of crossed triangles on plane. Then find the shortest path in the planar strip, which is a task that can be solved exactly in a linear time, for example by Shortest Paths in Polygons method by Wolfgang Mulzer. The crossing of this line with the edges will give the shortest path on the mesh in between two vertices.

Then for every vertex on the path approximation, two walks around this vertex are evaluated using same unfolding in hope a path around will be shorter then the path exactly via the vertex. The last steps are repeated till convergence.

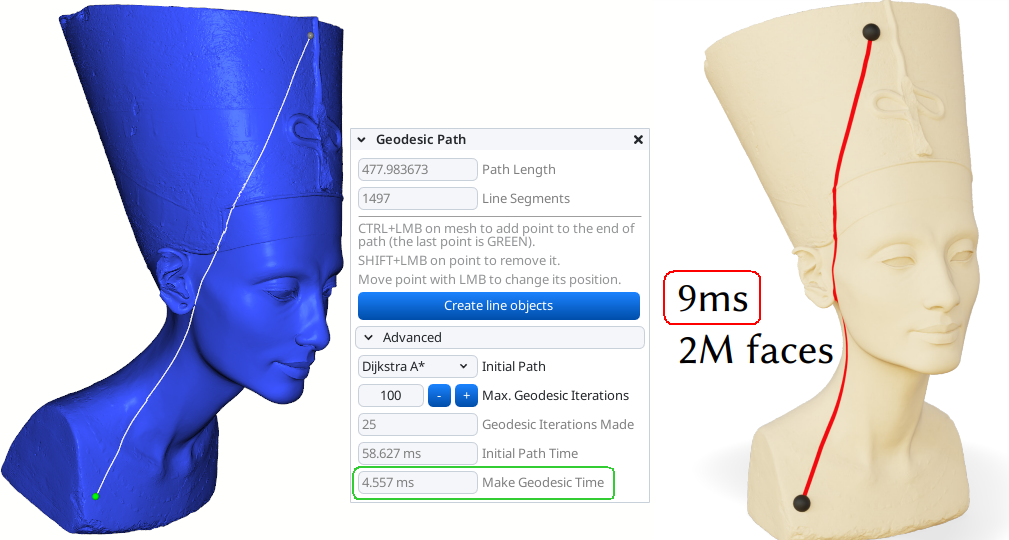
Below is an example of geodesic path on a mesh with 2 million triangles:

• Left - from the application MeshInspector: the time of iterative adjustment is highlighted in green and it is only a small fraction of total time.
• Right - the picture from Just Flipping Edges article, where total time is not given, but it is presumably even higher due to the necessity to construct path network from the mesh.

Ailis

Answer 3

Since your start/end points potentially lie anywhere on the mesh (not restricted to vertices) I guess you are searching for the geodesic shortest path (not Dikstra shortest path following edges). A nice algorithm is implemented in geometry-central: http://geometry-central.net/surface/algorithms/flip_geodesics/

The algorithm is described in the paper "You Can Find Geodesic Paths in Triangle Meshes by Just Flipping Edges".

Bleak