Using MLE function to estimate the parameters of a custom distribution

Question

I am trying to use mle() function in MATLAB to estimate the parameters of a 6-parameter custom distribution.

The PDF of the custom distribution is

and the CDF is

where Γ(x,y) and Γ(x) are the upper incomplete gamma function and the gamma function, respectively. α, θ, β, a, b, and c are the parameters of the custom distribution. K is given by

Given a data vector 'data', I want to estimate the parameters α, θ, β, a, b, and c.

So, far I have come up with this code:

data        =  rand(20000,1); % Since I cannot upload the acutal data, we may use this
t           =  0:0.0001:0.5;    
fun         =  @(w,a,b,c) w^(a-1)*(1-w)^(b-1)*exp^(-c*w);

% to estimate the parameters
custpdf     =  @(data,myalpha,mybeta,mytheta,a,b,c)...
                ((integral(@(t)fun(t,a,b,c),0,1)^-1)*...
                mybeta*...
                igamma(myalpha,((mytheta/t)^mybeta)^(a-1))*...
                (mytheta/t)^(myalpha*mybeta+1)*...
                exp(-(mytheta/t)^mybeta-(c*(igamma(myalpha,(mytheta/t)^mybeta)/gamma(myalpha)))))...
                /...
                (mytheta*...
                gamma(myalpha)^(a+b-1)*...
                (gamma(myalpha)-igamma(myalpha,(mytheta/t)^mybeta))^(1-b));

custcdf     =  @(data,myalpha,mybeta,mytheta,a,b,c)...
                (integral(@(t)fun(t,a,b,c),0,1)^-1)*...
                integral(@(t)fun(t,a,b,c),0,igamma(myalpha,(mytheta/t)^mybeta)^mybeta/gamma(myalpha));

phat        =  mle(data,'pdf',custpdf,'cdf',custcdf,'start',0.0);

But I get the following error:

Error using mlecustom (line 166)
Error evaluating the user-supplied pdf function
'@(data,myalpha,mybeta,mytheta,a,b,c)((integral(@(t)fun(t,a,b,c),0,1)^-1)*mybeta*igamma(myalpha,((mytheta/t)^mybeta)^(a-1))*(mytheta/t)^(myalpha*mybeta+1)*exp(-(mytheta/t)^mybeta-(c*(igamma(myalpha,(mytheta/t)^mybeta)/gamma(myalpha)))))/(mytheta*gamma(myalpha)^(a+b-1)*(gamma(myalpha)-igamma(myalpha,(mytheta/t)^mybeta))^(1-b))'.

Error in mle (line 245)
            phat = mlecustom(data,varargin{:});

Caused by:
    Not enough input arguments.

I tried to look into the error lines but I can't figure out where the error actually is.

Which function lacks fewer inputs? Is it referring to fun? Why would mle lack fewer inputs when it is trying to estimate the parameters?

Could someone kindly help me debug the error?

Thanks in advance.

Dipterocarpaceous

Please paste the error as code (and not an image) so that it can be searchable. Also, there's no need for matlab in the title. – Iceman

@Iceman I made the changes as requested. – Dipterocarpaceous

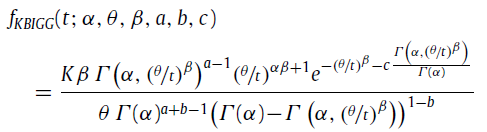
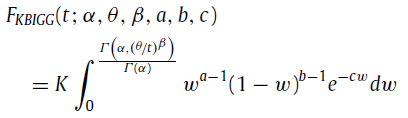
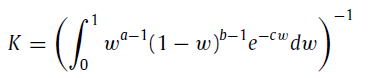
I'm pretty sure the issue is with using your custpdf as the pdf for mle, because mle only provides 2 inputs (see docs) - "This custom function accepts the vector data and one or more individual distribution parameters as input parameters, and returns a vector of cumulative probability values.". If you want to pass more than 2 variables to your function, you should do something like what's shown here. Same goes for custcdf. – Iceman

@Iceman You mean to say that mle(data,'pdf',custpdf,'cdf',custcdf,'start',0.0); should be mle(data,'pdf',@data custpdf(data,myalpha,mybeta,mytheta,a,b,c),'cdf',@data custcdf(data,myalpha,mybeta,mytheta,a,b,c),'start',0.0); – Dipterocarpaceous

Roughly, yes (but with 2 inputs and correct syntax). Regardless - at least in the debugging stage, I would suggest using less anonymous function and more function handles to named functions (e.g. function out = custpdf(...)). Debugging multi-line anonymous functions isn't exactly convenient. – Iceman

@Iceman Okay. I will give it a try. Thanks for the suggestions. – Dipterocarpaceous

Let us continue this discussion in chat. – Dipterocarpaceous

Answer 1

• exp() is a function, not a variable, precise the argument

exp^(-c*w) ---> exp(-c*w)

• The starting point concerns the 6 parameters, not only one 0.1*ones(1,6)
• In custcdf mle requires the upper bound of the integral to be a scalar, I did some trial and error and the range is [2~9]. for the trial some values lead to negative cdf or less than 1 discard them.
• Then use the right one to compute the upper bound see if it's the same as the one you predefined.

I re-write all the functions, check them out

The code is as follow

Censored = ones(5,1);% All data could be trusted 

data        =  rand(5,1); % Since I cannot upload the acutal data, we may use this

f         =  @(w,a,b,c) (w.^(a-1)).*((1-w).^(b-1)).*exp(-c.*w);
% to estimate the parameters
custpdf     =  @(t,alpha,theta,beta, a,b,c)...
                (((integral(@(w)f(w,a,b,c), 0,1)).^-1).*...
                beta.*...
                ((igamma(alpha, (theta./t).^beta)).^(a-1)).*...
                ((theta./t).^(alpha.*beta + 1 )).*...
                exp(-(((theta./t).^beta)+...
                c.*igamma(alpha, (theta./t).^beta)./gamma(alpha))))./...
                (theta.*...
                ((gamma(alpha)).^(a+b-1)).*...
                 ((gamma(alpha)-...
                 igamma(alpha, (theta./t).^beta)).^(1-b)));


custcdf = @(t,alpha,theta,beta, a,b,c)...
         ((integral(@(w)f(w,a,b,c), 0,1)).^-1).*...         
     (integral(@(w)f(w,a,b,c), 0,2));



phat = mle(data,'pdf',custpdf,'cdf',custcdf,'start', 0.1.*ones(1,6),'Censoring',Censored);

Result

    phat = 0.1017    0.1223    0.1153    0.1493   -0.0377    0.0902

Herl

Thank you very much. Your code works very well. May I ask if there is a way to still use the upperbound igamma(myalpha,(mytheta/t)^mybeta)^mybeta/gamma(myalpha). Would using a for loop help? Although there seems to be a problem with passing the data vector. One more thing, can we use phat values to generate the pdf of the custom distribution? That might us to verify if phat are correctly obtained. (I might post this as a separate question) – Dipterocarpaceous

custpdf(data, pheta(1), pheta(2), pheta(3), pheta(4), pheta(5), pheta(6)) could be used to generate the pdf. The upper bound need to be scalar, as you said you can plot the pdf see if it's the right one. Use upper bound = 2, 3.....9and plot the pdf, for your real data it might be different. just try different upper bound if you get errors like cdf is negative then that's the wrong guess. Or error could be cdf has to be greater or equal to 1. – Herl

I tried using custpdf(data, pheta(1), pheta(2), pheta(3), pheta(4), pheta(5), pheta(6)), but I get very different PDFs, which should not be the case. Tried different upper bound of the integral as well but no success. – Dipterocarpaceous