Error in calculating integral for 2D interpolation. Comparing numpy arrays

Question

My optimization task deals with calculation of the following integral and finding the best values of xl and xu:

Iterations take too long, so I decided to speed them up by calculating integral for all possible values xl and xu and then interpolate calculated values during optimization.

I wrote the following function:

def k_integrand(x, xl, xu):
    return((x**2)*mpmath.exp(x))/((xu - xl)*(mpmath.exp(x)-1)**2)
@np.vectorize   
def K(xl, xu):
    y, err = integrate.quad(k_integrand, xl, xu, args = (xl, xu))
    return y

and two identical arrays grid_xl and grid_xu with dinamic increment of values.

When I run the code I get this:

K(grid_xl, grid_xu)
Traceback (most recent call last):

  File "<ipython-input-2-5b9df02f12b7>", line 1, in <module>
    K(grid_xl, grid_xu)

  File "C:/Users/909404/OneDrive/Работа/ZnS-FeS/Теплоемкость/Python/CD357/4 - Optimization CD357 interpolation.py", line 75, in K
    y, err = integrate.quad(k_integrand, xl, xu, args = (xl, xu))

  File "C:\Users\909404\Anaconda3\lib\site-packages\scipy\integrate\quadpack.py", line 323, in quad
    points)

  File "C:\Users\909404\Anaconda3\lib\site-packages\scipy\integrate\quadpack.py", line 372, in _quad
    if (b != Inf and a != -Inf):

ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()

I guess it comes from the fact that xl should be always less than xu. Is there any way to compare the values of xl and xu and return NaN in case if xl>=xu?

In the end I want to have something like this:

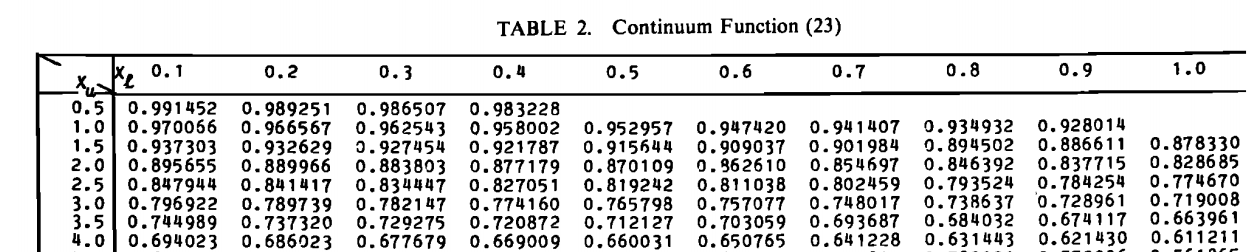
And to have the ability to use interpolation.

Maybe I have chosen the wrong way? I'd appreciate any help.

Lowgrade

What is a and b in your case? Providing the full error traceback would be quite helpful. – Ascending

I have added the full error traceback, hope it helps. – Lowgrade

(b != Inf and a != -Inf) is not possible to evaluate with b and a being arrays of multiple values. Note the source code here, on line 372 onwards; the code decides to use different integration methods depending on whether the bounds a and b is finite or not. In general, unless the _quadpack routines are shown to accept vector arguments, your approach won't work. The parameter description on line 75 and 77 specifically says that a and b need to be floats. – Ascending

Answer 1

I can't reproduce your error unless I omit the np.vectorize decorator. Setting xl/xu values that coincide does give me a ZeroDivisionError though.

Anyway, there's nothing stopping you from checking the values of xu vs xl in your higher-level function. That way you can skip integration entirely for nonsensical data points and return np.nan early:

import numpy as np
import mpmath
import scipy.integrate as integrate

def k_integrand(x, xl, xu):    
    return ((x**2)*mpmath.exp(x))/((xu - xl)*(mpmath.exp(x)-1)**2)

@np.vectorize   
def K(xl, xu):
    if xu <= xl:
        # don't even try to integrate
        return np.nan
    y, err = integrate.quad(k_integrand, xl, xu, args = (xl, xu))
    return y

grid_xl = np.linspace(0.1,1,10)        # shape (10,) ~ (1,10)
grid_xu = np.linspace(0.5,4,8)[:,None] # shape (8,1)

With these definitions I get (following np.set_printoptions(linewidth=200) for easier comparison:

In [35]: K(grid_xl, grid_xu)
Out[35]: 
array([[0.99145351, 0.98925197, 0.98650808, 0.98322919,        nan,        nan,        nan,        nan,        nan,        nan],
       [0.97006703, 0.96656815, 0.96254363, 0.95800307, 0.95295785, 0.94742104, 0.94140733, 0.93493293, 0.9280154 ,        nan],
       [0.93730403, 0.93263063, 0.92745487, 0.92178832, 0.91564423, 0.90903747, 0.90198439, 0.89450271, 0.88661141, 0.87833062],
       [0.89565597, 0.88996696, 0.88380385, 0.87717991, 0.87010995, 0.8626103 , 0.85469862, 0.84639383, 0.83771595, 0.82868601],
       [0.84794429, 0.8414176 , 0.83444842, 0.82705134, 0.81924245, 0.81103915, 0.8024601 , 0.79352503, 0.7842547 , 0.77467065],
       [0.79692339, 0.78974   , 0.78214742, 0.77416128, 0.76579857, 0.75707746, 0.74801726, 0.73863822, 0.72896144, 0.71900874],
       [0.7449893 , 0.73732055, 0.7292762 , 0.72087263, 0.71212741, 0.70305921, 0.69368768, 0.68403329, 0.67411725, 0.66396132],
       [0.69402415, 0.68602325, 0.67767956, 0.66900991, 0.66003222, 0.65076537, 0.6412291 , 0.63144388, 0.62143077, 0.61121128]])

You can see that the values perfectly agree with your linked image.

Now, I've got bad news and good news. The bad news is that while np.vectorize provides syntactical sugar around calling your scalar integration function with array inputs, it won't actually give you speed-up compared to a native for loop. The good news is that you can replace the calls to mpmath.exp with calls to np.exp and you'll end up with the same result much faster:

def k_integrand_np(x, xl, xu):    
    return ((x**2)*np.exp(x))/((xu - xl)*(np.exp(x)-1)**2)

@np.vectorize   
def K_np(xl, xu):
    if xu <= xl:
        # don't even try to integrate
        return np.nan
    y, err = integrate.quad(k_integrand_np, xl, xu, args = (xl, xu))
    return y

With these definitions

In [14]: res_mpmath = K(grid_xl, grid_xu)
    ...: res_np = K_np(grid_xl, grid_xu)
    ...: inds = ~np.isnan(res_mpmath)
    ...: 

In [15]: np.array_equal(res_mpmath[inds], res_np[inds])
Out[15]: True

In [16]: %timeit K(grid_xl, grid_xu)
107 ms ± 521 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

In [17]: %timeit K_np(grid_xl, grid_xu)
7.26 ms ± 157 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

So the two methods give the same result (exactly!), but the numpy version is almost 15 times faster.

Chopping

Thank you, it really helped! I've managed to speed up my calculations by rewriting my initial integrand using np.sinh() function and added 'if' statement to K_np like you proposed. – Lowgrade

Answer 2

Using a low-level callback function for integration

The following answer is meant as a comment to @Andras Deak answer, but is to long for a comment.

The scipy integrate functions call the k_integrand_np function multiple times, which is quite slow. The alternative of using a pure Python function is to use a low-level callback function. This function can be written directly in C or in Python using a compiler like Numba. The following is a slightly modified version of this answer.

Example

import time
import numpy as np
import numba
import scipy.integrate as integrate
from scipy import LowLevelCallable
from numba import cfunc
from numba.types import intc, CPointer, float64


##wrapper for a function that takes 3 input values
def jit_integrand_function(integrand_function):
    jitted_function = numba.njit(integrand_function)
    
    @cfunc(float64(intc, CPointer(float64)))
    def wrapped(n, xx):
        return jitted_function(xx[0], xx[1],xx[2])
    return LowLevelCallable(wrapped.ctypes)

#your function to integrate
def k_integrand_np(x, xl, xu):
  return ((x**2)*np.exp(x))/((xu - xl)*(np.exp(x)-1)**2)

#compile integrand
k_integrand_nb=jit_integrand_function(k_integrand_np)

#now we can use the low-level callable
@np.vectorize
def K_nb(xl, xu):
    if xu <= xl:
        # don't even try to integrate
        return np.nan
    y, err = integrate.quad(k_integrand_nb, xl, xu, args = (xl, xu))
    return y

#for comparison
@np.vectorize
def K_np(xl, xu):
    if xu <= xl:
        # don't even try to integrate
        return np.nan
    y, err = integrate.quad(k_integrand_np, xl, xu, args = (xl, xu))
    return y

Performance

#create some data
grid_xl = np.linspace(0.1,1,500)      
grid_xu = np.linspace(0.5,4,800)[:,None] 

t1=time.time()
res_nb = K_nb(grid_xl, grid_xu)
print(time.time()-t1)
t1=time.time()
res_np = K_np(grid_xl, grid_xu)
print(time.time()-t1)

inds = ~np.isnan(res_nb)
np.allclose(res_nb[inds], res_np[inds])

K_np: 24.58s
K_nb: 0.97s (25x speedup)
allclose: True

Diplomatist

Nice job. I wonder; don't the arrays equal exactly? I suspect it's easily possible that they do, since numba-compiling should not necessarily affect the order of operations, so floating-point errors could be the same between the two methods. I also wonder if this speedup is enough to solve OP's original problem directly. – Willful

No, they are not exactly the same. I don't know really why this happens, but I suspect that Numba simplifies x**2 (or np.power(x,2)) to x*x which may not be the same in terms of precision but quite a lot faster. On SIMD-vectorized operations precision may also vary numba.pydata.org/numba-doc/dev/user/performance-tips.html – Diplomatist