Number of combinations with LEGO plastic bricks C++

Question

You have some LEGO plastic bricks, all bricks are 1x1x1. Also you have one tile, 1xN (N <= 80), on which you should place the LEGO bricks. You can order them in sequences (one sequence is correct if it has 3 or more consecutive bricks), also you must have at least 1 empty space between 2 sequences. You should calculate the number of different combination you can place the bricks on the tiles.

Here's an example:

If the tile is 1x7, there are 17 different combinations.

input : 7 output : 17

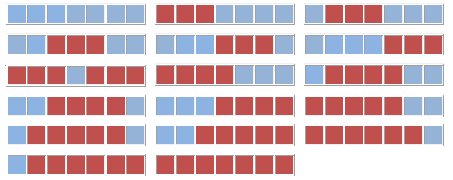
_{(source: mendo.mk)}

Also if you have no bricks it's counted as 1 combination.

I have worked on this problem and i found the way to calculate possible combinations of if the max length of the tile is 14 (3 sequences). I found it using for loops.

My biggest problem is the huge number of for loops that i need to run. For example, for 1 sequence i use 1 for loops, for 2 sequences 2 loops + 1 for 1 sequnce...so if i use all 80 bricks, i can create 20 sequence and i will have to use over 210 for loops which is huge number. So it'll be good if i can nest them in one. I tried it and it get messy and it doesn't give correct answers.

New code:

#include <iostream>
using namespace std;
int main()
{
    long long int places, combinations = 1;
    cin >> places;
    long long int f[80], g[80];
    f[0] = 0;
    f[1] = 0;
    f[2] = 0;
    g[0] = 1;
    g[1] = 1;
    g[2] = 1;
    for(int i = 3; i<=places; i++)
    {
        f[i] = f[i-1] + g[i-3];
        g[i] = f[i-1] + g[i-1];
    }
    combinations = f[places] + g[places];
    cout << combinations;
    return 0;
}

Purulent

you can use class by witch you only need to do this for only one time then use class again and again – Andino

I don't really know how it will help me, also i don't have expirience with class, so please post a little example. if you didn't noticed the algorithm for 1 sequence is different from the one for 2 and so on – Purulent

can you explain this? also you must have at least 1 empty space between 2 sequences. Your example is not in coherence with this statement – Multiversity

in the following example X is a brick and @ is empty space For example in 1x7 tile: XXX@XXX is valid one with 2 sequence – Purulent

@Purulent in your example i found in bottom three row that there is not1 empty space between 2 sequences? would you mind explain – Andino

Algorithmically speaking, I can't help noticing that the presence or otherwise of a brick is a bit of a binary state, and you basically shift patterns along... :-) – Driving

@Mayank I think there must be 3 or more red bricks in a row to be valid. If there is more than one sequence, it must have at least a 1 brick gap. There is only one example of 2 sequences in the OP (first of row 3) – Paigepaik

Yes, there is no empty space, but it's only 1 sequence, if you read the post carefully, i wrote that correct sequence is one that is build from 3 or more consecutive bricks, so in the last 3 rows there is only 1 sequence, made from 4, 5, 6 and bricks – Purulent

@user1158692 how can i shift all the pattern? If i have 1x80 tile there is billions of combination, it's such a huge number. Also how can i check if it complete the condition? – Purulent

There are 2^N patterns of bricks. Invalid patterns contain a series of 1 or 2 1's. It may be easier to eliminate the invalid patterns than generate the valid ones. – Stickybeak

It sounds like you need a recursive algorithm instead of a variable number of for loops. – Helicline

surely there is a mathematical solution to this that requires no loops? – Hammerskjold

Answer 1

If this is a counting problem (not outputting combination, rather just counting them) it's an easy one. Assume we solved it for n ≥ 3 now to solve it for n+1, we solve it by induction:

Assume f is a function that shows the number of possible ways such that the last item is a brick. Analogously g is a function that shows the number of possible ways such that the last item is not brick. Let define h = f+g, to be the number of all possible ways.

So we have:

f(n+1) = f(n) + g(n-2)
g(n+1) = g(n) + f(n)

With initial condition:

for n=0,1,2: g=1, f= 0.
for n = 3: g=1,f=1

Samples:

n=4: g=2,f=2 ==> h=4
n=5: g=4, f= 3 ==> h=7
n=6: g=7, f= 4 ==> h=11
n=7: g=11,f=6 ==> h=17

We can solve it with one for loop in O(n).

---

Why:

f(n+1) = f(n) + g(n-2)
g(n+1) = g(n) + f(n)

First, let prove first part:

Remember that we assumed f(n) is a working solution which has a plastic brick in the last item, and g(n) is a working solution which doesn't have a brick in the last item.

f(n+1) can be obtained from f(n) by adding one brick at the last place. Also f(n+1) can be obtained by adding three brick after g(n-2), it means cells of n-1,n,n+1.

Note that we can't add brick after g(n-1) or g(n) to create a valid solution for f(n+1) because they are not valid solutions (number of consecutive bricks is less than 3). Also, note that we don't need to count the number of ways which arises by adding bricks after g(n-3) because they are previously enumerated by f(n). So we have f(n+1) = f(n) + g(n-2).

In the same way we can prove g(n+1) = f(n)+g(n) this case is easier, because g(n+1) simply can be made from any valid solution up to n, as there is no 3 consecutive brick barrier here, they can come after any valid solution.

Ascot

It's interesting method. I tried it for some values and it works, but please tell me how did you find this out: f(n+1) = f(n) + g(n-2) g(n+1) = g(n) + f(n) – Purulent

@Stefan4024, see my update. I think it's enough, if you want more think yourself :) but if there is something wrong with my update please tell me to edit it. – Ascot

I have little problem check it, i upload the new code on the first post, please tell me where i'm wrong. Anyway. thank you very much Saeed – Purulent

@Stefan4024, because your f and g are int you can use int64 instead. number is big and will overflow. – Ascot

how can i be so stupid :S. I did it to combinations and forgot to do the same on f and g. Thank you veru much – Purulent

Answer 2

As a person with math training, rather than CS, I feel obliged to mention that, while Saeed Amiri's algorithm is very nice and would probably work fast enough for N up to a few millions (with constant memory, of course), there is a better algorithm from the time perspective.

I will pick up where he has left:

f(n+1) = f(n) + g(n-2)
g(n+1) = f(n) + g(n)

Since f and g are discrete functions, you can treat them as sequences. This becomes a linear system of recurrence relations, then. Luckily, a system like this can be completely solved, so that the explicit form of f and g can be presented.
Unfortunately, SO does not seem to support MathJax like math.SE, so I apologize for the low quality of the equations from here on.
Let

     | f(n) |
     |f(n-1)|
u(n)=|f(n-2)|
     | g(n) |
     |g(n-1)|
     |g(n-2)|

That is, u(n) is a vector row. Then, the following is true:

|f(n+1)|   |1 0 0 0 0 1|   | f(n) |
| f(n) |   |1 0 0 0 0 0|   |f(n-1)|
|f(n-1)| = |0 1 0 0 0 0| . |f(n-2)|
|g(n+1)|   |1 0 0 1 0 0|   | g(n) |
| g(n) |   |0 0 0 1 0 0|   |g(n-1)|
|g(n-1)|   |0 0 0 0 1 0|   |g(n-2)|

What follows from this is, that u(n) = A * u(n-1), where A is the matrix above.
Then, u(n) = (A^(n-2)) * u(2), where u(2) is the vector, containing the initial values to the problem. This, in turn, gives an algorithm with O(log(n)) complexity, since you can use fast exponentiation to calculate (A^(n-2)) and then multiply it to u(2).

Of course, any such technique would probably require a BigInt of some sort, since otherwise the overflow is pretty much guaranteed.

Also note that this technique can be applied one step further:
You can find the eigenvectors and eigenvalues of A and then decompose u(2) into the eigenvectors. Then, you will have a closed form for both f(n) and g(n).

I strongly advise you against an algorithm based on the closed form
It almost certainly will involve high-precision floating-point calculations (unless all eigenvalues are integers, which is highly unlikely), which are of at least this complexity from programming perspective, and are not generally constant-time operations. Of course, neither are BigInt operations. So a constant-time algorithm is generally not feasible, plus you probably do not even need the O(log(n)), since for most uses the linear is good enough.

Note
The technique described here can be used in a variety of problems and is of extreme use in dynamic optimization problems. Plus, usually people are pretty impressed when they see this for the first time ;)

Harriet

+1, Actually I thought to solve the recursion equation with generator function, but normally this is out of this site principles, and as you mentioned floating point problem can be happen, Also dealing with bigInt is same in both of us algorithms, f,g growing exponentially and I think this algorithm wont work for n>100 :) – Ascot

@SaeedAmiri I agree, what I meant with "the algorithm will work for up to a few million" is that its runtime would be reasonable and would not consume too much CPU-seconds. Otherwise, this sequence is exponential and would probably overflow about 100 (or may be even less), so yeap, BigInt is a common element :) – Harriet

rewriting the equation you can express g(n) as 2*g(n-1)-g(n-2)+g(n-4). From this -> oeis.org/A005252 and the closed form is: g(n)=(((1+sqrt(5))/2)^(n+1)/sqrt(5)-((1-sqrt(5))/2)^(n+1)/sqrt(5)+cos(pin/3)+sin(pin/3)/sqrt(3))/2 . lovely 8) – Itch