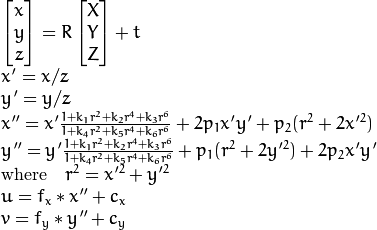Understanding of openCV undistortion

Question

I'm receiving depth images of a tof camera via MATLAB. the delivered drivers of the tof camera to compute x,y,z coordinates out of the depth image are using openCV function, which are implemented in MATLAB via mex-files.

But later on I can't use those drivers anymore nor use openCV functions, therefore I need to implement the 2d to 3d mapping on my own including the compensation of radial distortion. I already got hold of the camera parameters and the computation of the x,y,z coordinates of each pixel of the depth image is working. Until now I am solving the implicit equations of the undistortion via the newton method (which isn't really fast...). But I want to implement the undistortion of the openCV function.

... and there is my problem: I dont really understand it and I hope you can help me out there. how is it actually working? I tried to search through the forum, but havent found any useful threads concerning this case.

greetings!

Zibet

Answer 1

The equations of the projection of a 3D point [X; Y; Z] to a 2D image point [u; v] are provided on the documentation page related to camera calibration :

_{(source: opencv.org)}

In the case of lens distortion, the equations are non-linear and depend on 3 to 8 parameters (k1 to k6, p1 and p2). Hence, it would normally require a non-linear solving algorithm (e.g. Newton's method, Levenberg-Marquardt algorithm, etc) to inverse such a model and estimate the undistorted coordinates from the distorted ones. And this is what is used behind function undistortPoints, with tuned parameters making the optimization fast but a little inaccurate.

However, in the particular case of image lens correction (as opposed to point correction), there is a much more efficient approach based on a well-known image re-sampling trick. This trick is that, in order to obtain a valid intensity for each pixel of your destination image, you have to transform coordinates in the destination image into coordinates in the source image, and not the opposite as one would intuitively expect. In the case of lens distortion correction, this means that you actually do not have to inverse the non-linear model, but just apply it.

Basically, the algorithm behind function undistort is the following. For each pixel of the destination lens-corrected image do:

• Convert the pixel coordinates (u_dst, v_dst) to normalized coordinates (x', y') using the inverse of the calibration matrix K,
• Apply the lens-distortion model, as displayed above, to obtain the distorted normalized coordinates (x'', y''),
• Convert (x'', y'') to distorted pixel coordinates (u_src, v_src) using the calibration matrix K,
• Use the interpolation method of your choice to find the intensity/depth associated with the pixel coordinates (u_src, v_src) in the source image, and assign this intensity/depth to the current destination pixel.

Note that if you are interested in undistorting the depthmap image, you should use a nearest-neighbor interpolation, otherwise you will almost certainly interpolate depth values at object boundaries, resulting in unwanted artifacts.

Pulchritude

thanks for your reply, I have already read about such an approach. but I dont really get it. why should I distort the already distorted normalized coordinates? on what assumption is it applied? Could you provide more detailed information about this step? – Zibet

"why should I distort the already distorted normalized coordinates?" > actually, you convert pixel coordinates from the undistorted image (u_dst, v_dst) to pixel coordinates from the distorted image (u_src, v_src), in order to retrieve the intensity/depth to be assigned to the undistorted pixel. – Pulchritude

Ok thx.. I think, I'm understanding the idea behind it. but if I do so, wont I neglect a certain amount of depth values at the image border? – Zibet

Not necessarily, since you can build your destination image as you wish : you can increase its size and change the origin if you take it into account when you do the mapping to normalized coordinates. – Pulchritude

ok thanks so far! For the further processing I just need the x,y,z coordinates of the pixels. before I'm going to decide, which inverse modelation I will implement, can you tell me, how the optimization of the function undistortPoints works? – Zibet

I mentioned it in my answer, though I'm not sure what non-linear optimisation variant is implemented. You can study the implementation in file undistort.cpp from imgproc module. – Pulchritude

ok thanks! do you remember any (academic) article/reference on which the tuning of the parameters is based in undistort.cpp? – Zibet

I don't think there's an article for that, it is just a tuning of the number of iterations and threshold accuracy for the iterative method, in order to match the tradeoff between speed and accuracy for your needs. If you want high accuracy, you can have a look at code.google.com/p/ceres-solver, which is a light-weight and powerful non-linear solver easy to get started with. – Pulchritude

Answer 2

The above answer is correct, but do note that UV coordinates are in screen space and centered around (0,0) instead of "real" UV coordinates.

Source: own re-implementation using Python/OpenGL. Code:

def correct_pt(uv, K, Kinv, ds):
   uv_3=np.stack((uv[:,0],uv[:,1],np.ones(uv.shape[0]),),axis=-1)
   [email protected]
   r=np.linalg.norm(xy_,axis=-1)
   coeff=(1+ds[0]*(r**2)+ds[1]*(r**4)+ds[4]*(r**6));
   xy__=xy_*coeff[:,np.newaxis]
   return ([email protected])[:,0:2]

Quianaquibble