Turing machine for addition and comparison of binary numbers

Question

Good Day everyone!

I am trying to solve this Exercise for learning purpose. Can someone guide me in solving these 3 questions?

Like I tried the 1st question for addition of 2 binary numbers separated by '+'. where I tried 2 numbers addition by representing each number with respective number of 1's or zeros e.g 5 = 1 1 1 1 1 or 0 0 0 0 0 and then add them and the result will also be in the same format as represented but how to add or represent 2 binaries and separating them by +, not getting any clue. Will be head of Turing machine move from left and reach plus sign and then move left and right of + sign? But how will the addition be performed. As far as my little knowledge is concerned TM can not simply add binaries we have to make some logic to represent its binaries like in the case of simple addition of 2 numbers. Similar is the case with comparison of 2 binaries? Regards

Extempore

Answer 1

I'll start with problems 2 and 3 since they are actually easier than problem 1.

We'll assume we have valid input (non-empty binary strings on both sides with no leading zeroes), so we don't need to do any input validation. To check whether the numbers are equal, we can simply bounce back and forth across the = symbol and cross off one digit at a time. If we find a mismatch at any point, we reject. If we have a digit remaining on the left and can't find one on the right, we reject. If we run out of digits on the left and still have some on the right, we reject. Otherwise, we accept.

Q    T    Q'    T'    D

q0   0    q1    X     right    // read the next (or first) symbol
q0   1    q2    X     right    // of the first binary number, or
q0   =    q7    =     right    // recognize no next is available

q1   0    q1    0     right    // skip ahead to the = symbol while 
q1   1    q1    1     right    // using state to remember which
q1   =    q3    =     right    // symbol we need to look for
q2   0    q2    0     right
q2   1    q2    1     right
q2   =    q4    =     right

q3   X    q3    X     right    // skip any crossed-out symbols
q3   0    q5    X     left     // in the second binary number
q3   1,b  rej   1     left     // then, make sure the next
q4   X    q4    X,b   right    // available digit exists and
q4   0,b  rej   0,b   left     // matches the one remembered
q4   1    q5    X     left     // otherwise, reject

q5   X    q5    X     left     // find the = while ignoring
q5   =    q6    =     left     // any crossed-out symbols

q6   0    q6    0     left     // find the last crossed-out
q6   1    q6    1     left     // symbol in the first binary
q6   X    q0    X     right    // number, then move right
                               // and start over

q7   X    q7    X     right    // we ran out of symbols
q7   b    acc   b     left     // in the first binary number,
q7   0,1  rej   0,1   left     // make sure we already ran out
                               // in the second as well

This TM could first sanitize input by ensuring both binary strings are non-empty and contain no leading zeroes (crossing off any it finds).

Do to "greater than", you could easily do the following:

1. check to see if the length of the first binary number (after removing leading zeroes) is greater than, equal to, or less than the length of the second binary number (after removing leading zeroes). If the first one is longer than the second, accept. If the first one is shorter than the second, reject. Otherwise, continue to step 2.

2. check for equality as in the other problem, but accept if at any point you have a 1 in the first number and find a 0 in the second. This works because we know there are no leading zeroes, the numbers have the same number of digits, and we are checking digits in descending order of significance. Reject if you find the other mismatch or if you determine the numbers are equal.

To add numbers, the problem says to increment and decrement, but I feel like just adding with carry is going to be not significantly harder. An outline of the procedure is this:

1. Begin with carry = 0.
2. Go to least significant digit of first number. Go to state (dig=X, carry=0)
3. Go to least significant digit of second number. Go to state (sum=(X+Y+carry)%2, carry=(X+Y+carry)/2)
4. Go after the second number and write down the sum digit.
5. Go back and continue the process until one of the numbers runs out of digits.
6. Then, continue with whatever number still has digits, adding just those digits and the carry.
7. Finally, erase the original input and copy the sum backwards to the beginning of the tape.

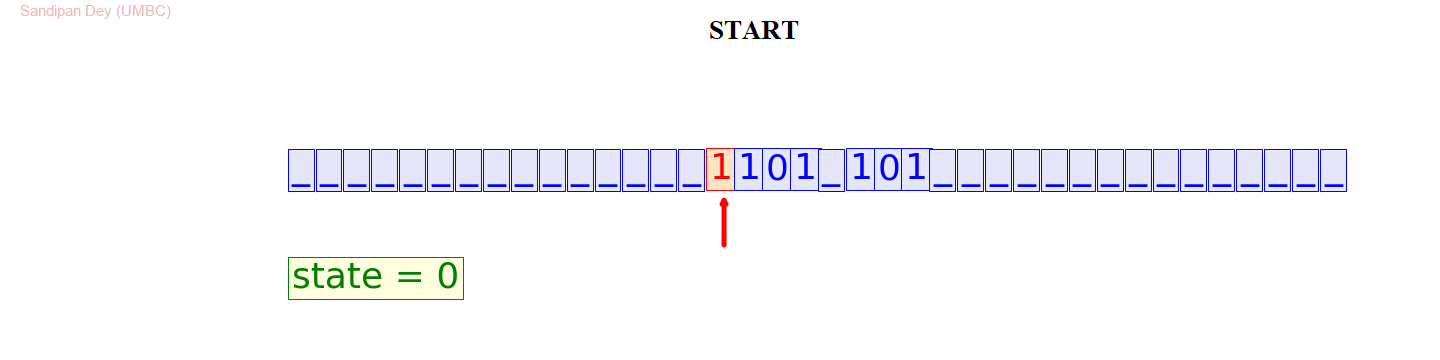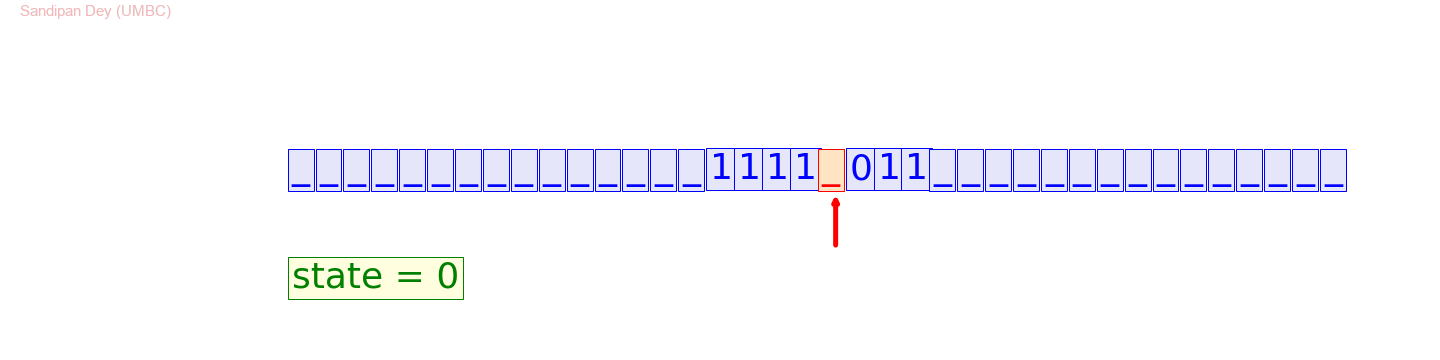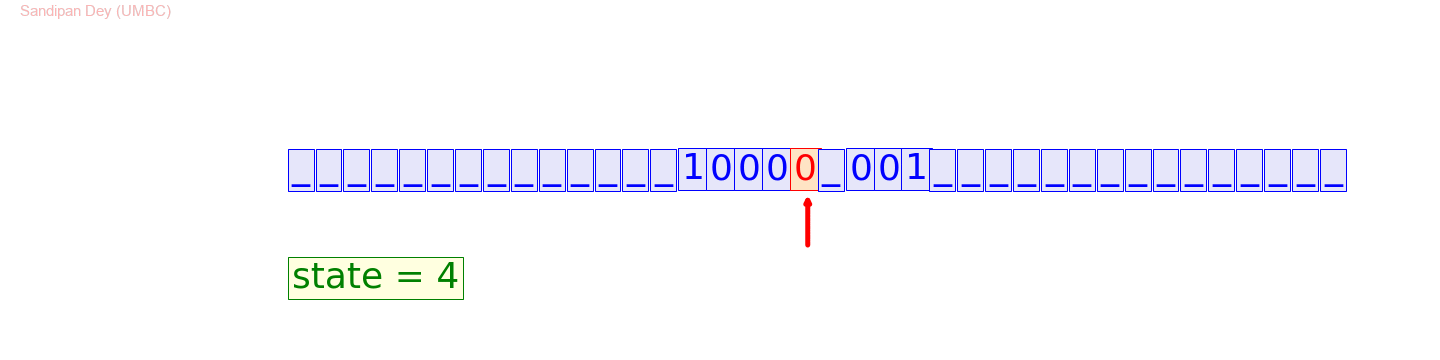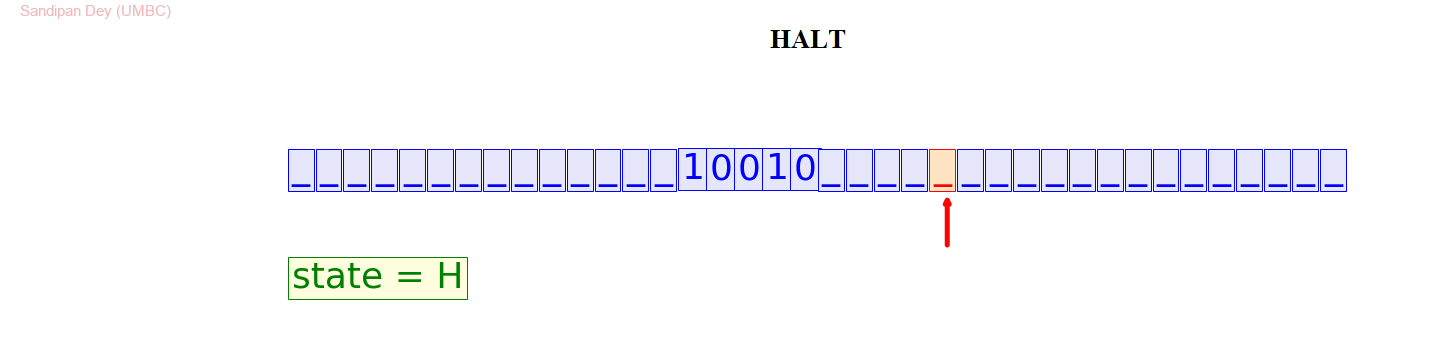
An example of the distinct steps the tape might go through:

#1011+101#
#101X+101#
#101X+10X#
#101X+10X=#
#101X+10X=0#
#10XX+10X=0#
#10XX+1XX=0#
#10XX+1XX=00#
#1XXX+1XX=00#
#1XXX+XXX=00#
#1XXX+XXX=000#
#XXXX+XXX=000#
#XXXX+XXX=0000#
#XXXX+XXX=00001#
#XXXX+XXX=0000#
#1XXX+XXX=0000#
#1XXX+XXX=000#
#10XX+XXX=000#
#10XX+XXX=00#
#100X+XXX=00#
#100X+XXX=0#
#1000+XXX=0#
#1000+XXX=#
#10000XXX=#
#10000XXX#
#10000XX#
#10000X#
#10000#

Mayers

Answer 2

The following program, inspired by the edX / MITx course Paradox and Infinity, shows how to perform binary addition with a Turing machine, where the numbers to be added are input to the Turing machine and are separated by a blank.

The Turing Machine

• uses the second number as a counter
• decrements the second number by one
• increments the first number by one

till the second number becomes 0.

The following animation of the simulation of the Turing machine shows how 13 (binary 1101) and 5 (binary 101) are added to yield 18 (binary 10010).

Cookshop

Answer 3

There are two ways to solve the addition problem. Assume your input tape is in the form ^a+b$, where ^ and $ are symbols telling you you've reached the front and back of the input.

1. You can increment b and decrement a by 1 each step until a is 0, at which point b will be your answer. This is assuming you're comfortable writing a TM that can increment and decrement.
2. You can implement a full adding TM, using carries as you would if you were adding binary numbers on paper.

For either option, you need code to find the least significant bit of both a and b. The problem specifies that the most significant bit is first, so you'll want to start at + for a and $ for b.

For example, let's say we want to increment 1011$. The algorithm we'll use is find the least significant unmarked digit. If it's a 0, replace it with a 1. If it's a 1, move left.

1. Start by finding $, moving the read head there. Move the read head to the left.
2. You see a 1. Move the read head to the left.
3. You see a 1. Move the read head to the left.
4. You see a 0. write 1.
5. Return the read head to $. The binary number is now 1111$.

To compare two numbers, you need to keep track of which values you've already looked at. This is done by extending the alphabet with "marked" characters. 0 could be marked as X, 1 as Y, for example. X means "there's a 0 here, but I've seen it already.

So, for equality, we can start at ^ for a and = for b. (Assuming the input looks like ^a=b$.) The algorithm is to find the start of a and b, comparing the first unmarked bit of each. The first time you get to a different value, halt and reject. If you get to = and $, halt and reject.

Let's look at input ^11=10$:

1. Read head starts at ^.
2. Move the head right until we find an unmarked bit.
3. Read a 1. Write Y. Tape reads ^Y1=10$. We're in a state that represents having read a 1.
4. Move the head right until we find =.
5. Move the head right until we find an unmarked bit.
6. Read a 1. This matches the bit we read before. Write a Y.
7. Move the head left until we find ^.
8. Go to step 2.
9. This time, we'll read a 1 in a and read the 0 in b. We'll halt and reject.

Hope this helps to get you started.

Chongchoo

thanks @Chongchoo for the detailed answer. Just a little more help In the 3rd question how we can compare and read when the first number is greater than the second number. Only then we can accept and reject according to the requirement of question.? regards – Extempore

so we have to compare both sides e.g comparing 10101 = 11111 we compare individually each left hand side of the = if left side digit is less than right side digit then we reject. 10101 = 11111 in this example on second comparison the string gets rejected. right ? – Extempore