Python iterate through connected components in grayscale image

Question

I have a gray scale image with values between 0 (black) and white (255). I have a target matrix of the same size as the gray scale image. I need to start at a random pixel in the gray scale image and traverse through the image one pixel at a time (in a depth-first search manner), copying its value to the corresponding location in the target matrix. I obviously need to do this only for the non-white pixels. How can I do this? I thought that I could get the connected components of the gray scale image and traverse each pixel one by one, but I couldn't find any suitable implementation of connected components. Any ideas?

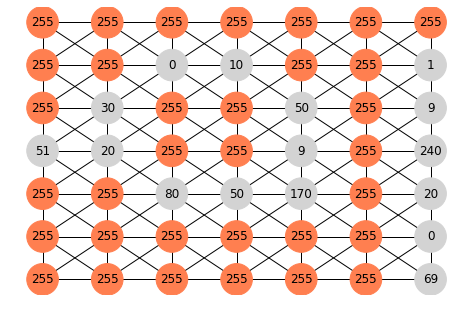
For example, if my gray scale image is:

[[255,255,255,255,255,255,255]
[255,255, 0 ,10 ,255,255, 1 ]
[255,30 ,255,255,50 ,255, 9 ]
[51 ,20 ,255,255, 9 ,255,240]
[255,255,80 ,50 ,170,255, 20]
[255,255,255,255,255,255, 0 ]
[255,255,255,255,255,255, 69]]

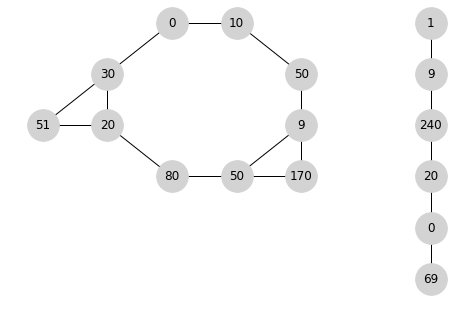
Then a possible traversal is [0,10,50,9,170,50,80,20,51,30] followed by [1,9,240,20,0,69] to give [0,10,50,9,170,50,80,20,51,30,1,9,240,20,0,69]. The order between the different objects doesn't matter.

Other possible traversals are: [1,9,240,20,0,69,0,10,50,9,170,50,80,20,51,30] or [1,9,240,20,0,69,0,10,50,9,170,50,80,20,30,51] or [1,9,240,20,0,69,10,50,9,170,50,80,20,30,0,51]

etc.

Spicy

Could you add some example data? I read the question now 5 times and I don't see the problem of using two nested for loops with a random start and excluding by copying only values != 255. Maybe specify the question a bit more. – Procter

Added an example. I can't just copy non-255 values because that wouldn't be depth-first search – Spicy

Your example has values between 0 and 1 and in question, you are saying the grayscale image has values between 0 and 255. Also, why do you require dfs? – Ralli

I perceive "depth first" to mean you go down a hierarchy of, say, directories first before worrying about the contents of each directory. What do you mean in a flat, non-hierarchical image by "depth first"? – Rolfston

@KartikeySingh fixed the example! – Spicy

@MarkSetchell yes. In this case, by depth first I mean this: start at a pixel and traverse adjoining pixels in a depth first manner (i.e. continue to just go to any connected pixel and keep going until a pixel has no more unvisited connected pixels. Then go back to previous pixels and see if they have any unvisited neighbours and continue this process till all non-white pixels have been visited) – Spicy

I still don't understand what you mean by "depth first" and your example is poor because there is only one "object" in the image and it is only one pixel thick so there is little choice about which pixel to take next. Maybe you could add a diagram with 2 fatter objects and number the order to copy across, or draw a line tracing out the order. Thanks. – Rolfston

I believe OP is trying to explain that he actually wants to search a path in a maze using a depth-first approach where the path is defined by black pixels. – Colburn

@MarkSetchell added. – Spicy

@Dawid, yes but not only black pixels. Any non-white pixels. – Spicy

I still don't understand. If your first pixel is 240 and the second one is 9, can the third one be 20? – Rolfston

No, that is not depth-first search. Think about the depth-first search algorithm for a graph – Spicy

So, your example presumably corresponds to the digits 01? Have you managed to at least write the code that splits the 0 from the 1? Where's that please? – Rolfston

Please tell me a possible traversal beginning with 240. – Rolfston

240,9,1,20,0,69,0,10,50,9,170,50,80,20,51,30 – Spicy

I had the same problem with poor documentations of connected component. Actually networkx has a pretty good one but performance is really slow and unsatisfactory for me. Then I have found a solution using igraph. I'm going to describe it asap. – Daile

Answer 1

You can use networkx:

from itertools import product, repeat
import numpy as np
import networkx as nx

arr = np.array(
[[255,255,255,255,255,255,255],
 [255,255, 0 ,10 ,255,255, 1 ],
 [255,30 ,255,255,50 ,255, 9 ],
 [51 ,20 ,255,255, 9 ,255,240],
 [255,255,80 ,50 ,170,255, 20],
 [255,255,255,255,255,255, 0 ],
 [255,255,255,255,255,255, 69]])

# generate edges
shift = list(product(*repeat([-1, 0, 1], 2)))
x_max, y_max = arr.shape
edges = []

for x, y in np.ndindex(arr.shape):
    for x_delta, y_delta in shift:
        x_neighb = x + x_delta
        y_neighb = y + y_delta
        if (0 <= x_neighb < x_max) and (0 <= y_neighb < y_max):
            edge = (x, y), (x_neighb, y_neighb)
            edges.append(edge)

# build graph
G = nx.from_edgelist(edges)

# draw graph
pos = {(x, y): (y, x_max-x) for x, y in G.nodes()}
nx.draw(G, with_labels=True, pos=pos, node_color='coral', node_size=1000)

# draw graph with numbers
labels = dict(np.ndenumerate(arr))
node_color = ['coral' if labels[n] == 255 else 'lightgrey' for n in G.nodes()]
nx.draw(G, with_labels=True, pos=pos, labels=labels, node_color=node_color, node_size=1000)

# build subgraph
select = np.argwhere(arr < 255)
G1 = G.subgraph(map(tuple, select))

# draw subgraph
pos = {(x, y): (y, x_max-x) for x, y in G1.nodes()}
labels1 = {n:labels[n] for n in G1.nodes()}
nx.draw(G1, with_labels=True, pos=pos, labels=labels1, node_color='lightgrey', node_size=1000)

# find connected components and DFS trees
for i in nx.connected_components(G1):
    source = next(iter(i))
    idx = nx.dfs_tree(G1, source=source)
    print(arr[tuple(np.array(idx).T)])

Output:

[  0  10  50   9  50  80  20  30  51 170]
[  9   1 240  20   0  69]

Kitchenmaid

That looks very elegant! – Rolfston

Answer 2

So after so much researches for suitable implementation of connected components, I came up with my solution. In order to reach the best I can do in terms of performance, I relied on these rules:

1. Not to use networkx because it's slow according to this benchmark
2. Use vectorized actions as much as possible because Python based iterations are slow according to this answer.

I'm implementing an algorithm of connected components of image here only because I believe this is an essential part of this question.

Algorithm of connected components of image

import numpy as np
import numexpr as ne
import pandas as pd
import igraph

def get_coords(arr):
    x, y = np.indices(arr.shape)
    mask = arr != 255
    return  np.array([x[mask], y[mask]]).T

def compare(r1, r2):
    #assuming r1 is a sorted array, returns:
    # 1) locations of r2 items in r1
    # 2) mask array of these locations
    idx = np.searchsorted(r1, r2)
    idx[idx == len(r1)] = 0
    mask = r1[idx] == r2
    return idx, mask

def get_reduction(coords, s):
    d = {'s': s, 'c0': coords[:,0], 'c1': coords[:,1]}
    return ne.evaluate('c0*s+c1', d)

def get_bounds(coords, increment):
    return np.max(coords[1]) + 1 + increment

def get_shift_intersections(coords, shifts):
    # instance that consists of neighbours found for each node [[0,1,2],...]
    s = get_bounds(coords, 10)
    rdim = get_reduction(coords, s)
    shift_mask, shift_idx = [], []
    for sh in shifts:
        sh_rdim = get_reduction(coords + sh, s)
        sh_idx, sh_mask = compare(rdim, sh_rdim)
        shift_idx.append(sh_idx)
        shift_mask.append(sh_mask)
    return np.array(shift_idx).T, np.array(shift_mask).T,

def connected_components(coords, shifts):
    shift_idx, shift_mask = get_shift_intersections(coords, shifts)
    x, y = np.indices((len(shift_idx), len(shift_idx[0])))
    vertices = np.arange(len(coords))
    edges = np.array([x[shift_mask], shift_idx[shift_mask]]).T

    graph = igraph.Graph()
    graph.add_vertices(vertices)
    graph.add_edges(edges)
    graph_tags = graph.clusters().membership
    values = pd.DataFrame(graph_tags).groupby([0]).indices
    return values

coords = get_coords(arr)
shifts=((0,1),(1,0),(1,1),(-1,1))
comps = connected_components(coords, shifts=shifts)

for c in comps:
    print(coords[comps[c]].tolist()) 

Outcome

[[1, 2], [1, 3], [2, 1], [2, 4], [3, 0], [3, 1], [3, 4], [4, 2], [4, 3], [4, 4]]
[[1, 6], [2, 6], [3, 6], [4, 6], [5, 6], [6, 6]]

Explanation

Algorithm consists of these steps:

• We need to convert image to coordinates of non-white cells. It can be done using function:

  def get_coords(arr):
      x, y = np.indices(arr.shape)
      mask = arr != 255
      return np.array([y[mask], x[mask]]).T
  

  I'll name an outputting array by X for clarity. Here is an output of this array, visually:

• Next, we need to consider all the cells of each shift that intersects with X:

  In order to do that, we should solve a problem of intersections I posted few days before. I found it quite difficult to do using multidimensional numpy arrays. Thanks to Divakar, he proposes a nice way of dimensionality reduction using numexpr package which fastens operations even more than numpy. I implement it here in this function:

  def get_reduction(coords, s):
      d = {'s': s, 'c0': coords[:,0], 'c1': coords[:,1]}
      return ne.evaluate('c0*s+c1', d)
  

  In order to make it working, we should set a bound s which can be calculated automatically using a function

  def get_bounds(coords, increment):
      return np.max(coords[1]) + 1 + increment
  

  or inputted manually. Since algorithm requires increasing coordinates, pairs of coordinates might be out of bounds, therefore I have used a slight increment here. Finally, as a solution to my post I mentioned here, indexes of coordinates of X (reduced to 1D), that intersects with any other array of coordinates Y (also reduced to 1D) can be accessed via function

  def compare(r1, r2):
      # assuming r1 is a sorted array, returns:
      # 1) locations of r2 items in r1
      # 2) mask array of these locations
      idx = np.searchsorted(r1, r2)
      idx[idx == len(r1)] = 0
      mask = r1[idx] == r2
      return idx, mask
  

• Plugging all the corresponding arrays of shifts. As we can see, abovementioned function outputs two variables: an array of index locations in the main set X and its mask array. A proper indexes can be found using idx[mask] and since this procedure is being applied for each shift, I implemented get_shift_intersections(coords, shifts) method for this case.

• Final: constructing nodes & edges and taking output from igraph. The point here is that igraph performs well only with nodes that are consecutive integers starting from 0. That's why my script was designed to use mask-based access to item locations in X. I'll explain briefly how did I use igraph here:

  • I have calculated coordinate pairs:

      [[1, 2], [1, 3], [1, 6], [2, 1], [2, 4], [2, 6], [3, 0], [3, 1], [3, 4], [3, 6], [4, 2], [4, 3], [4, 4], [4, 6], [5, 6], [6, 6]]
    

  • Then I assigned integers for them:

      [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15]
    

  • My edges looks like this:

      [[0, 1], [1, 4], [2, 5], [3, 7], [3, 0], [4, 8], [5, 9], [6, 7], [6, 3], [7, 10], [8, 12], [9, 13], [10, 11], [11, 12], [11, 8], [13, 14], [14, 15]]
    

  • Output of graph.clusters().membership looks like this:

      [0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1]
    

  • And finally, I have used groupby method of Pandas to find indexes of separate groups (I use Pandas here because I found it to be the most efficient way of grouping in Python)

Notes

Download of igraph is not straightforward, you might need to install it from unofficial binaries.

Daile

So much work and OP hasn't even upvoted it. So you used intersection to get those subgraphs? – Kitchenmaid

Yes, I've been iterating through each shift of non-white cells and used intersection of initial cells with shifted cells as a masking operation. Resulting arrays are of the equal length and can be saved as a numpy matrix. – Daile