Finding the intersection of two circles

Question

I'm trying to find the intersections between two circles in Python(using Matplotlib) but can't get any values back.

I'm doing this by creating lists of X's and Y's for each individual circle(Matplotlib takes the first argument as X values and the second one as Y values when drawing a circle), and then intersecting the lists accordingly(e.g., circle1 x values with circle2 x values).

import numpy
import math
import matplotlib.pyplot as plt
import random

def origin_circle():
    global x_points
    global y_points
    global r
    global n
    r=1
    n=2**16
    x_points=[(r*math.cos(t)) for t in numpy.linspace(0, 2*numpy.pi*r, n+1)]
    y_points=[(r*math.sin(t)) for t in numpy.linspace(0, 2*numpy.pi*r, n+1)]

def new_circle(x_offset, y_offset):
    global x_points1
    global y_points1
    x_points1=[x_offset+(r*math.cos(t)) for t in numpy.linspace(0, 2*numpy.pi*r, n+1)]
    y_points1=[y_offset+(r*math.sin(t)) for t in numpy.linspace(0, 2*numpy.pi*r, n+1)]

origin_circle()
new_center= random.randint(0, len(x_points))
x_offset = x_points[new_center]
y_offset = y_points[new_center]
new_circle(x_offset, y_offset)
print(set(x_points1).intersection(set(x_points)))
print(set(y_points1).intersection(set(y_points)))

I expected to get values back, but the set that returned was empty.

Harbor

Each of your functions should return its x and y points if you want to be able to use that data outside of the function. docs.python.org/3/tutorial/controlflow.html#defining-functions – Menken

Since your cicles are composed by a finite number of points, are you sure that they have any points in common? They might have points in common only in the continuum limit. – Solitaire

There are formulas for computing the intersection (if any) of two circles given there centers and radii that don't involve enumerating any points on their circumference. – Copter

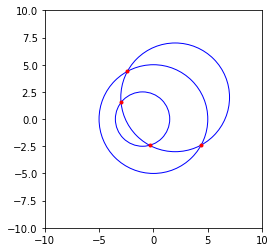
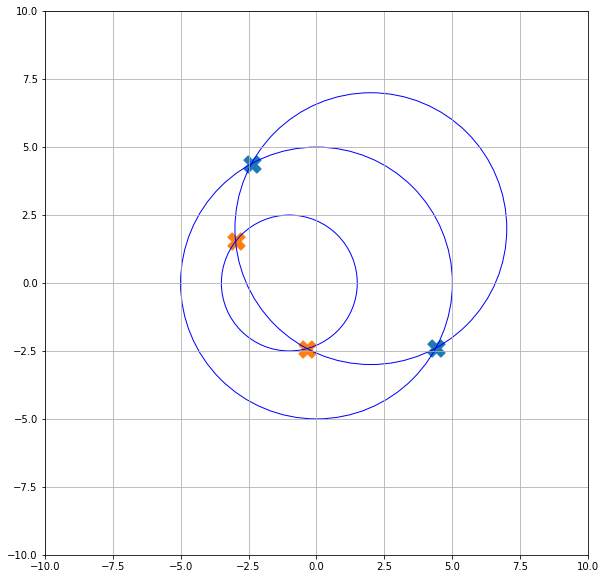
This line here (set(x_points1).intersection(set(x_points))) will practically never find an intersection between these two sets, just points that happen to exist in both sets. Since you are generating points around the outside of each circle it is extremely unlikely that two of these points will be exactly the same on different circles, even being off by 0.00000000001 will ensure that your intersection finds nothing. You'll need a better method for finding the intersection. – Mendel

Answer 1

The correct method to solve for intersection points of two circles is algebraically. You can't do it using points (x, y coordinates) because of infinite precision of coordinate system (real numbers).

If two circle intersect at two points then there is straight forward way to calculate those two points of intersection. The algebra is detailed here under section Intersection of two circles.

We can also eliminate the cases when two circles are not intersecting as below

• If distance between the two circle origins > sum of radius of two circle then it mean circle are separate and so not intersecting.
• If distance between the two circle origins < absolute difference between radius of two circle, then it mean one circle is contained with in other and so not intersecting.

Code to return the two intersecting points of two circle. Each cricle is describe by its center (x,y) and radius (r)

def get_intersections(x0, y0, r0, x1, y1, r1):
    # circle 1: (x0, y0), radius r0
    # circle 2: (x1, y1), radius r1

    d=math.sqrt((x1-x0)**2 + (y1-y0)**2)
    
    # non intersecting
    if d > r0 + r1 :
        return None
    # One circle within other
    if d < abs(r0-r1):
        return None
    # coincident circles
    if d == 0 and r0 == r1:
        return None
    else:
        a=(r0**2-r1**2+d**2)/(2*d)
        h=math.sqrt(r0**2-a**2)
        x2=x0+a*(x1-x0)/d   
        y2=y0+a*(y1-y0)/d   
        x3=x2+h*(y1-y0)/d     
        y3=y2-h*(x1-x0)/d 

        x4=x2-h*(y1-y0)/d
        y4=y2+h*(x1-x0)/d
        
        return (x3, y3, x4, y4)

Lets test it (visually) by plotting

# intersection circles
x0, y0 = 0, 0
r0 = 5
x1, y1 = 2, 2
r1 = 5

# intersecting with (x1, y1) but not with (x0, y0)
x2, y2 = -1,0
r2 = 2.5

circle1 = plt.Circle((x0, y0), r0, color='b', fill=False)
circle2 = plt.Circle((x1, y1), r1, color='b', fill=False)
circle3 = plt.Circle((x2, y2), r2, color='b', fill=False)

fig, ax = plt.subplots() 
ax.set_xlim((-10, 10))
ax.set_ylim((-10, 10))
ax.add_artist(circle1)
ax.add_artist(circle2)
ax.add_artist(circle3)

intersections = get_intersections(x0, y0, r0, x1, y1, r1)
if intersections is not None:
    i_x3, i_y3, i_x4, i_y4 = intersections 
    plt.plot([i_x3, i_x4], [i_y3, i_y4], '.', color='r')
    
intersections = get_intersections(x0, y0, r0, x2, y2, r2)
if intersections is not None:
    i_x3, i_y3, i_x4, i_y4 = intersections 
    plt.plot([i_x3, i_x4], [i_y3, i_y4], '.', color='r')

intersections = get_intersections(x1, y1, r1, x2, y2, r2)
if intersections is not None:
    i_x3, i_y3, i_x4, i_y4 = intersections 
    plt.plot([i_x3, i_x4], [i_y3, i_y4], '.', color='r')

plt.gca().set_aspect('equal', adjustable='box')

Output:

Plank

Answer 2

Take a look at what you generated:

new_center= random.randint(0, len(x_points))
x_offset = x_points[new_center]
y_offset = y_points[new_center]
new_circle(x_offset, y_offset)

# I'm sorting these for easier visualization
print(sorted(x_points))
print(sorted(x_points1))

Output:

[-1.0, -0.9807852804032304, -0.9807852804032304, -0.9238795325112868,
 -0.9238795325112867, -0.8314696123025455, -0.8314696123025453, -0.7071067811865477,
 -0.7071067811865475, -0.5555702330196022, -0.555570233019602, -0.38268343236509034,
 -0.3826834323650897, -0.19509032201612866, -0.1950903220161282,
 -1.8369701987210297e-16, 6.123233995736766e-17, 0.1950903220161283,
 0.19509032201612833, 0.38268343236508984, 0.38268343236509, 0.5555702330196018
, 0.5555702330196023, 0.7071067811865474, 0.7071067811865476, 0.8314696123025452,
 0.8314696123025452, 0.9238795325112865, 0.9238795325112867, 0.9807852804032303,
 0.9807852804032304, 1.0, 1.0]

[-2.0, -1.9807852804032304, -1.9807852804032304, -1.923879532511287,
 -1.9238795325112867, -1.8314696123025453, -1.8314696123025453, -1.7071067811865477,
 -1.7071067811865475, -1.5555702330196022, -1.555570233019602, -1.3826834323650903,
 -1.3826834323650896, -1.1950903220161286, -1.1950903220161282, -1.0000000000000002,
 -0.9999999999999999, -0.8049096779838717, -0.8049096779838717, -0.6173165676349102,
 -0.6173165676349099, -0.44442976698039816, -0.4444297669803977, -0.29289321881345265,
 -0.2928932188134524, -0.16853038769745476, -0.16853038769745476,
 -0.07612046748871348, -0.07612046748871326, -0.01921471959676968,
 -0.01921471959676957, 0.0, 0.0]

First of all, you have generated independent lists of coordinates; you do not have points as a coordinated pair of any kind.

Second, you did not list all of the points on the circle: you can't, since that's an infinite set. Instead, you generated a list (well, one each for x and y) of equally-spaced There is no mathematical reason to expect that you'll have an exact match between any two such coordinates, let alone happening to choose the two points on each circle that are exactly the points of intersection.

You get nothing back because your lists have no points in common. If you want to find the points of intersection, you'll need to do so by algebraic solution, or successive approximation, or some other method. For instance, take the difference of the two circles and solve that equation for y == 0.

Mellar

Answer 3

If you are working with circles, the proper approach to get the intersections is to use some algebra. There are four possible cases: no intersection, one intersection (tangency), two intersections, and infinite intersection (they are the same circle).Let us focus on the case of two intersections.

From https://math.stackexchange.com/a/256123/647423 what you can do is obtain a linear equation that relates x to y along the line that passes through the two points of intersection:

−2x(x1center−x2center)−2y(y1center−y2center) = (r1)^2−(r2)^2−((x1center)^2−(x2center)^2)−((y1center)^2−(y2center)^2).

From this you obtain a formula for y in terms of x, then substitute y into one of your circle formulas to obtain a quadratic for x. If you don't want to implement a quadratic equation solver, you can use numpy.roots like so:

root_array = np.roots(quadratic_coeff, linear_coeff, constant_coef)

Hephzibah

Answer 4

The above code of plotting the intersection points did not plot the intersecting points properly. I have adjusted the code to plot them as follows:

import matplotlib.pyplot as plt
import math

def get_intersections(x0, y0, r0, x1, y1, r1):
    # circle 1: (x0, y0), radius r0
    # circle 2: (x1, y1), radius r1

    d=math.sqrt((x1-x0)**2 + (y1-y0)**2)

    # non intersecting
    if d > r0 + r1 :
        return {}
    # One circle within other
    if d < abs(r0-r1):
        return {}
    # coincident circles
    if d == 0 and r0 == r1:
        return {}
    else:
        a=(r0**2-r1**2+d**2)/(2*d)
        h=math.sqrt(r0**2-a**2)
        x2=x0+a*(x1-x0)/d   
        y2=y0+a*(y1-y0)/d   
        x3=x2+h*(y1-y0)/d     
        y3=y2-h*(x1-x0)/d 
        x4=x2-h*(y1-y0)/d
        y4=y2+h*(x1-x0)/d
        return x3, y3, x4, y4

# intersection circles
x0, y0 = 0, 0
r0 = 5
x1, y1 = 2, 2
r1 = 5

# intersecting with (x1, y1) but not with (x0, y0)
x2, y2 = -1,0
r2 = 2.5

circle1 = plt.Circle((x0, y0), r0, color='b', fill=False)
circle2 = plt.Circle((x1, y1), r1, color='b', fill=False)
circle3 = plt.Circle((x2, y2), r2, color='b', fill=False)

fig = plt.figure(figsize = (10, 10)) 
plt.grid(True)
ax = fig.add_subplot(111)

ax.set_xlim((-10, 10))
ax.set_ylim((-10, 10))
ax.add_artist(circle1)
ax.add_artist(circle2)
ax.add_artist(circle3)

intersections1 = get_intersections(x0, y0, r0, x1, y1, r1)
print(intersections1)
if len(intersections1) > 0:
    print(intersections3)
    i_x3, i_y3, i_x4, i_y4 = intersections1 
    #plt.plot([i_x3, i_x4], [i_y3, i_y4], 'o', color='r')
    ax.scatter([i_x3, i_x4],[i_y3, i_y4] ,marker ='X',s=300,alpha=1)

intersections2 = get_intersections(x0, y0, r0, x2, y2, r2)
print(intersections2)
if len(intersections2) > 0:
    i_x3, i_y3, i_x4, i_y4 = intersections2 
    plt.plot([i_x3, i_x4], [i_y3, i_y4], 'o', color='r')
    ax.scatter([i_x3, i_x4],[i_y3, i_y4] ,marker ='X',s=300,alpha=1)

intersections3 = get_intersections(x1, y1, r1, x2, y2, r2)

if len(intersections3) > 0:
    print(intersections3)
    i_x3, i_y3, i_x4, i_y4 = intersections3 
    #plt.plot([i_x3, i_x4], [i_y3, i_y4], 'o', color='r')
    ax.scatter([i_x3, i_x4],[i_y3, i_y4] ,marker ='X',s=300,alpha=1)
plt.gca().set_aspect('equal', adjustable='box')

The output is given in the image:

Peacock

Answer 5

Wrong language for math/geometry things. This is what it looks like in a more appropriate language (WL)

 Circle @@@ Thread @ {RandomReal[{-1,1},{3,2}], RandomReal[{.5,1},3]} // 
 Graphics[{
    #, Red, 
    RegionIntersection @@@ #~Subsets~{2}
 }]&

Cosignatory