I've implemented a SAH kd-tree based upon the paper On building fast kd-Trees for Ray Tracing, and on doing that in O(N log N) by Wald and Havran. Note I haven't done their splicing and merging suggestion right at the end to speed up the building of the tree, just the SAH part.
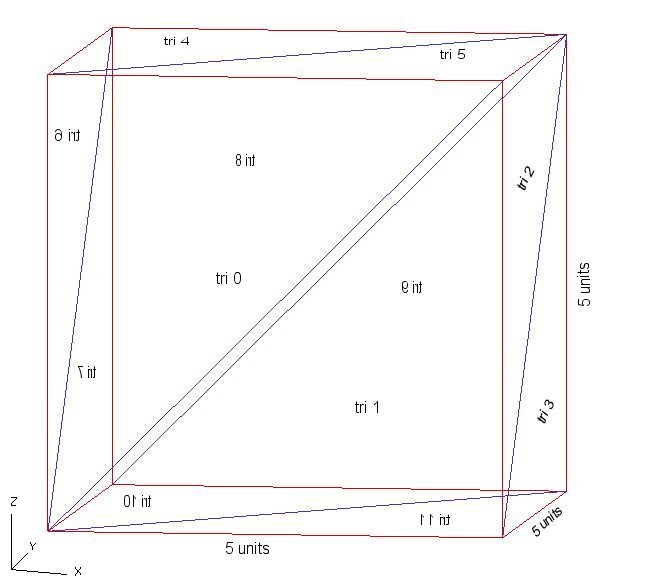
I'm testing the algorithm with an axis-aligned cube where each face is split into two triangles, so I have N = 12 triangles in total. The bottom-left vertex (i.e. the one nearest the axes) is actually at the origin.
Face Triangle
----------------
Front: 0, 1
Left: 6, 7
Right: 2, 3
Top: 4, 5
Bottom: 10, 11
Back: 8, 9
Assuming node traversal cost Ct = 1.0 and intersection cost Ci = 10.0. We first find the cost of not splitting which is Cns = N * Ci = 12 * 10.0 = 120.0.
Now we go through each axis in turn and do an incremental sweep through the candidate split planes to see if the cost of splitting is cheaper. The first split plane is p = <x,0>. We have Nl = 0, Np = 2 and Nr = 10 (that is, the number of triangles on the left, in the plane, and to the right of the plane). The two triangles in the plane are number 6 and 7 (the left face). All others are to the right.
The SAH(p,V,Nl,Nr,Np) function is now executed. This takes the split plane, the voxel V to be split, and the numbers of left/right/plane triangles. It computes the probability of hitting the left (flat) voxel as Pl = SA(Vl)/SA(V) = 50/150 = 1/3, the right probability as Pr = SA(Vr)/SA(V) = 150/150 = 1. Now it runs the cost function twice; first with the planar triangles on the left, then with the planar triangles on the right to get Cl and Cr respectively.
The cost function C(Pl,Pr,Nl,Nr) returns bias * (Ct + Ci(Pl * Nl + Pr * Nr))
Cl: cost with planar triangles on the left (Nl = 2, Nr = 10)
bias = 1 we aren't biasing as neither left nor right voxel is empty.
Cl = 1 * (1 + 10(1/3 * 2 + 1 * 10)) = 107.666
Cr: cost with planar triangles on the right (Nl = 0, Nr = 12)
bias = 0.8 empty cell bias comes into play.
Cr = 0.8 * (1 + 10(1/3 * 0 + 1 * 12)) = 96.8
The algorithm determines that Cr = 96.8 is better than splitting the two triangles off into a flat cell Cl = 107.666 and also better than not splitting the voxel at all Cns = 120.0. No other candidate splits are found to be cheaper. We therefore split into an empty left child, and a right child containing all the triangles. When we recurse into the right child to continue the tree building, we perform exactly the same steps as above. It's only because of a max depth termination criterion that this doesn't cause a stack overflow. The resultant tree is very deep.
The paper claims to have thought about this sort of thing:
During clipping, special care has to be taken to correctly handle special cases like “flat” (i.e., zero-volume) cells, or cases where numerical inaccuracies may occur (e.g., for cells that are very thin compared to the size of the triangle). For example, we must make sure not to “clip away” triangles lying in a flat cell. Note that such cases are not rare exceptions, but are in fact encouraged by the SAH, as they often produce minimal expected cost.
This local approximation can easily get stuck in a local minimum: As the local greedy SAH overestimates CV (p), it might stop subdivision even if the correct cost would have indicated further subdivision. In particular, the local approximation can lead to premature termination for voxels that require splitting off flat cells on the sides: many scenes (in particular, architectural ones) contain geometry in the form of axis-aligned boxes (a light fixture, a table leg or table top, . . . ), in which case the sides have to be “shaved off” until the empty interior is exposed. For wrongly chosen parameters, or when using cost functions different from the ones we use (in particular, ones in which a constant cost is added to the leaf estimate), the recursion can terminated prematurely. Though this pre-mature exit could also be avoided in a hardcoded way—e.g., only performing the automatic termination test for non-flat cells—we propose to follow our formulas, in which case no premature exit will happen.
Am I doing anything wrong? How can I correct this?