Matching similar eigenspectra in two matrices

Question

I have two matrices for which part of the eigenspectrum of one matrix, very closely resembles the eigenspectrum of another matrix, but the only way I'm (currently) able to verify this is quite inelegant.

I am open to any solution, but to present examples here of what I seek, I find it easiest to use MATLAB syntax: In the first example I will define matrices A and B such that two eigenvalues of B are also found in A, and the corresponding two eigenvectors of B are also eigenvectors of A with the same eigenvalues, but this is not apparent without taking the eigenvectors of B whose eigenvalues are shared with A and "searching" to see if those same eigenvectors have the same eigenvalues in A.

Here's an example of two such matrices A and B:

  A      = diag([1 1 -1 -1 -1 -1 1 1 -1 -1 1 1 1 1 -1 -1]);
  B      = diag([19.9385 7.6177 17.2969 9.6177 11.3208 -1 8.6792 1 11.3208 -1 8.6792 1 19.9385 7.6177 17.2969 9.6177]); 
  B(2,1) = 9.2832; B(4,3)=B(2,1); B(14,13)=-B(2,1); B(16,15)=-B(2,1); 
  B      = tril(B,-1)'+B; % Make it Hermitian by mirroring the lower triangle into the upper triangle

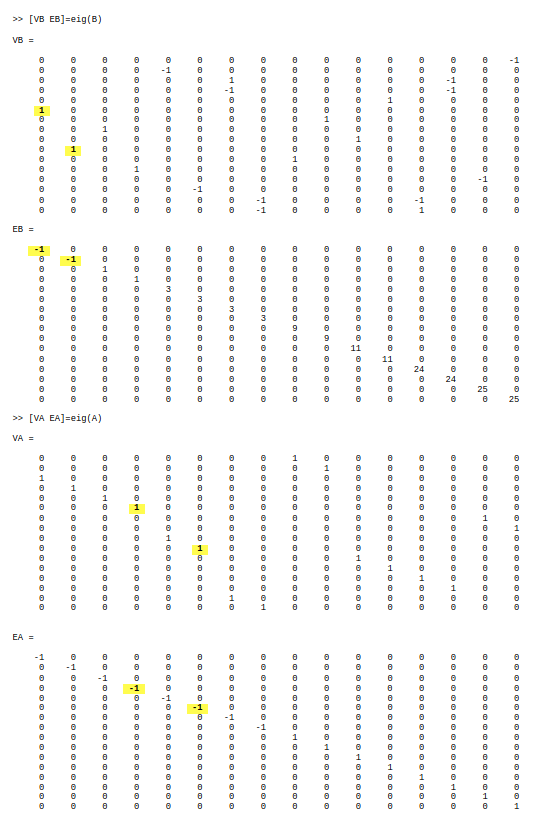
By running the command [eig(A)' ; eig(B)'] we see that two of A's eigenvalues (both of them being -1) are shared with B's eigenvalues (A in the top row and B in the bottom row):

-1 -1 -1 -1 -1 -1 -1 -1  1  1  1  1  1  1  1  1
-1 -1  1  1  8  8  9  9 10 10 11 11 17 17 20 20

The eigenvectors of A with eigenvalues -1 also match eigenvectors of B with eigenvalues of -1 but while these appear in columns 1 and 2 of the eigenvector matrix VA of A, they appear in columns 4 and 6 of eigenvector matrix VB of B:

Is there a more elegant way to see this without brute force searching to see if the eigenvectors of the common eigenvalues are shared?

Here is slightly more complicated example where the matrix sizes are not the same, and the eigenvectors are no longer exactly the same, but they are still equivalent (multiplying an eigenvector by a scalar results in a vector that is also an eigenvector, with the same eigenvalue):

I have done quite a bit of searching for a solution, and can say that I'm aware of some related tools such as:

• MATLAB's sort command, but unfortunately this won't work for sorting the above eigenvectors
• Simultaneous diagonalization of two matrices, which sounds quite relevant but seems not to be helpful for this goal.
• Another "simultaneous diagonalization" question was asked on Mathematics.SE but received no answers (though a useful command for extracting eigenvectors corresponding to an eigenvalue of k in the comments: V(:,diag(D)==k)).
• Matrices must commute to share an eigenvector, but this only tells me when not to both trying to match eigenvectors, and doesn't bring me closer to my goal of being able to elegantly match eigenvectors.

Jepum

There's an even more complicated possibility: if you have degenerate eigenvalues then the corresponding eigenvectors lie in a multidimensional space, and you can in principle and up with arbitrary two orthogonal eigenvectors (arbitrary for each matrix, or even each eigendecomposition if the algorithm uses randomness). For a non-degenerate eigenvalue you could take the complex outer product of the eigenvector with itself (|v><v| dyadic product) which would remove the phase ambiguity. It's too late for me to try to figure out if something like this works for the degenerate case. – Ephrem

Answer 1

I will first compare all the eigenvalues and all the eigenvectors and then see if both eigenvalues and eigenvectors matches at the same time.

I am not sure if this approach is more elegant. This could be even more brute force. But you can get rid of the tidious searching and matching eigenvalue-eigenvector process and this code should be shorter.

The eigenvectors are compared by taking inner products, as they are easier to implement than outer products. Since matlab normalizes the eigenvectors automatically, by Cauchy–Schwarz inequality, the inner product of linear dependent eigenvectors should be either -1 or 1.

% compare eigenvalues
is_val_same = abs(diag(EA)-diag(EB).') < 1e-8;

% total number of eigenvectors
m=size(VA,2);
n=size(VB,2);

% calculate dot products
dotAB = sum(permute(repmat(conj(VB), 1, 1, m), [1 3 2]).*repmat(VA, 1, 1, n), 1);
dotAB = reshape(dotAB, m, n);

% compare eigenvectors
is_vec_same = abs(abs(dotAB)-1) < 1e-8;

% find the matching eigen pairs
[index_A, index_B]=find(is_vec_same & is_val_same)

Output:

index_A =
 4
 6
16
12

index_B =
 1
 2
 3
 4

This means columns 4 6 16 12 of A correspond to columns 1 2 3 4 of B, respectively.

It also works when matrix sizes are not the same. Dengeneracy can be identified by looking for repeated eigenvectors of A and B, using code similar to that above.

Rathskeller