How to use OpenCV triangulatePoints

Question

I'm struggling to get the OpenCV triangulatePoints function to work. I'm using the function with point matches generated from optical flow. I'm using two consecutive frames/positions from a single moving camera.

Currently these are my steps:

The intrinsics are given and look like one would expect:

2.6551e+003  0.           1.0379e+003
0.           2.6608e+003  5.5033e+002
0.           0.           1.

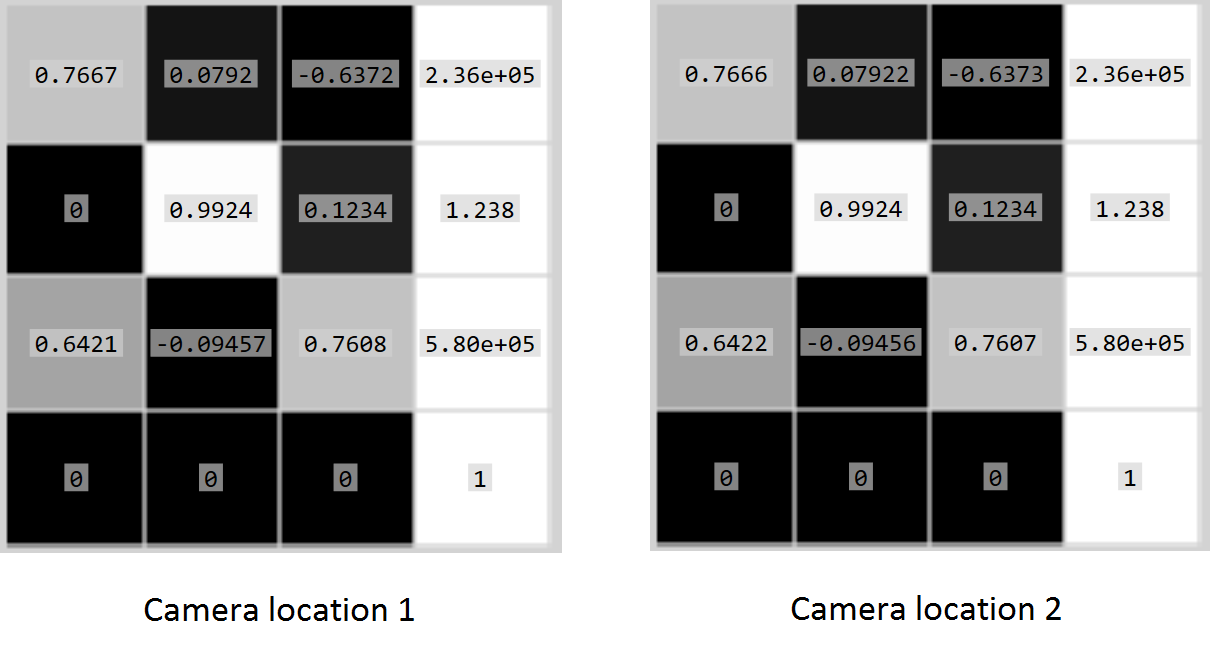
I then compute the two extrinsic matrices ([R|t]) based on (highly accurate) GPS and camera position relative to the GPS. Note that the GPS data uses a cartesian coordinate system around The Netherlands which uses meters as units (so no weird lat/lng math is required). This yields the following matrices:

Next, I simply remove the bottom row of these matrices and multiply them with the intrinsic matrices to get the projection matrices:

projectionMat = intrinsics * extrinsics;

This results in:

My image points simply consist of all the pixel coordinates for the first set,

(0, 0)...(1080, 1920)

and all pixel coordinates + their computed optical flow for the second set.

(0 + flowY0, 0 + flowX0)...(1080 + flowYN, 1920 + flowXN)

To compute the 3D points, I feed the image points (in the format OpenCV expects) and projection matrices to the triangulatePoints function:

cv::triangulatePoints(projectionMat1, projectionMat2, imagePoints1, imagePoints2, outputPoints);

Finally, I convert the outputPoints from homogeneous coordinates by dividing them by their fourth coordinate (w) and removing this coordinate.

What I end up with is some weird cone-shaped point cloud:

Now I've tried every combination of tweaks I could think of (inverting matrices, changing X/Y/Z order, inverting X/Y/Z axes, changing multiplication order...), but everything yields similarly strange results. The one thing that did give me better results was simply multiplying the optical flow values by 0.01. This results in the following point cloud:

This is still not perfect (areas far away from the camera look really curved), but much more like I would expect.

I'm wondering if anybody can spot something I'm doing wrong. Do my matrices look ok? Is the output I'm getting related to a certain problem?

What I'm quite certain of, is that it's not related to the GPS or optical flow, since I've tested multiple frames and they all yield the same type of output. I really think it has to do with the triangulation itself.

Trangtranquada

Hey, so are you trying to replicate a Structure-from-Motion? The coordinates that you refer (X,Y,Z), are in the GPS coordinate system? This may not be the best source but here you have the complete pipeline of a SFM implementation with opencv. Unfortunately, the book which explains this step by step is paid. – Afternoon

@Afternoon Thanks! That's the one I found too, but I haven't quite figured out the difference between that source and my code, as it's structured quite differently, so finding out which matrix is which etc. is difficult. – Trangtranquada

Well, I'm not sure what is wrong with your code, but I believe that you should start by using local coordinates instead of the GPS (lat, lon, alt is a spherical system and may lead to weird artifacts on Y axis (in your case) when using SFM. In example, looking at your camera translation matrix (t) you have large values (order of e+05) for X and Z and small values for Y (1.238) which means you will have large variations horizontal axis and small vertically. Hence that weird shaped point cloud. Did not test, just a suggestion. – Afternoon

@Afternoon All very valid points, although I should've added information about the GPS system. All lat/lng coordinates were converted to the Dutch "Rijksdriehoek" system, which is a cartesian coordinate system that encopasses The Netherlands. For this reason, the X and Z values are large, since they are in meters and are somewhere in the middle of The Netherlands. The Y value represents the height at which the camera is mounted (1.238m). I'll edit this into the question. – Trangtranquada

Alright, so, in this statement "Finally, I convert the outputPoints from homogeneous coordinates by multiplying them by their fourth coordinate (w) and removing this coordinate.". You mean, by dividing them right? – Afternoon

same problem here, used all the conventions and things like in this example : tobias-weis.de/… – Foeticide

Answer 1

triangulatePoints() is for stereo camera , not for monocular camera!

In the opencv doc, I read the following express :

The function reconstructs 3-dimensional points (in homogeneous coordinates) by using their observations with a stereo camera. Projections matrices can be obtained from stereoRectify()

Wonted

Answer 2

In my case I had to fix the convention used in the rotation matrices in order to calculate the projection matrix, please make sure you are using this convention for both cameras :

rotationMatrix0 = rotation_by_Y_Matrix_Camera_Calibration(camera_roll)*rotation_by_X_Matrix_Camera_Calibration(camera_pitch)  *rotation_by_Z_Matrix_Camera_Calibration(camera_yaw);



Mat3x3 Algebra::rotation_by_Y_Matrix_Camera_Calibration(double yaw)
{
    Mat3x3 matrix;
    matrix[2][2] = 1.0f;

    double sinA = sin(yaw), cosA = cos(yaw);
    matrix[0][0] = +cosA; matrix[0][1] = -sinA;
    matrix[1][0] = +sinA; matrix[1][1] = +cosA;



    return matrix;
}

Mat3x3 Algebra::rotation_by_X_Matrix_Camera_Calibration(double pitch)
{

    Mat3x3 matrix;
    matrix[1][1] = 1.0f;

    double sinA = sin(pitch), cosA = cos(pitch);

    matrix[0][0] = +cosA; matrix[0][2] = +sinA;
    matrix[2][0] = -sinA; matrix[2][2] = +cosA;


    return matrix;
}

Mat3x3 Algebra::rotation_by_Z_Matrix_Camera_Calibration(double roll)
{

    Mat3x3 matrix;
    matrix[0][0] = 1.0f;

    double sinA = sin(roll), cosA = cos(roll);
    matrix[1][1] = +cosA; matrix[1][2] = -sinA;
    matrix[2][1] = +sinA; matrix[2][2] = +cosA;



    return matrix;
}

Foeticide