pymc3 multivariate traceplot color coding

Question

I am new to working with pymc3 and I am having trouble generating an easy-to-read traceplot. I'm fitting a mixture of 4 multivariate gaussians to some (x, y) points in a dataset. The model runs fine. My question is with regard to manipulating the pm.traceplot() command to make the output more user-friendly. Here's my code:

import matplotlib.pyplot as plt
import numpy as np
model = pm.Model()
N_CLUSTERS = 4
with model:
    #cluster prior
    w = pm.Dirichlet('w', np.ones(N_CLUSTERS))
    #latent cluster of each observation
    category = pm.Categorical('category', p=w, shape=len(points))

    #make sure each cluster has some values:
    w_min_potential = pm.Potential('w_min_potential', tt.switch(tt.min(w) < 0.1, -np.inf, 0))
    #multivariate normal means
    mu = pm.MvNormal('mu', [0,0], cov=[[1,0],[0,1]], shape = (N_CLUSTERS,2) )
    #break symmetry
    pm.Potential('order_mu_potential', tt.switch(
                                                tt.all(
                                                   [mu[i, 0] < mu[i+1, 0] for i in range(N_CLUSTERS - 1)]), -np.inf, 0))
    #multivariate centers
    data = pm.MvNormal('data', mu =mu[category], cov=[[1,0],[0,1]],  observed=points)

 with model:
     trace = pm.sample(1000)

A call to pm.traceplot(trace, ['w', 'mu']) produces this image:

As you can see, it is ambiguous which mean peak corresponds to an x or y value, and which ones are paired together. I have managed a workaround as follows:

from cycler import cycler
#plot the x-means and y-means of our data!
fig, (ax0, ax1) = plt.subplots(nrows=2)
plt.xlabel('$\mu$')
plt.ylabel('frequency')
for i in range(4):
    ax0.hist(trace['mu'][:,i,0], bins=100, label='x{}'.format(i), alpha=0.6);
    ax1.hist(trace['mu'][:,i,1],bins=100, label='y{}'.format(i), alpha=0.6);
ax0.set_prop_cycle(cycler('color', ['c', 'm', 'y', 'k']))
ax1.set_prop_cycle(cycler('color', ['c', 'm', 'y', 'k']))
ax0.legend()
ax1.legend()

This produces the following, much more legible plot:

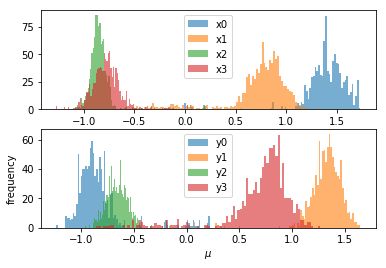
I have looked through the pymc3 documentation and recent questions here, but to no avail. My question is this: is it possible to do what I have done here with matplotlib via builtin methods in pymc3, and if so, how?

Used

Answer 1

Better differentiation between multidimensional variables and the different chains was recently added to ArviZ (the library PyMC3 relies on for plotting).

In ArviZ latest version, you should be able to do:

az.plot_trace(trace, compact=True, legend=True)

to get the different dimensions of each variable distinguished by color and the different chains distinguished by linestyle. The default setting is using matplotlib's default color cycle and 4 different linestyles, solid, dashed, dotted and dash-dotted. Both properties can be set to custom aesthetics and custom values by using compact_prop to customize dimension representation and chain_prop to customize chain representation. In addition, if using compact, it may also be a good idea to use combined=True to reduce the clutter in the first column. As an example:

az.plot_trace(trace, compact=True, combined=True, legend=True, chain_prop=("ls", "-"))

would plot the KDEs in the first column using the data from all chains, and would plot all chains using a solid linestyle (due to combined arg, only relevant for the second column). Two legends will be shown, one for the chain info and another for the compact info.

Hooten

Answer 2

At least in recent versions, you can use compact=True as in:

pm.traceplot(trace, var_names = ['parameters'], compact=True)

to get one graph with all you params combined Docs in: https://arviz-devs.github.io/arviz/_modules/arviz/plots/traceplot.html

However, I haven't been able to get the colors to differ between lines

Inenarrable

You can get different colors by setting compact=False – Vegetative