I'm not sure what follows is what you want - I'm fairly sure it's not what you had in mind - but if it sounds reasonable you might try it out.
Because the distance is simply at most d, and can be anything less than that, it seems at first blush like a greedy algorithm should work here. Always place the next line(s) so that (1) as few as possible are needed and (2) they are as far away from existing lines as possible.
Assume you have an optimal algorithm for this problem, and it places the next line(s) at distance a <= d from the last line. Say it places b lines. Our greedy algorithm will definitely place no more than b lines (since the first criterion is to place as few as possible), and if it places b lines it will place them at distance c with a <= c <= d, since it then places the lines as far as possible.
If the greedy algorithm did not do what the optimal algorithm did, it differed in one of the following ways:
It placed the same or fewer lines farther away. Suppose the optimal algorithm had gone on to place b' lines at distance a' away at the next step. Then these lines would be at distance a+a' and there would be b+b' lines in total. But the greedy algorithm can mimic the optimal algorithm in this case by placing b' lines at displacement a+a' by choosing c' = (a+a') - c. Since c > a and a' < d, c' < d and this is a legal placement.
It placed fewer lines closer together. This case is actually problematic. It is possible that this places k unnecessary lines, if any placement requires at least k lines and the farthest ones require more, and the arrangement of holes is chosen so that (e.g.) the distance it spans is a multiple of d.
So the greedy algorithm turns out not to work in case 2. However, it does in other cases. In particular, our observation in the first case is very useful: for any two placements (distance, lines) and (distance', lines'), if distance >= distance' and lines <= lines', the first placement is always to be preferred. This suggests the following algorithm:
PlaceLines(start, stop)
// if we are close enough to the other edge,
// don't place any more lines.
if start + d >= stop then return ([], 0)
// see how many lines we can place at distance
// d from the last placed lines. no need to
// ever place more lines than this
nmax = min_lines_at_distance(start + d)
// see how that selection pans out by recursively
// seeing how line placement works after choosing
// nmax lines at distance d from the last lines.
optimal = PlaceLines(start + d, stop)
optimal[0] = [d] . optimal[0]
optimal[1] = nmax + optimal[1]
// we only need to try fewer lines, never more
for n = 1 to nmax do
// find the max displacement a from the last placed
// lines where we can place n lines.
a = max_distance_for_lines(start, stop, n)
if a is undefined then continue
// see how that choice pans out by placing
// the rest of the lines
candidate = PlaceLines(start + a, stop)
candidate[0] = [a] . candidate[0]
candidate[1] = n + candidate[1]
// replace the last best placement with the
// one we just tried, if it turned out to be
// better than the last
if candidate[1] < optimal[1] then
optimal = candidate
// return the best placement we found
return optimal
This can be improved by memoization by putting results (seq, lines) into a cache indexed by (start, stop). That way, we can recognize when we are trying to compute assignments that may already have been evaluated. I would expect that we'd have this case a lot, regardless of whether you use a coarse or a fine discretization for problem instances.
I don't get into details about how max_lines_at_distance and max_distance_for_lines functions might work, but maybe a word on these.
The first tells you at a given displacement how many lines are required to span the geometry. If you have pixelated your geometry and colored holes black, this would mean looking at the row of cells at the indicated displacement, considering the contiguous black line segments, and determining from there how many lines that implies.
The second tells you, for a given candidate number of lines, the maximum distance from the current position at which that number of lines can be placed. You could make this better by having it tell you the maximum distance at which that number of lines, or fewer, could be placed. If you use this improvement, you could reverse the direction in which you're iterating n and:
- if
f(start, stop, x) = a and y < x, you only need to search up to a, not stop, from then on;
- if
f(start, stop, x) is undefined and y < x, you don't need to search any more.
Note that this function can be undefined if it is impossible to place n or fewer lines anywhere between start and stop.
Note also that you can memorize separately for these functions to save repeated lookups. You can precompute max_lines_at_distance for each row and store it in a cache for later. Then, max_distance_for_lines could be a loop that checks the cache back to front inside two bounds.

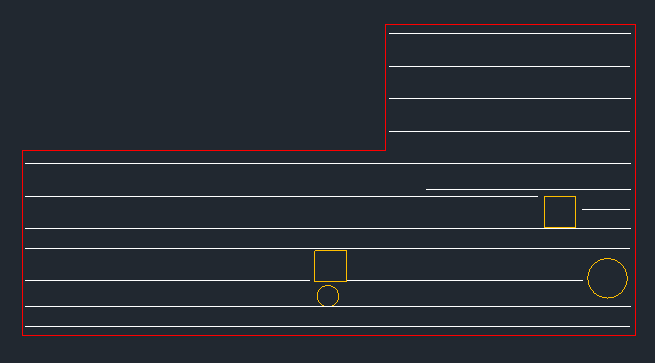
y mod I == 0for each line, where y is the line's Y coordinate. You are right that I am missing a constraint here, so I added a 4th one: Each available point inside the shape cannot be further from a line thanD/2. I edited the main question. The goal is that if a line collides with a hole, we want to put it next to the hole and keep its full length instead of having it cut in the middle. Hence the objective of minimizingNinstead of minimizing the total length of the lines. – Pharmaceutics