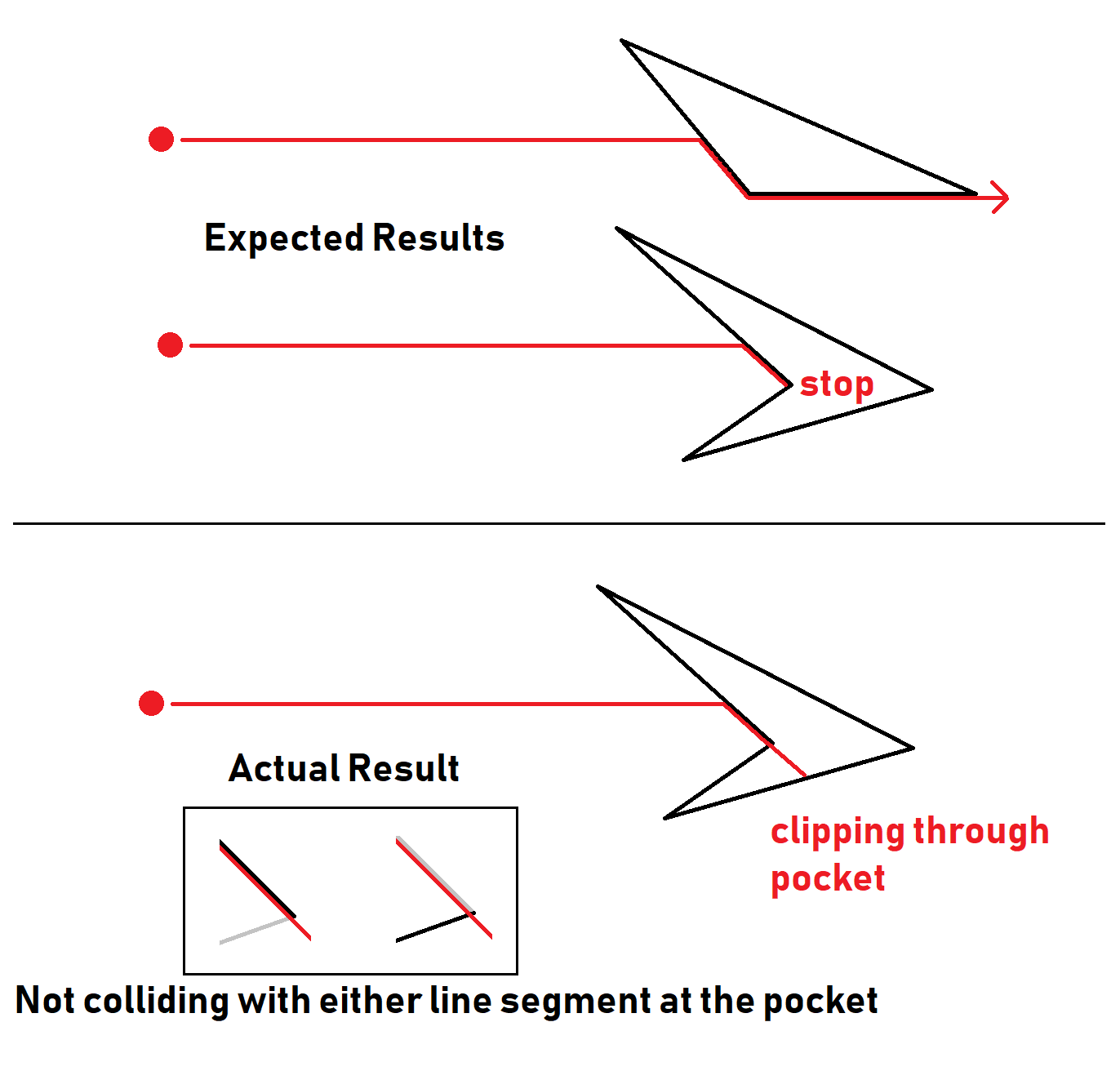
I'm trying to write a function to handle movement within a game I'm programming. What I have nearly works, but there are a couple situations where it breaks down.
I've coded up a minimal demonstrative example, presented below. In this example, I'm trying to calculate the travel of an object, represented by a point, and movement vector. This object's movement path is checked against a collection of polygons, which are broken down into line segments for testing. When this object collides with a line segment, I want it to slide along that segment (rather than stop or bounce away).
To do this, I check along my intended path for collisions, and if I find an intersection, I do a new test from that intersection point along the path of the line segment I've collided with, with the magnitude of the remainder of movement.
The problem arises when we slide along a line segment into a "pocket". Often times, the collision check will pass on both of the line segments that form the pocket, and the object will slip through. Because I'm travelling parallel to one of the line segments, and I'm intersecting with both line segments at an end points, I believe this issue is caused by floating point error. Whether or not it slips through, is caught, or is caught once and then slips through on the second check seems to be totally random.
I'm calculating intersection using a simple algorithm I found here: https://mcmap.net/q/122342/-how-do-i-compute-the-intersection-point-of-two-lines, but I've tried many other algorithms as well. All exhibit the same problems.
(Vector2 is class provided by the Unity library, it just holds x and y coordinates as floats. The Vector2.Dot function just calculates the dot product).
//returns the final destination of the intended movement, given the starting position, intended direction of movement, and provided collection of line segments
//slideMax provides a hard cap on number of slides allowed before we give up
Vector2 Move(Vector2 pos, Vector2[] lineStarts, Vector2[] lineEnds, Vector2 moveDir, int slideMax)
{
int slideCount = 0;
while (moveDir != Vector2.zero && slideCount < slideMax)
{
pos = DynamicMove(pos, lineStarts, lineEnds, moveDir, out moveDir);
slideCount++;
}
return pos;
}
//returns what portion of the intended movement can be performed before collision, and the vector of "slide" that the object should follow, if there is a collision
Vector2 DynamicMove(Vector2 pos, Vector2[] lineStarts, Vector2[] lineEnds, Vector2 moveDir, out Vector2 slideDir)
{
slideDir = Vector2.zero;
float moveRemainder = 1f;
for (int i = 0; i < lineStarts.Length; i++)
{
Vector2 tSlide;
float rem = LineProj(pos, moveDir, lineStarts[i], lineEnds[i], out tSlide);
if (rem < moveRemainder)
{
moveRemainder = rem;
slideDir = tSlide;
}
}
return pos + moveDir * moveRemainder;
}
//Calculates point of collision between the intended movement and the passed in line segment, also calculate vector of slide, if applicable
float LineProj(Vector2 pos, Vector2 moveDir, Vector2 lineStart, Vector2 lineEnd, out Vector2 slideDir)
{
slideDir = new Vector2(0, 0);
float start = (lineStart.x - pos.x) * moveDir.y - (lineStart.y - pos.y) * moveDir.x;
float end = (lineEnd.x - pos.x) * moveDir.y - (lineEnd.y - pos.y) * moveDir.x;
if (start < 0 || end > 0)
return 1;
//https://mcmap.net/q/122342/-how-do-i-compute-the-intersection-point-of-two-lines
//Uses Cramer's Rule
float L1A = -moveDir.y;
float L1B = moveDir.x;
float L1C = -(pos.x *(moveDir.y + pos.y) - (moveDir.x + pos.x)*pos.y);
float L2A = lineStart.y - lineEnd.y;
float L2B = lineEnd.x - lineStart.x;
float L2C = -(lineStart.x * lineEnd.y - lineEnd.x * lineStart.y);
float D = L1A * L2B - L1B * L2A;
float Dx = L1C * L2B - L1B * L2C;
float Dy = L1A * L2C - L1C * L2A;
if (D == 0)
return 1;
Vector2 inter = new Vector2(Dx / D, Dy / D);
if (Vector2.Dot(inter - pos, moveDir) < 0)
return 1;
float t = (inter - pos).magnitude / moveDir.magnitude;
if (t > 1)
return 1;
slideDir = (1 - t) * Vector2.Dot((lineEnd - lineStart).normalized, moveDir.normalized) * (lineEnd - lineStart).normalized;
return t;
}
Is there some way to calculate collision that isn't susceptible to this sort of problem? I imagine I can't totally eradicate floating point error, but is there a way to check that will at least guarantee I collide with ONE of the two line segments at the pocket? Or is there something more fundamentally wrong with going about things in this way?
If anything is unclear I can draw diagrams or write up examples.
EDIT: Having reflected on this issue more, and in response to Eric's answer, I'm wondering if converting my math from floating point to fixed point could solve the issue? In practice I'd really just be converting my values (which can fit comfortably in the range of -100 to 100) to ints, and then performing the math under those constraints? I haven't pieced all the issues together quite yet, but I might give that a try. If anyone has any information about anything like that, I'd be appreciative.