This can be seen as a generalization of the tree diameter problem, because the largest of those lengths equals the diameter of the tree. The height of a tree for every node as root is easily found in O(n2) time by running a known algorithm from that node. You can look up how to find the height of a tree with given root, I'm not going to discuss it here. I'll explain how to do it in O(n) time using 2 DFS.
Since it is a tree, every node has one parent, which is the node 'p' from where the node 'u' was discovered during DFS. Similarly, the nodes discovered from 'u' are considered its children.
We run two DFS. The first one calculates the height of the tree rooted at 'u' considering its children. The second DFS calculates the length of the longest path starting at 'u' through its parent 'p'. This makes sense if you imagine the tree being rooted at 'u', when 'p' becomes one of its children. The maximum of these two values is the height of the tree rooted at node 'u' a.k.a. the maximum length of a path that begins at node 'u'. The sum of these two values is the diameter of the tree rooted at node 'u'.
However, your question includes another part which is to print only unique paths. In other words, exclude the paths that are contained in another. That is a whole different algorithm question, and I leave it to you with a hint. The idea is that every path that is included in a larger path is the prefix of some suffix of the larger path.
I give a Python implementation below for calculating the heights, explanation inline with the code.
def all_longest_paths(n: int, edges: list[list[int]]) -> list[int]:
g: dict[int, list[int]] = defaultdict(list)
for u, v in edges:
g[u].append(v)
g[v].append(u)
heights = [[-1, -1] for _ in range(n)]
_calculate_height(g, heights, 0, -1)
longest_paths_up = [0] * n
_calculate_longest_path_up(g, heights, longest_paths_up, 0, -1)
# Sum for diameter.
return [max(heights[i][0], longest_paths_up[i]) for i in range(n)]
def _calculate_height(g: dict[int, list[int]], heights: list[list[int]], u: int, p: int) -> None:
"""
Calculates the height of the tree rooted at node u and sets the value at heights[u].
Actually, it calculates the top 2 heights such that heights[u][0] >= heights[u][1].
If u is a leaf, heights = [0, 0]. If u has only one child, then, heights[u][1] = 0.
:param g: graph as adjacency list
:param heights: the heights array, it is updated in place
:param u: the root node
:param p: the parent node of u
:return: nothing
"""
for v in filter(lambda x: x != p, g.get(u, [])):
_calculate_height(g, heights, v, u)
ht_v = heights[v][0]
if ht_v > heights[u][0]:
heights[u][1], heights[u][0] = heights[u][0], ht_v
elif ht_v > heights[u][1]:
heights[u][1] = ht_v
heights[u][0] += 1
heights[u][1] += 1
def _calculate_longest_path_up(
g: dict[int, list[int]], heights: list[list[int]], lp_up: list[int], u: int, p: int
) -> None:
"""
Calculates the length of the longest path of the tree rooted at node u through its
parent p and sets the value at lp_up[u].
:param g: graph as adjacency list
:param heights: the heights array
:param lp_up: the longest paths through p array, it is updated in place
:param u: the root node
:param p: the parent node of u
:return: nothing
"""
for v in filter(lambda x: x != p, g.get(u, [])):
# If the longest path starting at u goes through v,
# then we use another path that goes through a
# sibling of v.
if heights[u][0] == heights[v][0] + 1:
ht = heights[u][1]
else:
# The longest path starting at u doesn't go
# through v, so, use that value.
ht = heights[u][0]
# The longest path starting at v may go through
# one of its siblings x (v-u-x-...), or it may
# not (v-u-p-...).
lp_up[v] = max(ht, lp_up[u]) + 1
_calculate_longest_path_up(g, heights, lp_up, v, u)
If you prefer visual aid, there's a YouTube video also, although I found it somewhat long and rambling.

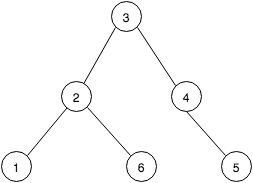
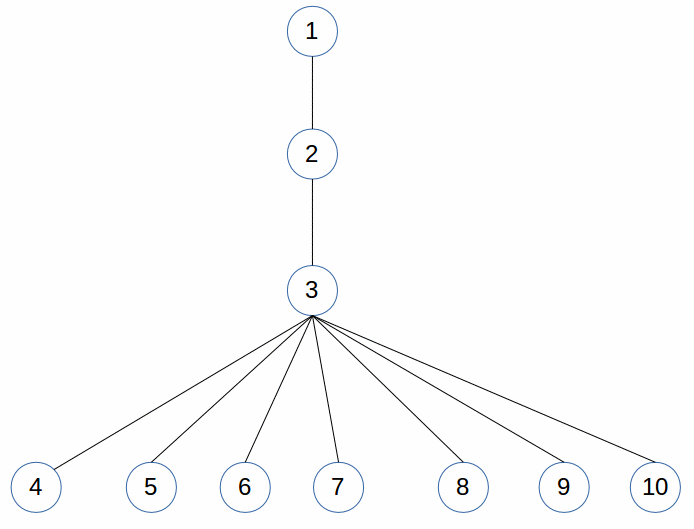
1 - 2 - 6as a longest path, while it is not longest. It is looks like you are trying to find all paths from each final nodes. All path between 1, 6, and 5 nodes in your example. They are not longest. – Interactnnodes andn-1edges. Then you have gotC(n-1, 2)unique longest paths. So the lower limit of complexity is still O(n^2) – Buttonhook