Calculate Torque Required To Align Two 3D Vectors with Constant Acceleration?

Question

I'm currently building a simplified Reaction Control System for a Satellite game, and need a way to use the system to align the satellite to a given unit direction in world-space coordinates. Because this is a game simulation, I am faking the system and just applying a torque force around the objects epicenter.

This is difficult because in my case, the Torque cannot be varied in strength, it is either on or off. It's either full force or no force. Calculating the direction that the torque needs to be applied in is relatively easy, but I'm having trouble getting it to align perfectly without spinning out of control and getting stuck in a logical loop. it needs to apply the opposing force at precisely the right 'time' to land on the target orientation with zero angular velocity.

What I've determined so far is that I need to calculate the 'time' it will take to reach zero velocity based on my current angular velocity and the angle between the two vectors. If that exceeds the time until I reach angle zero, then it needs to apply the opposing torque. In theory this will also prevent it from 'bouncing' around the axis too much. I almost have it working, but in some cases it seems to get stuck applying force in one direction, so I'm hoping somebody can check the logic. My simulation does NOT take mass into account at the moment, so you can ignore the Inertia Tensor (unless it makes the calculation easier!)

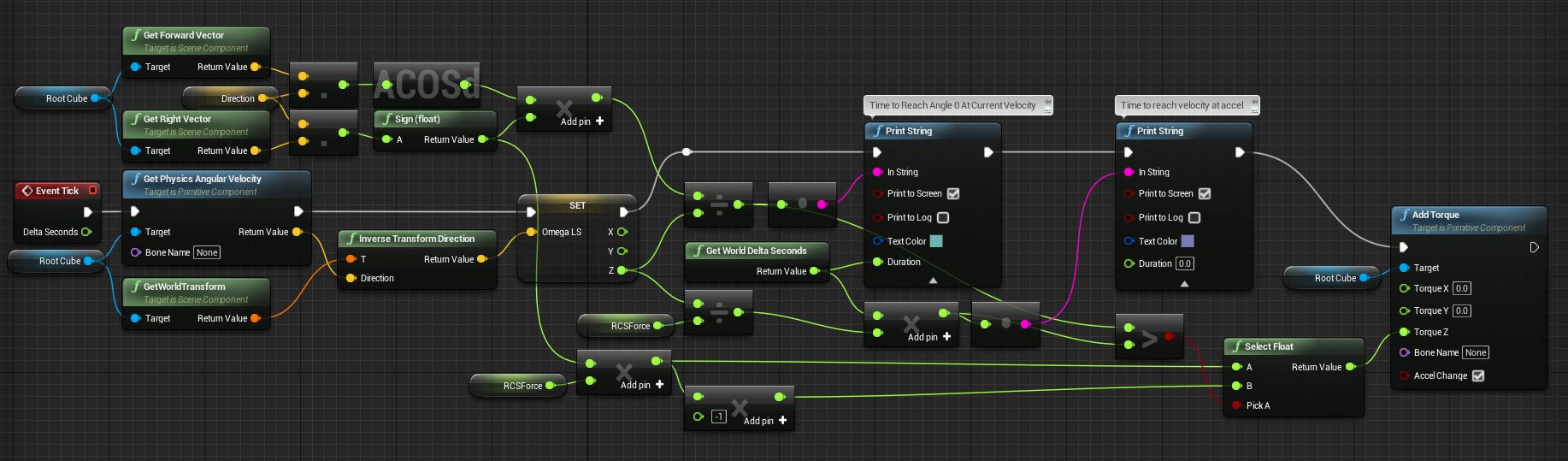
For one axis, I'm currently doing it this way, but I figure someone will have a far more elegant solution that can actually compute both Yaw and Pitch axes at once (Roll is invalid).

Omega = Angular Velocity in Local-Space (Degrees Per Second)
Force = Strength of the Thrusters

// Calculate Time Variables
float Angle = AcosD(DotProduct(ForwardVector, DirectionVector));
float Time1 = Abs(Angle / Omega.Z); // Time taken to reach angle 0 at current velocity
float Time2 = Abs(DeltaTime * (Omega.Z / Force); // Time it will take to reach Zero velocity based on force strength.

// Calculate Direction we need to apply the force to rotate toward the target direction. Note that if we are at perfect opposites, this will be zero!
float AngleSign = Sign(DotProduct(RightVector, DirectionVector));

float Torque.Z = 0;
if (Time1 < Time2)
{
   Torque.Z = AngleSign * Force;
}
else
{
   Torque.Z = AngleSign * Force * -1.0f
}

// Torque is applied to object as a change in acceleration (no mass) and modified by DeltaSeconds for frame-rate independent force. 

This is far from elegant and there are definitely some sign issues. Do you folks know a better way to achieve this?

EDIT: If anybody understands Unreal Engine's Blueprint system, this is how I'm currently prototyping it before I move it to C++

Brasca

Hmm shouldn't Time1 < Time2 be Time1 > Time2? Because this way it would be like "Continue as long as you have enough time to break" or am i wrong? Or is the equation in the if the break and the one multiplied by -1.0f the acceleration? – Muscular

The order of those would definitely matter in the final equation but the main purpose above in the psuedo-code is to highlight that at some point the direction of the force needs to change. – Brasca

Answer 1

Beginning from the "Calculate Direction" line, you could instead directly compute the correction torque vector in 3D, then modify its sign if you know that the previous correction is about to overshoot:

// Calculate Direction we need to apply the force to rotate toward the target direction
Torque = CrossProduct(DirectionVector, ForwardVector)
Torque = Normalize(Torque) * Force
if (Time2 < Time1)
{
  Torque = -Torque
}

But you should handle the problematic cases:

// Calculate Direction we need to apply the force to rotate toward the target direction
Torque = CrossProduct(DirectionVector, ForwardVector)

if (Angle < 0.1 degrees)
{
  // Avoid divide by zero in Normalize
  Torque = {0, 0, 0}
}
else
{
  // Handle case of exactly opposite direction (where CrossProduct is zero)
  if (Angle > 179.9 degrees)
  {
    Torque = {0, 0, 1}
  }

  Torque = Normalize(Torque) * Force
  if (Time2 < Time1)
  {
    Torque = -Torque
  }
}

Bayless

Thanks Saul, I was handling the opposite case differently but this is certainly cleaner so far. Is there a better way to calculate the two time values, or a nicer way to calculate when the direction should be flipped? Although the time values seem correct, there is an issue right now where it will 'land' on the correct direction at zero velocity, but will then start spinning again regardless, and after that it never lands on zero again. – Brasca

Answer 2

Okay well what i take from the pseudocode above is that you want to start braking when the time needed to break exceeds the time left till angle 0 is reached. Have you tried to slowly start breaking (in short steps because of the constant torque) BEFORE the time to break exceeds the time till angle 0?

When you do so and your satellite is near angle 0 and the velocity very low, you can just set velocity and angle to 0 so it doesn't wobble around anymore.

Muscular

Answer 3

Did you ever figure this out? I'm working on a similar problem in UE4. I also have a constant force. I'm rotating to a new forward vector. I've realized time can't be predicted. Take for example you're rotating on Z axis at 100 degrees/second and a reverse force in exactly .015 seconds will nail your desired rotation and velocity but the next frame takes .016 seconds to render and you've just overshot it since you aren't changing your force. I think the solution is something like cheating by manually setting the forward vector once velocity is zeroed out.

Zuzana

Unfortunately I didn't, I ended up going with a spring-like approach and trying to disguise it as best as possible to match up to the Torque system, it's very far from perfect though. I think the problem is because game-time is not infinitely precise, so you can never hit the 'exact' transfer point where you need to 'fire' the opposite direction. I spent a long time on it, but it just didn't work. – Brasca