Clustering overlapping ellipses

Question

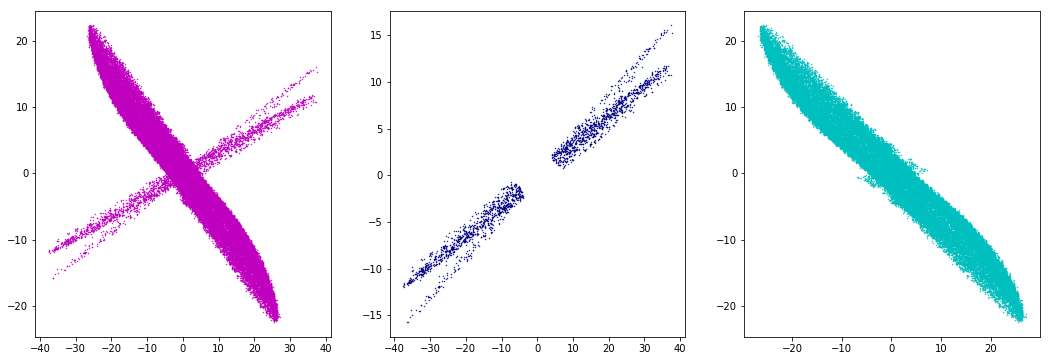
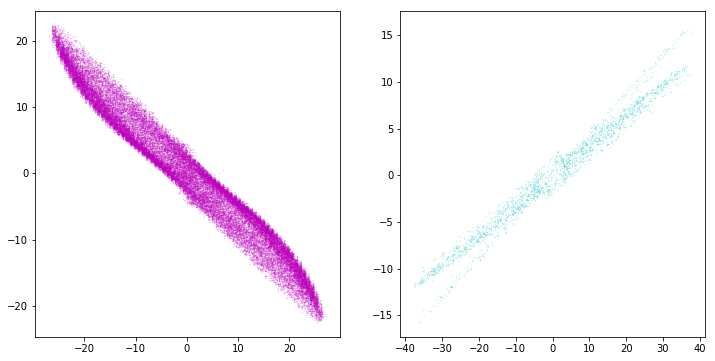I have a data set, which consists of more than one subsets of data. If I plot Y vs. X, I get few overlapping ellipses and I want to cluster them*.

I have tried with the mixture from sklearn, the Bayesian Gaussian Mixture Model gives the best result, however, it does not recognize the overlapping data:

import itertools
import numpy as np
import pylab as plt
from sklearn import mixture
from matplotlib.patches import Ellipse
field_File_1 = './dummy_distrib_3.txt' 
'''
    link to data: 
    https://www.dropbox.com/s/jd3wx1ee8r1mj8p/dummy_distrib_3.txt?dl=0
'''
my_dis_1 = np.loadtxt(field_File_1)

X = my_dis_1[:50000,:2]

BaGaMiMo = mixture.BayesianGaussianMixture(n_components=2, covariance_type='full', 
                                         weight_concentration_prior_type='dirichlet_distribution').fit(X)

X1 = X[BaGaMiMo.predict(X) == 0, :]
X2 = X[BaGaMiMo.predict(X) == 1, :]

plt.figure(figsize=(18.0, 6.0))
plt.subplot(1,3,1)
plt.scatter(X[:,0], X[:,1], 0.2, color='m')

plt.subplot(1,3,2)
plt.scatter(X[BaGaMiMo.predict(X) == 0, 0], X[BaGaMiMo.predict(X) == 0, 1], .2, color='navy')

plt.subplot(1,3,3)
plt.scatter(X[BaGaMiMo.predict(X) == 1, 0], X[BaGaMiMo.predict(X) == 1, 1], .2, color='c')
plt.show()

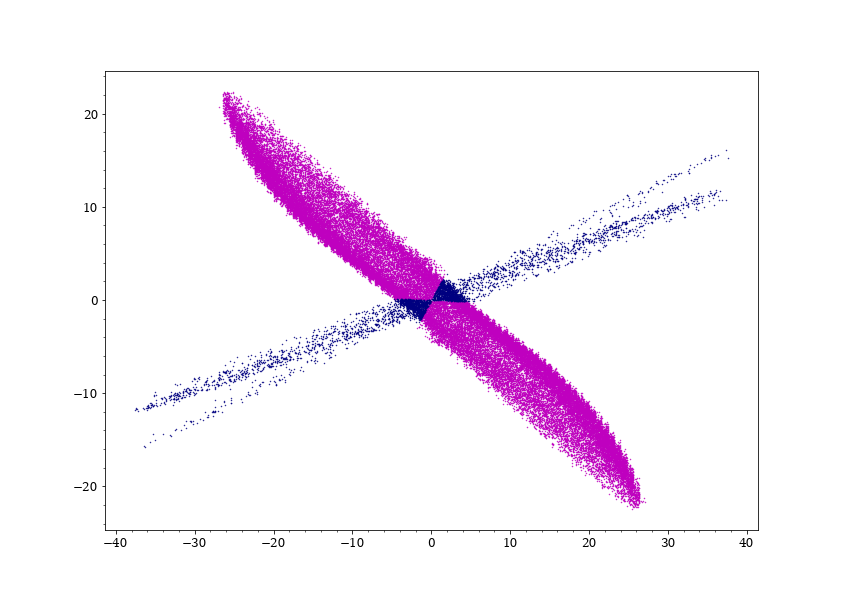
What I do next, is to fit two ellipses to the cyan and navy colored distribution and remove the particles in the cross-section from the cyan distribution,

then assign them randomly to the navy and cyan distributions with the calculated ratio:

One issue is that If I do a histogram of the data, I notice that there is an over-population/discontinuity in the cyan data at the intersection line of the two ellipses and I am looking for ways to reduce that over-population, any help is appreciated.

The jupyter-notebook could be downloaded here: https://www.dropbox.com/s/z1tdgpx1g1lwtb5/Clustering.ipynb?dl=0

.* The data points belong to two sets of charged particles.

Undercut

Besides proximity, ts there any form of relationship within the points belonging to the cyan distribution ? Likewise, is there any relationship within the data points which belong to the navy distribution ? – Mass

The reason for my earlier question is as follows: Consider the cyan data set to be all boys standing in a football pitch and navy data set to be all girls. If such a relationship were to be found, then identifying the cyan and navy clusters is super easy. The question boils down to appropriate feature engineering. – Mass

In my opinion, this problem could be solved through appropriate feature engineering and then finding a good distance function which can give you a clean cyan and a clean navy cluster. – Mass

@Sau001, the two sets of points belong to two different species, however, the whole clustering is to diagnose which point belong to which species. – Undercut

Understood. If you can determine some other feature attribute or a which makes points in Cluster1 distinguishable from points in Cluster2 , then this could be solved by spectral clustering methods where you build up a similarity matrix. en.wikipedia.org/wiki/Spectral_clustering . Otherwise, it would just be a random guess as to which cluster does a point in the intersection region belong to. – Mass

I am afraid I am left (and would be happy) with the random selection. – Undercut

Answer 1

Maybe this will help. I used predict_proba() instead of predict() to get the probabilities that a point belongs to either group. Then I played with the cutoff. Setting the cutoff to 0.5, I got the same results as you. After some trial and error, a cutoff of 0.933 seems to do the trick.

p1 = X[BaGaMiMo.predict_proba(X)[:,0] > 0.933, :]
p2 = X[BaGaMiMo.predict_proba(X)[:,0] <= 0.933, :]
plt.scatter(p1[:,0], p1[:,1], 0.2, color='m')
plt.scatter(p2[:,0], p2[:,1], 0.2, color='navy')

Heirship

I am getting an "IndexError: too many indices for array" on the first line – Undercut

@Undercut predict_proba() returns an array with probabilities for each group, only need one. I fixed the code in the answer. – Heirship

Now I get your result, the mixture is still there. The desired outcome is something like the last pair of plots in the question. – Undercut