Why do Python/Numpy require a row vector for matrix/vector dot product?

Question

Assume we want to compute the dot product of a matrix and a column vector:

So in Numpy/Python here we go:

a=numpy.asarray([[1,2,3], [4,5,6], [7,8,9]])
b=numpy.asarray([[2],[1],[3]])
a.dot(b)

Results in:

array([[13], [31], [49]])

So far, so good, however why is this also working?

b=numpy.asarray([2,1,3])
a.dot(b)

Results in:

array([13, 31, 49])

I would expect that [2,1,3] is a row vector (which requires a transpose to apply the dot product), but Numpy seems to see arrays by default as column vectors (in case of matrix multiplication)?

How does this work?

EDIT:

And why is:

b=numpy.asarray([2,1,3])
b.transpose()==b

So the matrix dot vector array does work (so then it sees it as a column vector), however other operations (transpose) does not work. This is not really consistent design isn't it?

Outguess

Related question: #17429121 – Hateful

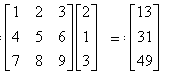
array([2, 1, 3]) isn't a row vector or a column vector. It's just a vector. – Pizzicato

@Pizzicato should you even call it a vector? I think that's the main source of this often-seen confusion. By "vector" people usually refer to an [n x 1] or [1 x n] object. But as I see it, the point is exactly that a 1d ndarray has a single dimension, so I'd say that it's not a vector, but an array. (And sure, there are special nd arrays which can be thought of as vectors or matrices, namely with n==2:) – Expand

What happens with ``[[1,2,3]]`? – Mescal

Answer 1

Let's first understand how the dot operation is defined in numpy.

(Leaving broadcasting rules out of the discussion, for simplicity) you can perform dot(A,B) if the last dimension of A (i.e. A.shape[-1]) is the same as the next-to-last dimension of B (i.e. B.shape[-2]) if B.ndim>=2, and simply the dimension of B if B.ndim==1.

In other words, if A.shape=(N1,...,Nk,X) and B.shape=(M1,...,M(j-1),X,Mj) (note the common X). The resulting array will have the shape (N1,...,Nk,M1,...,Mj) (note that X was dropped).

Or, if A.shape=(N1,...,Nk,X) and B.shape=(X,). The resulting array will have the shape (N1,...,Nk) (note that X was dropped).

Your examples work because they satisfy the rules (the first example satisfies the first, the second satisfies the second):

a=numpy.asarray([[1,2,3], [4,5,6], [7,8,9]])
b=numpy.asarray([[2],[1],[3]])
a.shape, b.shape, '->', a.dot(b).shape  # X=3
=> ((3, 3), (3, 1), '->', (3, 1))

b=numpy.asarray([2,1,3])
a.shape, b.shape, '->', a.dot(b).shape  # X=3
=> ((3, 3), (3,), '->', (3,))

---

My recommendation is that, when using numpy, don't think in terms of "row/column vectors", and if possible don't think in terms of "vectors" at all, but in terms of "an array with shape S". This means that both row vectors and column vectors are simply "1dim arrays". As far as numpy is concerned, they are one and the same.

This should also make it clear why in your case b.transponse() is the same as b. b being a 1dim array, when transposed, remains a 1dim array. Transpose doesn't affect 1dim arrays.

Reactant

That's not how numpy.dot treats arguments of dimension higher than 2. I recommend just leaving the high-dimension behavior out of your answer; dot's high-dimension behavior isn't very useful. – Pizzicato

@user2357112, thanks for pointing that out. I fixed my answer. – Reactant

@Pizzicato "dot's high-dimension behavior isn't very useful" - maybe not to you! – Atlantic

Transpose not working on 1D arrays is the most annoying thing for anybody who switches to numpy from any other software/language. 1D arrays should have been the exception in my opinion instead of the default. – Allanadale

@Allanadale I find a[:,None] quite straightforward once you encounter it. Since 1d arrays don't have a defined orientation (row/column), I see the reason for their transpose not being defined (even though 1d arrays are usually equivalent to row vectors...). – Expand

@AndrasDeak Yes but if I take the time to create an array it's rare that I want to make it a 1D array. The whole manual array input is based on creating vectors and I find it stupid to write [[1],[0],[0]] many brackets to have a column – Allanadale

@Allanadale you could write array([1,0,0])[:,None];) But I get your point. – Expand

@AndrasDeak Instead I go with atleast_2D and auto complete props. – Allanadale