Smoothing my heatmap in Python

Question

I am developing a script in order to make heatmap from a sky survey with python and the libraries numpy, astropy.

I created a stars distribution map and now I'm trying to make a heatmap. My heatmap is done and works well, but my next step is to smooth it with a Gaussian. That's to say, convolute the data by a Gaussian with dispersion = 2 sigma.

The problem is I don't get a good smoothing heatmap. As you could see after, my plots are not good with the convolution function by scipy and/or astropy (I scripted both methods).

This is my code:

# -*- coding: utf-8 -*-
#!/usr/bin/env python

from astropy.io import fits
from astropy.table import Table
from astropy.table import Column
from astropy.convolution import convolve, Gaussian1DKernel
import numpy as np
import scipy.ndimage as sp
import matplotlib.pyplot as plt



        ###################################
        # Importation du fichier de champ #
        ###################################

filename = '/home/valentin/Desktop/Field169_combined_final_roughcal.fits_traite_traiteXY_traiteXY_final'

print 'Fichier en cours de traitement' + str(filename) + '\n'

# Ouverture du fichier à l'aide d'astropy
field = fits.open(filename)        

# Lecture des données fits 
tbdata = field[1].data            


        #######################################
        # Parametres pour la carte de densité #
        #######################################

# Boite des étoiles bleues :
condition_1 = np.bitwise_and(tbdata['g0-r0'] > -0.5, tbdata['g0-r0'] < 0.8 )  # Ne garder que les -0.4 < (g-r)0 < 0.8
condition_final = np.bitwise_and(tbdata['g0'] < 23.5, condition_1)       # Récupere les valeurs de 'g0' < 23.5 dans les valeurs de blue_stars_X

Blue_stars = tbdata[condition_final]

RA_Blue_stars = Blue_stars['RA']                        # Récupere les valeurs de 'RA' associées aux étoiles bleues
DEC_Blue_stars = Blue_stars['DEC']                      # Récupere les valeurs de 'DEC' associées aux étoiles bleues


# Boite des étoiles tres bleues :
condition_2 = np.bitwise_and(tbdata['g0-r0'] > -0.5, tbdata['g0-r0'] < 0.2 )
condition_final2 = np.bitwise_and(tbdata['g0'] < 23.5, condition_2)

Very_Blue_stars = tbdata[condition_final2]

RA_Very_Blue_stars = Very_Blue_stars['RA']                      # Récupere les valeurs de 'RA' associées aux étoiles bleues
DEC_Very_Blue_stars = Very_Blue_stars['DEC']

# ==> La table finale avec le masque s'appelle Blue_stars & Very_Blue_stars

        ##################################################################
        # Traçage des différents graphiques de la distribution d'étoiles #
        ##################################################################


fig1 = plt.subplot(2,2,1)
plt.plot(tbdata['g0-r0'], tbdata['g0'], 'r.', label=u'Etoiles du champ')
plt.plot(Blue_stars['g0-r0'], Blue_stars['g0'], 'b.', label =u'Etoiles bleues')
plt.plot(Very_Blue_stars['g0-r0'], Very_Blue_stars['g0'], 'k.', label =u'Etoiles tres bleues')
plt.title('Diagramme Couleur-Magnitude')
plt.xlabel('(g0-r0)')
plt.ylabel('g0')
plt.xlim(-1.5,2.5)
plt.ylim(14,28)
plt.legend(loc='upper left')
plt.gca().invert_yaxis()

fig1 = plt.subplot(2,2,2)
plt.plot(RA_Blue_stars, DEC_Blue_stars, 'b.', label =u'Etoiles bleues', alpha=0.15)
plt.title('Carte de distribution des etoiles bleues')
plt.xlabel('RA')
plt.ylabel('DEC')
plt.legend(loc='upper left')

fig1 = plt.subplot(2,2,3)
plt.plot(RA_Very_Blue_stars, DEC_Very_Blue_stars, 'r.', label =u'Etoiles tres bleues',alpha=0.4)
plt.title('Carte de distribution des etoiles tres bleues')
plt.xlabel('RA')
plt.ylabel('DEC')
plt.legend(loc='upper left')

fig1 = plt.subplot(2,2,4)
plt.plot(RA_Blue_stars, DEC_Blue_stars, 'b.', label =u'Etoiles bleues', alpha=0.15)
plt.plot(RA_Very_Blue_stars, DEC_Very_Blue_stars, 'r.', label =u'Etoiles tres bleues',alpha=0.4)
plt.title('Carte de distribution des etoiles bleues et tres bleues')
plt.xlabel('RA')
plt.ylabel('DEC')
plt.legend(loc='upper left')

        ######################################################################
        # Traçage des différents graphiques de la carte de densité d'étoiles #
        ######################################################################

###############################################################################
# Carte de densité des étoiles bleues pour 1 pixel de 1 arcmin^2 (bins = 180) #
###############################################################################

X_Blue_stars = Blue_stars['X']
Y_Blue_stars = Blue_stars['Y']

heatmap, xedges, yedges = np.histogram2d(X_Blue_stars, Y_Blue_stars, bins=180) # bins de 180 car 3° de champ en RA = 180 arcmin de champ en RA
extent = [xedges[0], xedges[-1], yedges[0], yedges[-1]]

plt.clf()
plt.subplot(2,2,1)
plt.imshow(heatmap, extent=extent)
plt.colorbar()
plt.title('Carte de densite des etoiles bleues (non lisse)')
plt.xlabel("X")
plt.ylabel("Y")
plt.gca().invert_xaxis()


####################################################################################################################################
# Carte de densité lissée (par convolution avec une gaussienne 2 sigma) des étoiles bleues pour 1 pixel de 1 arcmin^2 (bins = 180) #
# ==> Avec Scipy                                                        #
####################################################################################################################################

lissage_X_scipy = sp.filters.gaussian_filter(X_Blue_stars, sigma = 2, order = 0)
lissage_Y_scipy = sp.filters.gaussian_filter(Y_Blue_stars, sigma = 2, order = 0)


heatmap_lisse_scipy, xedges_lisse_scipy, yedges_lisse_scipy = np.histogram2d(lissage_X_scipy, lissage_Y_scipy, bins=180)
extent_lisse_scipy = [xedges_lisse_scipy[0], xedges_lisse_scipy[-1], yedges_lisse_scipy[0], yedges_lisse_scipy[-1]]

plt.subplot(2,2,2)
plt.imshow(heatmap_lisse_scipy, extent=extent_lisse_scipy)
plt.colorbar()
plt.title('Carte de densite des etoiles bleues lisse a 2 sigma (scipy)')
plt.xlabel("X")
plt.ylabel("Y")
plt.gca().invert_xaxis()

####################################################################################################################################
# Carte de densité lissée (par convolution avec une gaussienne 2 sigma) des étoiles bleues pour 1 pixel de 1 arcmin^2 (bins = 180) #
# ==> Avec Astropy                                                          #
####################################################################################################################################

# Creation du kernel :

K = Gaussian1DKernel(stddev=2) # Détermination de la déviation standard (sigma)

lissage_X_astropy = convolve(X_Blue_stars, kernel=K, boundary='fill')
lissage_Y_astropy = convolve(Y_Blue_stars, kernel=K, boundary='fill')

heatmap_lisse_astropy, xedges_lisse_astropy, yedges_lisse_astropy = np.histogram2d(lissage_X_astropy, lissage_Y_astropy, bins=180)
extent_lisse_astropy = [xedges_lisse_astropy[0], xedges_lisse_astropy[-1], yedges_lisse_astropy[0], yedges_lisse_astropy[-1]]

plt.subplot(2,2,3)
plt.imshow(heatmap_lisse_astropy, extent=extent_lisse_astropy)
plt.colorbar()
plt.title('Carte de densite des etoiles bleues lisse (astropy)')
plt.xlabel("X")
plt.ylabel("Y")
plt.gca().invert_xaxis()
plt.show()

print "Création du Diagramme"

I get this :

1. Top left: heatmap without smoothing
2. Top right: heatmap with scipy smoothing
3. Bottom: heatmap with astropy smoothing

I don't know why, there are lots of holes, lacks ... with the smoothing :/

UPDATE:

After the answer from Framester, I wrote an easier script which contains the "same thing" that my problem. I applied the same method (by scipy for example) and I get a smoothing heatmap :)

import matplotlib.pyplot as plt
import numpy as np
import scipy.ndimage as sp


x = np.random.randn(100000)
y = np.random.randn(100000) + 5

# normal distribution center at x=0 and y=5
fig1 = plt.subplot(2,2,1)
plt.hist2d(x, y, bins=40)
plt.colorbar()
plt.title('Heatmap without smoothing')
plt.xlabel("X")
plt.ylabel("Y")


# smoothing

X = sp.filters.gaussian_filter(x, sigma = 2, order = 0)
Y = sp.filters.gaussian_filter(y, sigma = 2, order = 0)


heatmap, xedges, yedges = np.histogram2d(X, Y, bins=40)
extent = [xedges[0], xedges[-1], yedges[0], yedges[-1]]

fig1 = plt.subplot(2,2,2)
plt.imshow(heatmap, extent=extent)
plt.colorbar()
plt.title('Heatmap with smoothing')
plt.xlabel("X")
plt.ylabel("Y")
plt.show()

So, my question is : why my script doesn't work ? :/

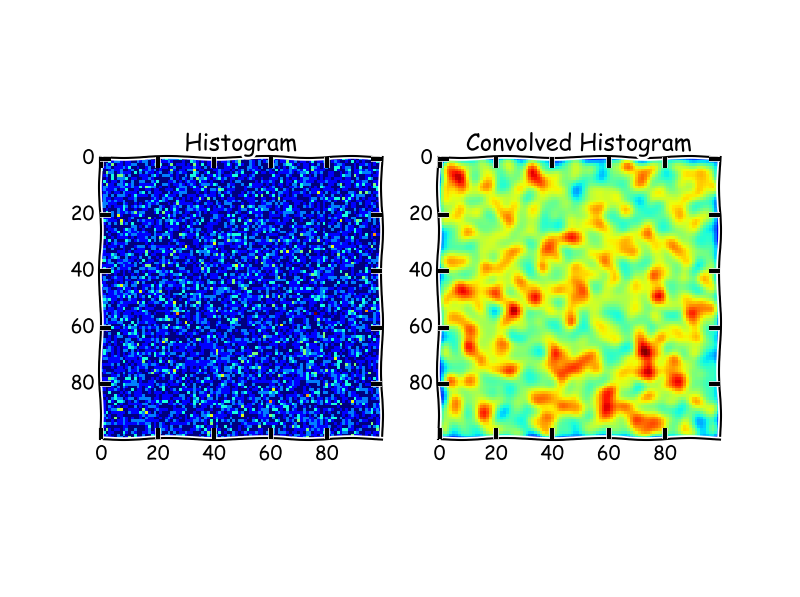
SOLUTION BY MSEIFERT :

plt.clf()
plt.subplot(2,2,1)
plt.imshow(heatmap, extent=extent, interpolation='none')
plt.colorbar()
plt.title('Carte de densite des etoiles bleues (non lisse)')
plt.xlabel("X")
plt.ylabel("Y")
plt.gca().invert_xaxis()

plt.subplot(2,2,2)
plt.imshow(convolve(heatmap, Gaussian2DKernel(stddev=2)), interpolation='none')
plt.colorbar()
plt.title('Carte de densite des etoiles bleues lisse (astropy)')
plt.xlabel("X")
plt.ylabel("Y")
plt.gca().invert_xaxis()

plt.show()

Greenhouse

Try a minimal example using a randomly generated image and try to smooth that. This should be only a couple of lines, so an error will be much easier to spot and other people can easilier reproduce the behaviour. Good luck! – Behr

@ Framester I will try later ;) But, it is the same thing that this exemple in astropy doc : docs.astropy.org/en/stable/convolution I take this website as exemple in order to make my script, I get a smoothing, but not what I want :/ So, if people have lots of ideas during I making that, you're welcome :) – Greenhouse

Maybe using this will help: scipy.github.io/old-wiki/pages/Cookbook/RadialBasisFunctions – Bumf

FYI the correct term is "convolve", although "convolutate" does have a nice ring to it.. – Aftergrowth

How to interpret the colorbar after smoothing? – Transoceanic

Answer 1

The main problem is that your X_Blue_stars and Y_Blue_stars are tabulated values, while the convolution is something that should be applied to signals (i.e. images). Just for illustration suppose you have 10 tabulated x and y coordinates:

x = np.array([3, 3, 4, 4, 4, 5, 5, 5, 9, 9])
y = np.array([9, 0, 0, 4, 7, 5, 5, 9, 0, 2])

if you apply a Gaussian filter on them the coordinates of different stars are getting convolved:

from astropy.convolution import convolve
from astropy.convolution.kernels import Gaussian1DKernel
convolve(x, Gaussian1DKernel(stddev=2))
#array([ 2.0351543 ,  2.7680258 ,  3.40347329,  3.92589723,  4.39194033,
#        4.86262055,  5.31327857,  5.56563858,  5.34183035,  4.48909886])
convolve(y, Gaussian1DKernel(stddev=2))
#array([ 2.30207128,  2.72042232,  3.17841789,  3.78905438,  4.42883559,
#        4.81542569,  4.71720663,  4.0875217 ,  3.08970732,  2.01679469])

which is almost certainly NOT what you want. You probably want to convolve your heatmap (this time I chose a rather larger sample to have some nice plots):

x = np.random.randint(0,100,10000)
y = np.random.randint(0,100,10000)

heatmap, xedges, yedges = np.histogram2d(x, y, bins=100)

Now plot the original histogram

fig, (ax1, ax2) = plt.subplots(1, 2)
ax1.imshow(heatmap, interpolation='none')

and the convolved heatmap

from astropy.convolution.kernels import Gaussian2DKernel
ax2.imshow(convolve(heatmap, Gaussian2DKernel(stddev=2)), interpolation='none')
plt.show()

which gives me (forgive me the use of plt.xkcd):

Castaneda

It's perfect ! I believed that I should convolve my data and plot it after. But now, I understand very well and I get a very good smoothed heatmap ! Thank you :) – Greenhouse