Providing a candidate solution to this very interesting problem using example data below. To fit the penalised VAR I've used the recently released BigVAR package. At this point it doesn't come with the usual extra functionality of producing FEVDs, historical decomps, prediction fancharts etc., but all the necessary output from the reduced-form model can be obtained through cv.BigVAR. This is what I've done as a first step below. I'll leave it to yourself to finetune the reduced-form estimation using the package functionality.
# BigVAR ----
library(BigVAR)
library(expm)
library(data.table)
# Create model
data(Y)
p = 4 # lags
k = ncol(Y) # number of equations
N = nrow(Y) - p # number of obs
# Create a Basic VAR-L (Lasso Penalty) with maximum lag order p=4, 10 gridpoints with lambda optimized according to rolling validation of 1-step ahead MSFE
mod1 = constructModel(Y,p,"Basic",gran=c(150,10),RVAR=FALSE,h=1,cv="Rolling",MN=FALSE,verbose=FALSE,IC=TRUE)
results = cv.BigVAR(mod1)
# Get model estimates
A = results@betaPred[,2:ncol(results@betaPred)] # (k x (k*p)) = (3 x (3*4)) coefficient matrix (reduced form)
Sigma = crossprod(resid(varres))/(N-(k*p)-1)
From there we can use standard formulas to compute the FEVDs. For an accessible introduction I would highly recommend Chapter 4 of 'Structural Vector Autoregressive Analysis' by Lutz Kilian and Helmut Lütkepohl. The below implements everything we need from reduced-form IRFs to the MSPE and finally our formula to compute the FEVD in R. This will may be a lot to take in and I haven't had time to polish this code so this may well be done more efficiently, but hopefully it's still informative. Note that I am using a standard Choleski decomposition to identify the VAR so the usual implications of the ordering of the variables apply.
# A number of helper functions ----
# Compute reduced-form IRFs:
compute_Phi = function(p, k, A_comp, n.ahead) {
J = matrix(0,nrow=k,ncol=k*p)
diag(J) = 1
Phi = lapply(1:n.ahead, function(i) {
J %*% (A_comp %^% (i-1)) %*% t(J)
})
return(Phi)
}
# Compute orthogonalized IRFs:
compute_theta_kj_sq = function(Theta, n.ahead) {
theta_kj_sq = lapply(1:n.ahead, function(h) { # loop over h time periods
out = sapply(1:ncol(Theta[[h]]), function(k) {
terms_to_sum = lapply(1:h, function(i) {
Theta[[i]][k,]**2
})
theta_kj_sq_h = Reduce(`+`, terms_to_sum)
})
colnames(out) = colnames(Theta[[h]])
return(out)
})
return(theta_kj_sq)
}
# Compute mean squared prediction error:
compute_mspe = function(Theta, n.ahead=10) {
mspe = lapply(1:n.ahead, function(h) {
terms_to_sum = lapply(1:h, function(i) {
tcrossprod(Theta[[i]])
})
mspe_h = Reduce(`+`, terms_to_sum)
})
}
# Function for FEVD:
fevd = function(A, Sigma, n.ahead) {
k = dim(A)[1] # number of equations
p = dim(A)[2]/k # number of lags
# Turn into companion form:
if (p>1) {
A_comp = VarptoVar1MC(A,p,k)
} else {
A_comp = A
}
# Compute MSPE: ----
Phi = compute_Phi(p,k,A_comp,n.ahead)
P = t(chol.default(Sigma)) # lower triangular Cholesky factor
B_0 = solve(P) # identification matrix
Theta = lapply(1:length(Phi), function(i) {
Phi[[i]] %*% solve(B_0)
})
theta_kj_sq = compute_theta_kj_sq(Theta, n.ahead) # Squared orthogonaliyed IRFs
mspe = compute_mspe(Theta, n.ahead)
# Compute percentage contributions (i.e. FEVDs): ----
fevd_list = lapply(1:k, function(k) {
t(sapply(1:length(mspe), function(h) {
mspe_k = mspe[[h]][k,k]
theta_k_sq = theta_kj_sq[[h]][,k]
fevd = theta_k_sq/mspe_k
}))
})
# Tidy up
fevd_tidy = data.table::rbindlist(
lapply(1:length(fevd_list), function(k) {
fevd_k = data.table::melt(data.table::data.table(fevd_list[[k]])[,h:=.I], id.vars = "h", variable.name = "j")
fevd_k[,k:=paste0("V",k)]
data.table::setcolorder(fevd_k, c("k", "j", "h"))
})
)
return(fevd_tidy)
}
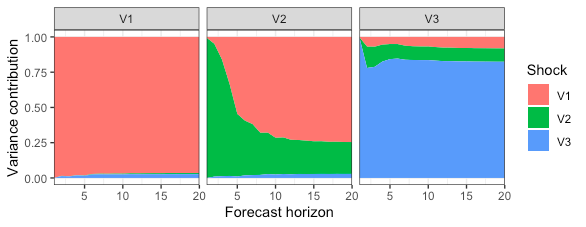
Lastly, lets implement the formula for n.ahead=20 and plot the results.
fevd_res = fevd(A, Sigma, 20)
library(ggplot2)
p = ggplot(data=fevd_res) +
geom_area(aes(x=h, y=value, fill=j)) +
facet_wrap(k ~ .) +
scale_x_continuous(
expand=c(0,0)
) +
scale_fill_discrete(
name = "Shock"
) +
labs(
y = "Variance contribution",
x = "Forecast horizon"
) +
theme_bw()
p
![FEVD plots]()
Hope this is helpful and please shout if any follow-up questions.
Finally a note of caution: I have tested the FEVD function by comparing it to the results for a standard VAR using the vars package that you mention in your question and it checks out (see below). But this is as far as my "unit-testing" has gone. The code has not been reviewed by anyone so just be aware of that and perhaps dig through the formulas yourself. If you or anyone else spots any errors, I'd be grateful for feedback.
Edit 1
For the sake of completeness adding a quick comparison of results returned by vars::fevd and the custom function from above.
# Compare to vars package ----
library(vars)
p = 4 # lags
k = ncol(Y) # number of equations
N = nrow(Y) - p
colnames(Y) = sprintf("V%i", 1:ncol(Y))
n.ahead = 20
varres = vars::VAR(Y,p) # reduced-form model using package command; vars:: to make clear that pkg
# Get estimates for custom fevd function:
Sigma = crossprod(resid(varres))/(N-(k*p)-1)
A = t(
sapply(coef(varres), function(i) {
i[,1]
})
)
A = A[,1:(ncol(A)-1)]
# Run the two different functions:
fevd_pkg = vars::fevd(varres, n.ahead)
fevd_cus = fevd(A, Sigma, n.ahead)
Now comparing the outputs for the first variable:
> # Package:
> head(fevd_pkg$V1)
V1 V2 V3
[1,] 1.0000000 0.00000000 0.00000000
[2,] 0.9399842 0.01303013 0.04698572
[3,] 0.9422918 0.01062750 0.04708065
[4,] 0.9231440 0.01409313 0.06276291
[5,] 0.9305901 0.01335727 0.05605267
[6,] 0.9093144 0.01278727 0.07789833
> # Custom:
> head(dcast(fevd_cus[k=="V1"], k+h~j, value.var = "value"))
k h V1 V2 V3
1: V1 1 1.0000000 0.00000000 0.00000000
2: V1 2 0.9399842 0.01303013 0.04698572
3: V1 3 0.9422918 0.01062750 0.04708065
4: V1 4 0.9231440 0.01409313 0.06276291
5: V1 5 0.9305901 0.01335727 0.05605267
6: V1 6 0.9093144 0.01278727 0.07789833
Edit 2
To get the generalized FEVD in R without depending on output from vars::VAR(), you can use the function below. I have recycled some of the source code of frequencyConnectedness::genFEVD.
# Generalized FEVD ----
library(frequencyConnectedness)
genFEVD_cus = function(
A,
Sigma,
n.ahead,
no.corr=F
) {
k = dim(A)[1] # number of equations
p = dim(A)[2]/k # number of lags
# Turn into companion form:
if (p>1) {
A_comp = BigVAR::VarptoVar1MC(A,p,k)
} else {
A_comp = A
}
# Set off-diagonals to zero:
if (no.corr) {
Sigma = diag(diag(Sigma))
}
Phi = compute_Phi(p,k,A_comp,n.ahead+1) # Reduced-form irfs
denom = diag(Reduce("+", lapply(Phi, function(i) i %*% Sigma %*%
t(i))))
enum = Reduce("+", lapply(Phi, function(i) (i %*% Sigma)^2))
tab = sapply(1:nrow(enum), function(j) enum[j, ]/(denom[j] *
diag(Sigma)))
tab = t(apply(tab, 2, function(i) i/sum(i)))
return(tab)
}
Continuing from the above example (Edit 1) compare the results from the custom function to results from frequencyConnectedness::genFEVD which depends on the output from vars::VAR():
> frequencyConnectedness::genFEVD(varres, n.ahead)
V1 V2 V3
[1,] 0.89215734 0.02281892 0.08502374
[2,] 0.72025050 0.19335481 0.08639469
[3,] 0.08328267 0.11769438 0.79902295
> genFEVD_cus(A, Sigma, n.ahead)
V1 V2 V3
[1,] 0.89215734 0.02281892 0.08502374
[2,] 0.72025050 0.19335481 0.08639469
[3,] 0.08328267 0.11769438 0.79902295