examining residuals and visualizing zero-inflated poission r

Question

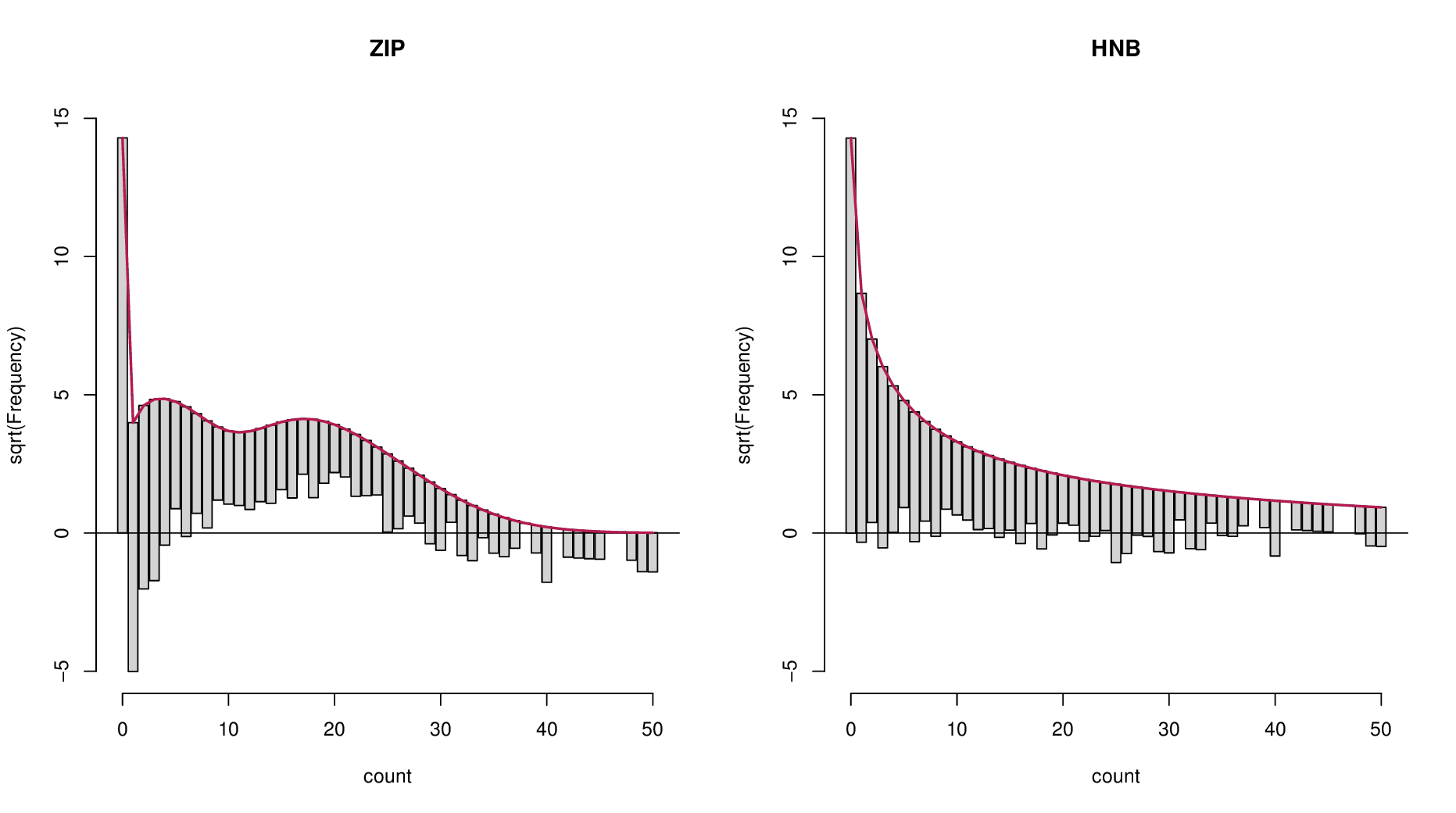
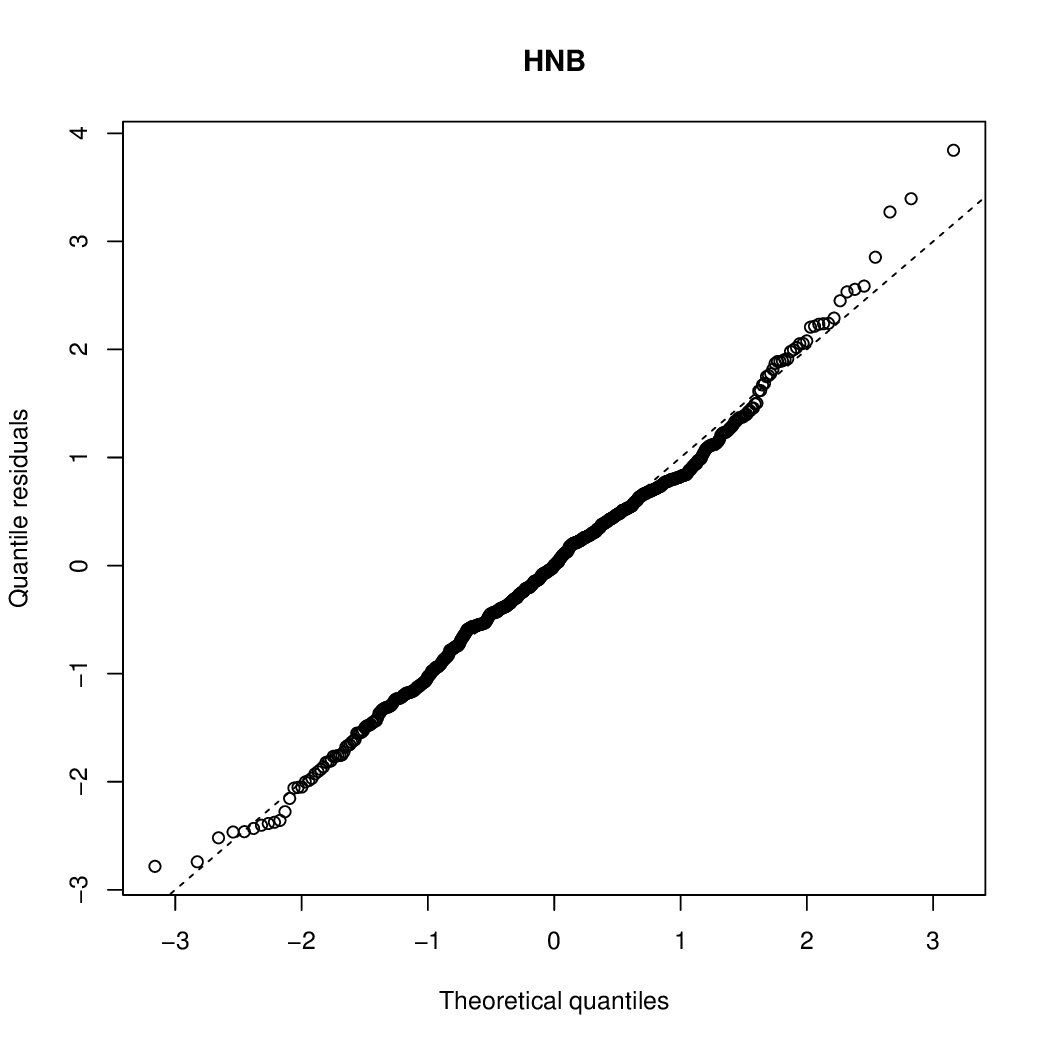
I am running a zero-inflated model for CPUE data. This data has evidence of zero-inflation which I have confirmed with a Vuong test (in code below). The full model (zint) is better than the null according to AIC. I now want to:

1. Examine the residuals of the full model to determine model fit (having trouble due to lack of info from colleagues, internet, and R books)
2. If model fit appears to be okay, visualize the output of the model (how to formulate equations of real-parameter values when using an offset variable)

I have asked help from a few statisticians in the department (they have never done this before and send me to the same google search sites), outside to the stats department itself (everyone is too busy), and stackoverflow feeds.

I would appreciate code or guidance to books (available free online) with code that deal with visualizing ZIPs and model fit when using an offset variable.

 yc=read.csv("CPUE_ycs_trawl_withcobb_BLS.csv",header=TRUE)
 yc=yc[which(yc$countinyear<150),]
 yc$fyear=as.factor(yc$year_cap)
 yc$flocation=as.factor(yc$location)
 hist(yc$countinyear,20)
 yc$logoffset=log(yc$numtrawlyr)

 ###Run Zero-inflated poisson with offset for CPUE####
 null <- formula(yc$countinyear ~ 1| 1)
 znull <- zeroinfl(null, offset=logoffset,dist = "poisson",link = "logit",
 data = yc)

 int <- formula(yc$countinyear ~ assnage * spawncob| assnage * spawncob)
 zint <- zeroinfl(int, offset=logoffset,dist = "poisson",link = "logit", data  
 = yc)
 AIC(znull,zint)

  g1=glm(countinyear ~ assnage * spawncob,
  offset=logoffset,data=yc,family=poisson)
  summary(g1)

 ####Vuong test to see if ZIP is even needed##
 vuong(g1,zint)

 ##########DATASET###########

countinyear is column #1

 ##########DATASET###########

count assnage    spawncob      logoffset
56      0       0.32110173      2.833213
44      1       0.33712     2.833213
60      2       0.34053264      2.833213
0       4       0.19381496      2.833213
1       3       0.30819333      2.833213
33      0       0.32110173      2.833213
40      1       0.33712     2.833213
25      2       0.34053264      2.833213
0       3       0.30819333      2.833213
2       4       0.19381496      2.833213
6       0       0.32110173      2.833213
13      1       0.33712     2.833213
7       2       0.34053264      2.833213
0       3       0.30819333      2.833213
0       4       0.19381496      NA
5       0       0.32110173      2.833213
31      1       0.33712     2.833213
73      2       0.34053264      2.833213
0       3       0.30819333      2.833213
1       4       0.19381496      2.833213
0       0       0.32110173      2.833213
7       1       0.33712     2.833213
75      2       0.34053264      2.833213
3       3       0.30819333      2.833213
0       4       0.19381496      2.833213
19      0       0.32110173      2.833213
13      1       0.33712     2.833213
18      2       0.34053264      2.833213
0       3       0.30819333      2.833213
2       4       0.19381496      2.833213
11      0       0.32110173      2.833213
14      1       0.33712     2.833213
32      2       0.34053264      2.833213
1       3       0.30819333      2.833213
1       4       0.19381496      2.833213
12      0       0.32110173      2.833213
3       1       0.33712     2.833213
9       2       0.34053264      2.833213
2       3       0.30819333      2.833213
0       4       0.19381496      2.833213
5       0       0.32110173      2.833213
15      1       0.33712     2.833213
22      2       0.34053264      2.833213
5       3       0.30819333      2.833213
1       4       0.19381496      2.833213
1       0       0.32110173      2.833213
16      1       0.33712     2.833213
33      2       0.34053264      2.833213
4       3       0.30819333      2.833213
2       4       0.19381496      2.833213
6       0       0.32110173      2.833213
17      1       0.33712     2.833213
26      2       0.34053264      2.833213
1       3       0.30819333      2.833213
0       4       0.19381496      2.833213
16      0       0.32110173      2.833213
16      1       0.33712     2.833213
11      2       0.34053264      2.833213
1       3       0.30819333      2.833213
1       4       0.19381496      2.833213
2       0       0.32110173      2.833213
8       1       0.33712     2.833213
18      2       0.34053264      2.833213
0       3       0.30819333      2.833213
0       4       0.19381496      2.833213
2       0       0.32110173      2.833213
27      1       0.33712     2.833213
49      2       0.34053264      2.833213
1       3       0.30819333      2.833213
0       4       0.19381496      2.833213
1       0       0.32110173      2.833213
6       1       0.33712     2.833213
36      2       0.34053264      2.833213
17      3       0.30819333      2.833213
0       4       0.19381496      2.833213
10      0       0.32110173      2.833213
21      1       0.33712     2.833213
78      2       0.34053264      2.833213
32      3       0.30819333      2.833213
0       4       0.19381496      2.833213
0       0       0.32110173      2.833213
8       1       0.33712     2.833213
14      2       0.34053264      2.833213
7       3       0.30819333      2.833213
0       4       0.19381496      2.833213
0       1       0.13648433      2.833213
6       1       0.23952033      2.833213
12      2       0.32110173      2.833213
0       3       0.33712     2.833213
0       4       0.34053264      2.833213
30      0       0.13648433      2.833213
30      1       0.23952033      2.833213
25      2       0.32110173      2.833213
30      3       0.33712     2.833213
30      4       0.34053264      2.833213
68      0       0.13648433      2.833213
68      1       0.23952033      2.833213
55      2       0.32110173      2.833213
68      3       0.33712     2.833213
68      4       0.34053264      2.833213
0       0       0.13648433      2.833213
12      1       0.23952033      2.833213
26      2       0.32110173      2.833213
2       3       0.33712     2.833213
1       4       0.34053264      2.833213
0       0       0.13648433      2.833213
17      1       0.23952033      2.833213
36      2       0.32110173      2.833213
1       3       0.33712     2.833213
4       4       0.34053264      2.833213
1       0       0.13648433      2.833213
1       1       0.23952033      2.833213
4       2       0.32110173      2.833213
4       3       0.33712     2.833213
0       4       0.34053264      2.833213
3       0       0.13648433      2.833213
3       1       0.23952033      2.833213
3       2       0.32110173      2.833213
3       3       0.33712     2.833213
3       4       0.34053264      2.833213
0       0       0.13648433      2.833213
29      1       0.23952033      2.833213
33      2       0.32110173      2.833213
0       3       0.33712     2.833213
0       4       0.34053264      2.833213
0       0       0.13648433      2.833213
10      1       0.23952033      2.833213
7       2       0.32110173      2.833213
1       3       0.33712     2.833213
0       4       0.34053264      2.833213
0       0       0.13648433      2.833213
6       1       0.23952033      2.833213
18      2       0.32110173      2.833213
1       3       0.33712     2.833213
0       4       0.34053264      2.833213
0       0       0.13648433      2.833213
18      1       0.23952033      2.833213
37      2       0.32110173      2.833213
1       3       0.33712     2.833213
1       4       0.34053264      2.833213
0       0       0.13648433      2.833213
13      1       0.23952033      2.833213
26      2       0.32110173      2.833213
8       3       0.33712     2.833213
0       4       0.34053264      2.833213
0       0       0.13648433      2.833213
0       1       0.23952033      2.833213
1       2       0.32110173      2.833213
0       3       0.33712     2.833213
0       4       0.34053264      2.833213
0       0       0.13648433      2.833213
1       1       0.23952033      2.833213
5       2       0.32110173      2.833213
0       3       0.33712     2.833213
0       4       0.34053264      2.833213
0       0       0.13648433      2.833213
29      1       0.23952033      2.833213
15      2       0.32110173      2.833213
2       3       0.33712     2.833213
0       4       0.34053264      2.833213
0       0       0.13648433      2.833213
19      1       0.23952033      2.833213
25      2       0.32110173      2.833213
3       3       0.33712     2.833213
1       4       0.34053264      2.833213
0       0       0.13648433      2.833213
24      1       0.23952033      2.833213
40      2       0.32110173      2.833213
6       3       0.33712     2.833213
1       4       0.34053264      2.833213
0       0       0.03678637      2.772589
28      1       0.07414634      2.772589
28      2       0.13648433      2.772589
3       3       0.23952033      2.772589
2       4       0.32110173      2.772589
0       0       0.03678637      2.772589
3       1       0.07414634      2.772589
2       2       0.13648433      2.772589
0       3       0.23952033      2.772589
0       4       0.32110173      2.772589
4       0       0.03678637      2.772589
14      1       0.07414634      2.772589
6       2       0.13648433      2.772589
0       3       0.23952033      2.772589
0       4       0.32110173      2.772589
0       0       0.03678637      2.772589
6       1       0.07414634      2.772589
3       2       0.13648433      2.772589
2       3       0.23952033      2.772589
0       4       0.32110173      2.772589
0       0       0.03678637      2.772589
8       1       0.07414634      2.772589
2       2       0.13648433      2.772589
4       3       0.23952033      2.772589
1       4       0.32110173      2.772589
1       0       0.03678637      2.772589
12      1       0.07414634      2.772589
23      2       0.13648433      2.772589
0       3       0.23952033      2.772589
0       4       0.32110173      2.772589
0       0       0.03678637      2.772589
24      1       0.07414634      2.772589
56      2       0.13648433      2.772589
7       3       0.23952033      2.772589
4       4       0.32110173      2.772589
0       0       0.03678637      2.772589
22      1       0.07414634      2.772589
45      2       0.13648433      2.772589
3       3       0.23952033      2.772589
0       4       0.32110173      2.772589
0       0       0.03678637      2.772589
2       1       0.07414634      2.772589
18      2       0.13648433      2.772589
1       3       0.23952033      2.772589
0       4       0.32110173      2.772589
0       0       0.03678637      2.772589
5       1       0.07414634      2.772589
18      2       0.13648433      2.772589
5       3       0.23952033      2.772589
1       4       0.32110173      2.772589
0       0       0.03678637      2.772589
9       1       0.07414634      2.772589
25      2       0.13648433      2.772589
6       3       0.23952033      2.772589
1       4       0.32110173      2.772589
0       0       0.03678637      2.772589
1       1       0.07414634      2.772589
3       2       0.13648433      2.772589
1       3       0.23952033      2.772589
1       4       0.32110173      2.772589
0       0       0.03678637      2.772589
3       1       0.07414634      2.772589
16      2       0.13648433      2.772589
0       3       0.23952033      2.772589
0       4       0.32110173      2.772589
0       0       0.03678637      2.772589
7       1       0.07414634      2.772589
21      2       0.13648433      2.772589
8       3       0.23952033      2.772589
0       4       0.32110173      2.772589
0       0       0.03678637      2.772589
5       1       0.07414634      2.772589
22      2       0.13648433      2.772589
6       3       0.23952033      2.772589
0       4       0.32110173      2.772589
0       0       0.03678637      2.772589
11      1       0.07414634      2.772589
22      2       0.13648433      2.772589
6       3       0.23952033      2.772589
0       4       0.32110173      2.772589
1       0       0.11532605      2.564949
7       1       0.05628636      2.564949
11      2       0.03678637      2.564949
0       3       0.07414634      2.564949
0       4       0.13648433      2.564949
0       0       0.11532605      2.564949
4       1       0.05628636      2.564949
4       2       0.03678637      2.564949
0       3       0.07414634      2.564949
0       4       0.13648433      2.564949
0       0       0.11532605      2.564949
0       1       0.05628636      2.564949
5       2       0.03678637      2.564949
0       3       0.07414634      2.564949
1       4       0.13648433      2.564949
0       0       0.11532605      2.564949
3       1       0.05628636      2.564949
4       2       0.03678637      2.564949
0       3       0.07414634      2.564949
0       4       0.13648433      2.564949
0       0       0.11532605      2.564949
3       1       0.05628636      2.564949
0       2       0.03678637      2.564949
1       3       0.07414634      2.564949
0       4       0.13648433      2.564949
0       0       0.11532605      2.564949
1       1       0.05628636      2.564949
0       2       0.03678637      2.564949
0       3       0.07414634      2.564949
0       4       0.13648433      2.564949
0       0       0.11532605      2.564949
6       1       0.05628636      2.564949
9       2       0.03678637      2.564949
3       3       0.07414634      2.564949
0       4       0.13648433      2.564949
0       0       0.11532605      2.564949
3       1       0.05628636      2.564949
4       2       0.03678637      2.564949
3       3       0.07414634      2.564949
1       4       0.13648433      2.564949
0       0       0.11532605      2.564949
1       1       0.05628636      2.564949
3       2       0.03678637      2.564949
4       3       0.07414634      2.564949
0       4       0.13648433      2.564949
1       0       0.11532605      2.564949
3       1       0.05628636      2.564949
10      2       0.03678637      2.564949
2       3       0.07414634      2.564949
1       4       0.13648433      2.564949
0       0       0.11532605      2.564949
0       1       0.05628636      2.564949
3       2       0.03678637      2.564949
3       3       0.07414634      2.564949
1       4       0.13648433      2.564949
0       0       0.11532605      2.564949
24      1       0.05628636      2.564949
43      2       0.03678637      2.564949
11      3       0.07414634      2.564949
3       4       0.13648433      2.564949
0       0       0.11532605      2.564949
3       1       0.05628636      2.564949
19      2       0.03678637      2.564949
14      3       0.07414634      2.564949
2       4       0.13648433      2.564949
0       0       0.09016875      NA
25      1       0.14227471      2.833213
2       2       0.11532605      2.833213
0       3       0.05628636      2.833213
0       4       0.03678637      2.833213
0       0       0.09016875      2.833213
14      1       0.14227471      2.833213
0       2       0.11532605      2.833213
0       3       0.05628636      2.833213
0       4       0.03678637      2.833213
0       0       0.09016875      2.833213
12      1       0.14227471      2.833213
4       2       0.11532605      2.833213
0       3       0.05628636      2.833213
0       4       0.03678637      2.833213
1       0       0.09016875      2.833213
42      1       0.14227471      2.833213
20      2       0.11532605      2.833213
1       3       0.05628636      2.833213
2       4       0.03678637      2.833213
0       0       0.09016875      2.833213
48      1       0.14227471      2.833213
40      2       0.11532605      2.833213
1       3       0.05628636      2.833213
0       4       0.03678637      2.833213
10      0       0.09016875      2.833213
23      2       0.11532605      2.833213
0       3       0.05628636      2.833213
2       4       0.03678637      2.833213
2       0       0.09016875      2.833213
89      1       0.14227471      2.833213
5       2       0.11532605      2.833213
1       3       0.05628636      2.833213
6       4       0.03678637      2.833213
0       0       0.09016875      2.833213
27      1       0.14227471      2.833213
9       2       0.11532605      2.833213
3       3       0.05628636      2.833213
2       4       0.03678637      2.833213
1       0       0.09016875      2.833213
6       1       0.14227471      2.833213
0       2       0.11532605      2.833213
1       3       0.05628636      2.833213
0       4       0.03678637      2.833213
0       0       0.09016875      2.833213
65      1       0.14227471      2.833213
35      2       0.11532605      2.833213
1       3       0.05628636      2.833213
2       4       0.03678637      2.833213
0       0       0.09016875      2.833213
29      1       0.14227471      2.833213
26      2       0.11532605      2.833213
3       3       0.05628636      2.833213
1       4       0.03678637      2.833213
4       0       0.09016875      2.833213
105     1       0.14227471      2.833213
5       2       0.11532605      2.833213
0       3       0.05628636      2.833213
1       4       0.03678637      2.833213
4       0       0.09016875      2.833213
107     1       0.14227471      2.833213
5       2       0.11532605      2.833213
0       3       0.05628636      2.833213
0       4       0.03678637      2.833213
0       0       0.09016875      2.833213
17      1       0.14227471      2.833213
1       2       0.11532605      2.833213
0       3       0.05628636      2.833213
0       4       0.03678637      2.833213
3       0       0.09016875      2.833213
106     1       0.14227471      2.833213
1       2       0.11532605      2.833213
1       3       0.05628636      2.833213
0       4       0.03678637      2.833213
0       0       0.09016875      2.833213
21      1       0.14227471      2.833213
14      2       0.11532605      2.833213
5       3       0.05628636      2.833213
1       4       0.03678637      2.833213
0       0       0.09016875      2.833213
35      1       0.14227471      2.833213
12      2       0.11532605      2.833213
8       3       0.05628636      2.833213
2       4       0.03678637      2.833213
4       0       0.13510174      1.791759
1       1       0.10188844      1.791759
4       2       0.09016875      1.791759
0       3       0.14227471      1.791759
0       4       0.11532605      1.791759
3       0       0.13510174      1.791759
16      1       0.10188844      1.791759
11      2       0.09016875      1.791759
0       3       0.14227471      1.791759
0       4       0.11532605      1.791759
4       0       0.13510174      1.791759
20      1       0.10188844      1.791759
7       2       0.09016875      1.791759
0       3       0.14227471      1.791759
0       4       0.11532605      1.791759
0       0       0.13510174      1.791759
3       1       0.10188844      1.791759
1       2       0.09016875      1.791759
1       3       0.14227471      1.791759
1       4       0.11532605      1.791759
0       0       0.13510174      1.791759
2       1       0.10188844      1.791759
8       2       0.09016875      1.791759
2       3       0.14227471      1.791759
1       4       0.11532605      1.791759
0       0       0.13510174      1.791759
1       1       0.10188844      1.791759
40      2       0.09016875      1.791759
8       3       0.14227471      1.791759
0       4       0.11532605      1.791759
0       0       0.33638851      2.70805
0       1       0.20354567      2.70805
18      2       0.13510174      2.70805
2       3       0.10188844      2.70805
0       4       0.09016875      2.70805
0       0       0.33638851      2.70805
0       1       0.20354567      2.70805
1       2       0.13510174      2.70805
0       3       0.10188844      2.70805
0       4       0.09016875      2.70805
0       0       0.33638851      2.70805
1       1       0.20354567      2.70805
1       2       0.13510174      2.70805
0       3       0.10188844      2.70805
0       4       0.09016875      2.70805
0       0       0.33638851      2.70805
13      1       0.20354567      2.70805
23      2       0.13510174      2.70805
1       3       0.10188844      2.70805
13      4       0.09016875      2.70805
0       0       0.33638851      2.70805
1       1       0.20354567      2.70805
8       2       0.13510174      2.70805
3       3       0.10188844      2.70805
4       4       0.09016875      2.70805
0       0       0.33638851      2.70805
2       1       0.20354567      2.70805
9       2       0.13510174      2.70805
2       3       0.10188844      2.70805
0       4       0.09016875      2.70805
26      0       0.33638851      2.70805
2       1       0.20354567      2.70805
2       2       0.13510174      2.70805
0       3       0.10188844      2.70805
0       4       0.09016875      2.70805
57      0       0.33638851      2.70805
4       1       0.20354567      2.70805
6       2       0.13510174      2.70805
0       3       0.10188844      2.70805
1       4       0.09016875      2.70805
26      0       0.33638851      2.70805
3       1       0.20354567      2.70805
10      2       0.13510174      2.70805
2       3       0.10188844      2.70805
3       4       0.09016875      2.70805
9       0       0.33638851      2.70805
1       1       0.20354567      2.70805
3       2       0.13510174      2.70805
2       3       0.10188844      2.70805
0       4       0.09016875      2.70805
0       0       0.33638851      2.70805
0       1       0.20354567      2.70805
6       2       0.13510174      2.70805
1       3       0.10188844      2.70805
0       4       0.09016875      2.70805
0       0       0.33638851      2.70805
4       1       0.20354567      2.70805
16      2       0.13510174      2.70805
12      3       0.10188844      2.70805
3       4       0.09016875      2.70805
0       0       0.33638851      2.70805
7       1       0.20354567      2.70805
19      2       0.13510174      2.70805
8       3       0.10188844      2.70805
2       4       0.09016875      2.70805
14      0       0.33638851      2.70805
8       1       0.20354567      2.70805
33      2       0.13510174      2.70805
25      3       0.10188844      2.70805
4       4       0.09016875      2.70805
5       1       0.20354567      2.70805
15      2       0.13510174      2.70805
20      3       0.10188844      2.70805
10      4       0.09016875      2.70805
8       0       0.17597738      2.833213
28      1       0.25832942      2.833213
6       2       0.33638851      2.833213
0       3       0.20354567      2.833213
0       4       0.13510174      2.833213
4       0       0.17597738      2.833213
15      1       0.25832942      2.833213
27      2       0.33638851      2.833213
0       3       0.20354567      2.833213
0       4       0.13510174      2.833213
5       0       0.17597738      2.833213
13      1       0.25832942      2.833213
6       2       0.33638851      2.833213
0       3       0.20354567      2.833213
1       4       0.13510174      2.833213
0       0       0.17597738      2.833213
1       1       0.25832942      2.833213
0       2       0.33638851      2.833213
0       3       0.20354567      2.833213
2       4       0.13510174      2.833213
0       0       0.17597738      2.833213
6       1       0.25832942      2.833213
22      2       0.33638851      2.833213
0       3       0.20354567      2.833213
0       4       0.13510174      2.833213
0       0       0.17597738      2.833213
0       1       0.25832942      2.833213
11      2       0.33638851      2.833213
1       3       0.20354567      2.833213
2       4       0.13510174      2.833213
2       0       0.17597738      2.833213
0       1       0.25832942      2.833213
7       2       0.33638851      2.833213
3       3       0.20354567      2.833213
0       4       0.13510174      2.833213
1       0       0.17597738      2.833213
14      1       0.25832942      2.833213
23      2       0.33638851      2.833213
0       3       0.20354567      2.833213
1       4       0.13510174      2.833213
0       0       0.17597738      2.833213
0       1       0.25832942      2.833213
5       2       0.33638851      2.833213
2       3       0.20354567      2.833213
0       4       0.13510174      2.833213
0       0       0.17597738      2.833213
3       1       0.25832942      2.833213
6       2       0.33638851      2.833213
0       3       0.20354567      2.833213
1       4       0.13510174      2.833213
0       0       0.17597738      2.833213
0       1       0.25832942      2.833213
2       2       0.33638851      2.833213
0       3       0.20354567      2.833213
4       4       0.13510174      2.833213
2       0       0.17597738      2.833213
39      1       0.25832942      2.833213
18      2       0.33638851      2.833213
7       3       0.20354567      2.833213
0       4       0.13510174      2.833213
3       0       0.17597738      2.833213
25      1       0.25832942      2.833213
9       2       0.33638851      2.833213
3       3       0.20354567      2.833213
0       4       0.13510174      2.833213
4       0       0.17597738      2.833213
7       1       0.25832942      2.833213
1       2       0.33638851      2.833213
1       3       0.20354567      2.833213
0       4       0.13510174      2.833213
0       0       0.17597738      2.833213
1       1       0.25832942      2.833213
6       2       0.33638851      2.833213
1       3       0.20354567      2.833213
0       4       0.13510174      2.833213
2       0       0.17597738      2.833213
15      1       0.25832942      2.833213
49      2       0.33638851      2.833213
19      3       0.20354567      2.833213
2       4       0.13510174      2.833213
0       0       0.17597738      2.833213
0       1       0.25832942      2.833213
1       2       0.33638851      2.833213
0       3       0.20354567      2.833213
0       4       0.13510174      2.833213
3       0       0.17485677      2.302585
50      1       0.17597738      2.302585
25      2       0.25832942      2.302585
0       3       0.33638851      2.302585
0       4       0.20354567      2.302585
1       0       0.17485677      2.302585
7       1       0.17597738      2.302585
8       2       0.25832942      2.302585
0       3       0.33638851      2.302585
0       4       0.20354567      2.302585
3       0       0.17485677      2.302585
16      1       0.17597738      2.302585
63      2       0.25832942      2.302585
3       3       0.33638851      2.302585
0       4       0.20354567      2.302585
1       0       0.17485677      2.302585
34      1       0.17597738      2.302585
12      3       0.33638851      2.302585
4       4       0.20354567      2.302585
0       0       0.17485677      2.302585
29      1       0.17597738      2.302585
16      2       0.25832942      2.302585
0       3       0.33638851      2.302585
0       4       0.20354567      2.302585
0       0       0.17485677      2.302585
30      1       0.17597738      2.302585
13      2       0.25832942      2.302585
0       3       0.33638851      2.302585
2       4       0.20354567      2.302585
0       0       0.17485677      2.302585
15      1       0.17597738      2.302585
10      2       0.25832942      2.302585
0       3       0.33638851      2.302585
1       4       0.20354567      2.302585
4       0       0.17485677      2.302585
50      1       0.17597738      2.302585
32      2       0.25832942      2.302585
6       3       0.33638851      2.302585
8       4       0.20354567      2.302585
0       0       0.17485677      2.302585
32      1       0.17597738      2.302585
29      2       0.25832942      2.302585
4       3       0.33638851      2.302585
8       4       0.20354567      2.302585
0       0       0.17485677      2.302585
2       1       0.17597738      2.302585
2       2       0.25832942      2.302585
2       3       0.33638851      2.302585
3       4       0.20354567      2.302585

Dmso

Answer 1

For visualizing the goodness of fit of probabilistic regression models, "standard" residuals (e.g., Poisson or deviance) are often not so informative because they mostly capture the modeling of the mean but not of the entire distribution. One alternative that is somtimes used are (randomized) quantile residuals. Without randomization they are defined as qnorm(pdist(y)) where pdist() is the fitted distribution function (here a ZIP model), y are the observations, and qnorm() is the quantile function of the standard normal distribution. If the model fits, the distribution of the residuals should be standard normal and can be checked in a Q-Q plot. In case of discrete distributions (as here), randomization is needed to break up the discrete nature of the data. See Dunn & Smyth (1996, Journal of Computational and Graphical Statistics, 5, 236-244) for more details. In R you can use the countreg package from R-Forge (hopefully soon also on CRAN) for these.

Another alternative which checks the marginal distribution of the data is the so-called rootogram. It visually compares the observed and fitted frequencies for the counts, 0, 1, ... It is often better at displaying the problems of excess zeros and/or overdispersion than Q-Q plots of randomized quantile residuals. See our paper Kleiber & Zeileis (2016, The American Statistician, 70(3), 296–303, doi:10.1080/00031305.2016.1173590) for more details.

Applying these to your regression model quickly shows that a zero-inflated Poisson is not accounting for the overdispersion in the response. (With counts up to and beyond 100 a Poisson-based distribution almost never fits well.) Furthermore, a zero inflation model does not fit very well because for assnage = 1 and = 2 there are very few zeros and no zero inflation is needed. This leads to corresponding coefficients in the zero inflation part that go towards -Inf with very large standard errors (like in quasi-separation in binary regression). Therefore, a two-part hurdle model fits somewhat better and is likely easier to interpret. Finally, due to the two assnage groups being different I would code assnage as a factor (it is not clear to me whether you did that already).

Thus, for analyzing your data I use yc as provided in your post and ensure:

yc$assnage <- factor(yc$assnage)

For a first explorative look at the influence of assnage I plot whether or not the count is positive (left: zero hurdle) and the positive count on a log-scale (right: count).

plot(factor(count > 0, levels = c(FALSE, TRUE), labels = c("=0", ">0")) ~ assnage,
  data = yc, ylab = "count", main = "Zero hurdle")
plot(count ~ assnage, data = yc, subset = count > 0,
  log = "y", main = "Count (positive)")

Then, I fit the ZIP, ZINB, and hurdle NB models using the countreg package from R-Forge. This also contains updated versions of the zeroinfl() and hurdle() functions.

install.packages("countreg", repos = "http://R-Forge.R-project.org")
library("countreg")
zip <- zeroinfl(count ~ assnage * spawncob, offset = logoffset,
  data = yc, dist = "poisson")
zinb <- zeroinfl(count ~ assnage * spawncob, offset = logoffset,
  data = yc, dist = "negbin")
hnb <- hurdle(count ~ assnage * spawncob, offset = logoffset, data = yc,
  dist = "negbin")

The ZIP is clearly inappropriate and the hurdle NB is slightly better than the ZINB.

BIC(zip, zinb, hnb)
##      df      BIC
## zip  20 7700.085
## zinb 21 3574.720
## hnb  21 3556.693

If you check summary(zinb) you will also see that some coefficients in the zero-inflation part are around 10 (for a dummy variable) with standard errors one or two orders of magnitude larger. This essentially means that the zero-inflation probability in the corresponding groups goes to zero because the negative binomial distribution already has more than enough probability weight for the zero responses (assnage groups 1 and 2).

To visualize that the ZIP model does not fit while the HNB appropriately captures the response, we can now use the rootograms.

rootogram(zip, main = "ZIP", ylim = c(-5, 15), max = 50)
rootogram(hnb, main = "HNB", ylim = c(-5, 15), max = 50)

The wave-like pattern for the ZIP clearly shows the overdispersion in the data that is not appropriately captured by the model. In contrast, the hurdle fits reasonably well.

As a final check we can also look at the Q-Q plot of the quantile residuals in the hurdle model. These look fairly normal and show no suspicious departures from the model.

qqrplot(hnb, main = "HNB")

As the residuals are randomized, you can re-run the code a couple of times to get an impression of the variation. qqrplot() has also some arguments that let's you explore this variation in a single plot.

Maggi

I appreciate your thorough answer and it has really helped me explore the "fit" if zero-inflated models. Can you elaborate on using rootogram() and qqrplot()? I am running the code in the same manner as you but run into errors such as: **************Error in rootogram.default(zintfd) : argument "fitted" is missing, with no default******************** and I'm having a hard time finding the function or package that includes qqrplot(). – Dmso

I guess that you have used the rootogram() function from the vcd package. This is another implementation of rootograms but not suitable for regression models. As indicated in my answer above, you need to install the countreg package from R-Forge. This contains everything you need: improved versions of the regression models zeroinfl(), hurdle() as well as the diagnostic plots rootogram() and qqrplot(). – Maggi

I was using the incorrect packages. Thank you for clarifying! – Dmso