Linear Programing- Max value optimization

Question

I'm trying to find the best possible combination that will maximize my sum value, but it has to be under 2 specific constraints, therefore I am assuming Linear programming will be the best fit.

The problem goes like this: Some educational world-event wish to gather the world's smartest teen students. Every state tested 100K students on the following exams:'MATH', 'ENGLISH', 'COMPUTERS', 'HISTORY','PHYSICS'.. and where graded 0-100 on EACH exam.

Every state was requested to send their best 10K from the tested 100K students for the event.

You, as the French representative, were requested to choose the top 10K students from the tested 100K student from your country. For that, you'll need to optimize the MAX VALUE from them in order to get the best possible TOTAL SCORE.

BUT there are 2 main constrains:

1- from the total 10K chosen students you need to allocate specific students that will be tested on the event on 1 specific subject only from the mentioned 5 subjects. the allocation needed is: ['MATH': 4000, 'ENGLISH':3000,'COMPUTERS':2000, 'HISTORY':750,'PHYSICS':250]

2- Each 'exam subject' score will have to be weighted differently.. for exp: 97 is Math worth more than 97 in History. the wheights are: ['MATH': 1.9, 'ENGLISH':1.7,'COMPUTERS':1.5, 'HISTORY':1.3,'PHYSICS':1.1]

MY SOLUTION: I tried to use the PULP (python) as an LP library and solved it correctly, but it took more than 2 HOURS of running. can you find a better (faster, simpler..) way to solve it? there are some NUMPY LP functions that could be used instead, maybe will be faster? it supposed to be a simple OPTIMIZATION problem be I made it too slow and complexed. --The solution needs to be in Python only please

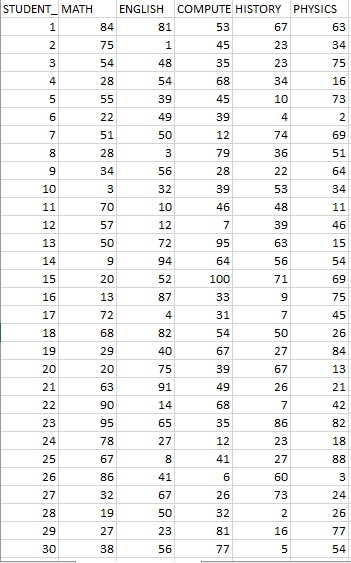
for example, let's look on a small scale at the same problem: there are 30 students and you need to choose only 15 students that will give us the best combination in relation to the following subject allocation demand. the allocation needed is- ['MATH': 5, 'ENGLISH':4,'COMPUTERS':3, 'HISTORY':2,'PHYSICS':1]

this is all the 30 students and their grades:

after running the algorithm, the output solution will be:

here is my full code for the ORIGINAL question (100K students):

import pandas as pd
import numpy as np
import pulp as p
import time    
t0=time.time()

demand = [4000, 3000, 2000, 750,250]
weight = [1.9,1.7, 1.5, 1.3, 1.1]


original_data= pd.read_csv('GRADE_100K.csv') #created simple csv file with random scores
data_c=original_data.copy()
data_c.index = np.arange(1, len(data_c)+1)
data_c.columns
data_c=data_c[['STUDENT_ID', 'MATH', 'ENGLISH', 'COMPUTERS', 'HISTORY','PHYSICS']]

#DataFrame Shape
m=data_c.shape[1]
n=data_c.shape[0]

data=[]
sublist=[]
for j in range(0,n):
    for i in range(1,m):
        sublist.append(data_c.iloc[j,i])
    data.append(sublist)
    sublist=[]


def _get_num_students(data):
    return len(data)


def _get_num_subjects(data):
    return len(data[0])


def _get_weighted_data(data, weight):
    return [
        [a*b for a, b in zip(row, weight)]
        for row in data
    ]



data = _get_weighted_data(data, weight)
num_students = _get_num_students(data)
num_subjects = _get_num_subjects(data)

# Create a LP Minimization problem
Lp_prob = p.LpProblem('Problem', p.LpMaximize)

# Create problem Variables
variables_matrix = [[0 for i in range(num_subjects)] for j in range(num_students)]
for i in range(0, num_students):
    for j in range(0, num_subjects):
        variables_matrix[i][j] = p.LpVariable(f"X({i+1},{j+1})", 0, 1, cat='Integer')


df_d=pd.DataFrame(data=data)
df_v=pd.DataFrame(data=variables_matrix)

ml=df_d.mul(df_v)

ml['coeff'] = ml.sum(axis=1)

coefficients=ml['coeff'].tolist()


# DEALING WITH TARGET FUNCTION VALUE

suming=0
k=0
sumsum=[]
for z in range(len(coefficients)):
    suming +=coefficients[z] 
    if z % 2000==0:
        sumsum.append(suming) 
        suming=0
if z<2000:
    sumsum.append(suming) 

sumsuming=0
for s in range(len(sumsum)):
    sumsuming=sumsuming+sumsum[s]        

Lp_prob += sumsuming   



# DEALING WITH the 2 CONSTRAINS

# 1-subject constraints

con1_suming=0
for e in range(num_subjects):
    L=df_v.iloc[:,e].to_list() 
    for t in range(len(L)):
        con1_suming +=L[t]
    Lp_prob += con1_suming <= demand[e] 
    con1_suming=0 


 # 2- students constraints

con2_suming=0
for e in range(num_students):
    L=df_v.iloc[e,:].to_list() 
    for t in range(len(L)):
        con2_suming +=L[t]
    Lp_prob += con2_suming <= 1 
    con2_suming=0        
print("time taken for TARGET+CONSTRAINS %8.8f seconds" % (time.time()-t0) )


t1=time.time()

status = Lp_prob.solve()  # Solver
print("time taken for SOLVER %8.8f seconds" % (time.time()-t1) )  # 632 SECONDS
print(p.LpStatus[status])  # The solution status
print(p.value(Lp_prob.objective))



df_v=pd.DataFrame(data=variables_matrix)


# Printing the final solution
lst=[]
val=[]

for i in range(0, num_students):
    lst.append([p.value(variables_matrix[i][j]) for j in range(0, num_subjects)])
    val.append([sum([p.value(variables_matrix[i][j]) for j in range(0, num_subjects)]),i])


ones_places=[]
for i in range (0, len(val)):
    if val[i][0]==1:
        ones_places.append(i+1)       
len(ones_places)  


data_once=data_c[data_c['STUDENT_ID'].isin(ones_places)]

IDs=[]
for i in range(len(ones_places)):
    IDs.append(data_once['STUDENT_ID'].to_list()[i])

course=[]
sub_course=[]
for i in range(len(lst)):
    j=0
    sub_course='x'
    while j<len(lst[i]):
        if lst[i][j]==1:
           sub_course=j 
        j=j+1
    course.append(sub_course)

coures_ones=[]
for i in range(len(course)):
    if course[i]!= 'x':
        coures_ones.append(course[i])     

# adding the COURSE name to the final table
# NUMBER OF DICTIONARY KEYS based on number of COURSES      
col=original_data.columns.values[1:].tolist()   
dic = {0:col[0], 1:col[1], 2:col[2], 3:col[3], 4:col[4]}
cc_name=[dic.get(n, n) for n in coures_ones]
     
one_c=[]
if len(IDs)==len(cc_name):
    for i in range(len(IDs)):
        one_c.append([IDs[i],cc_name[i]])

prob=[] 
if len(IDs)==len(cc_name):
    for i in range(len(IDs)):
        prob.append([IDs[i],cc_name[i], data_once.iloc[i][one_c[i][1]]])

scoring_table = pd.DataFrame(prob,columns=['STUDENT_ID','COURES','SCORE'])
scoring_table.sort_values(by=['COURES', 'SCORE'], ascending=[False, False], inplace=True)
scoring_table.index = np.arange(1, len(scoring_table)+1)


print(scoring_table)

Domitian

Glancing at it, that seems like a lot of values with relatively few constraints, so I'd imagine that it would take a long time regardless of what you did. – Sheave

Hi, thanks! would you suggest diffrent approch then Linear Progrming for it? outer ideas may improve it? – Domitian

It is not clear to me. Do you want as step 1 : take the 10k best students regarding total score over the exams (with sum as summary function) and step 2 : create the best possible groups [4k, 3k, 2k, 1k, 0.5k] (warning here they are duplicates) to maximise the score at each weighted exam for your country ? – Primrose

Hi! it suppose to be done on 1 step.. you should choose 10K students from the 100K and to choose for each with kind of subject to be tested on from the 5 possible subjects. the main goal is choose the best comination of 10K students and fit them with the best possible subjects to be tested on (in relate to the scores they got on the exams..). the best possible combination will maximize the possible score value. – Domitian

I think it is possible to reformulate the problem as a min cost flow problem. As such one would not need integer linear programming and would be in P and not NP. Thus I would assume there should be ways to solve this more efficiently. – Shadshadberry

I have two questions: 1. you say you need 10K students to be tested on only one exam each, but the exam allocations that you list sum to more than 10K. Is that just a typo, or are those exam allocations an upper bound, not a strict equality. 2. What solver PulP using? The problem you've specified is linear, but the solver may get tripped up with the integer constraints. This is really a network/assignment optimization problem so the structure may allow you to solve without the integer constraint and still get integer values if the bounds and coefficients are all integer. – Extramundane

After having thought about the min cost flow formulation I also came to the conclusion that the LP relaxation of this problem should be integral. So @Extramundane idea might be worth considering. Still to my knowledge solving min cost flow is a computationally easier problem than solving an LP. – Shadshadberry

I have just added a python implementation to my answer. It turns out using min cost flow indeed boosts the runtime significantly. I am down to <20s including setup and solution extraction. – Shadshadberry

Using random scores (100k students), a commercial LP solver can solve this in about 5 seconds. – Obsessive

Getting challenged by the 5s mark @ErwinKalvelagen mentioned I modified the solution extraction of my code pushing the total runtime (including the random number generation) to <2s. Without the random number generation and the setup I am down to <1s. See code modifications in my answer. – Shadshadberry

Answer 1

Here are some more ideas on my idea of using min cost flows.

We model this problem by taking a directed graph with 4 layers, where each layer is fully connected to the next.

Nodes

• First layer: A single node s that will be our source.

• Second layer: One node for each student.

• Third layer: One node for each subject.

• Fourth layer: OA single node t that will be our drain.

Edge Capacities

• First -> Second: All edges have capacity 1.

• Second -> Third: All edges have capacity 1.

• Third -> Fourth: All edges have the capacity corresponding to the number students that has to be assigned to that subject.

Edge Costs

• First -> Second: All edges have cost 0.

• Second -> Third: Remember that edges in this layer connect a student with a subject. The costs on these will be chosen anti proportional to the weighted score the student has on that subject. cost = -subject_weight*student_subject_score.

• Third -> Fourth: All edges have cost 0.

Then we demand a flow from s to t equal to the number of students we have to choose.

Why does this work?

A solution to the min cost flow problem will correspond to a solution of your problem by taking all the edges between the third and fourth layer as assignments.

Each student can be chosen for at most one subject, as the corresponding node has only one incoming edge.

Each subject has exactly the number of required students, as the outgoing capacity corresponds to the number of students we have to choose for this subject and we have to use the full capacity of these edges, as we can not fulfil the flow demand otherwise.

A minimal solution to the MCF problem corresponds to the maximal solution of your problem, as the costs corresponds to the value they give.

As you asked for a solution in python I implemented the min cost flow problem with ortools. Finding a solution took less than a second in my colab notebook. What takes "long" is the extraction of the solution. But including setup and solution extraction I am still having a runtime of less than 20s for the full 100000 student problem.

Code

# imports
from ortools.graph import pywrapgraph
import numpy as np
import pandas as pd
import time
t_start = time.time()

# setting given problem parameters
num_students = 100000
subjects = ['MATH', 'ENGLISH', 'COMPUTERS', 'HISTORY','PHYSICS']
num_subjects = len(subjects)
demand = [4000, 3000, 2000, 750, 250]
weight = [1.9,1.7, 1.5, 1.3, 1.1]

# generating student scores
student_scores_raw = np.random.randint(101, size=(num_students, num_subjects))

# setting up graph nodes
source_nodes = [0]
student_nodes = list(range(1, num_students+1))
subject_nodes = list(range(num_students+1, num_subjects+num_students+1))
drain_nodes = [num_students+num_subjects+1]

# setting up the min cost flow edges
start_nodes = [int(c) for c in (source_nodes*num_students + [i for i in student_nodes for _ in subject_nodes] + subject_nodes)]
end_nodes   = [int(c) for c in (student_nodes + subject_nodes*num_students + drain_nodes*num_subjects)]
capacities  = [int(c) for c in ([1]*num_students + [1]*num_students*num_subjects + demand)]
unit_costs  = [int(c) for c in ([0.]*num_students + list((-student_scores_raw*np.array(weight)*10).flatten()) + [0.]*num_subjects)]
assert len(start_nodes) == len(end_nodes) == len(capacities) == len(unit_costs)

# setting up the min cost flow demands
supplies = [sum(demand)] + [0]*(num_students + num_subjects) + [-sum(demand)]

# initialize the min cost flow problem instance
min_cost_flow = pywrapgraph.SimpleMinCostFlow()
for i in range(0, len(start_nodes)):
  min_cost_flow.AddArcWithCapacityAndUnitCost(start_nodes[i], end_nodes[i], capacities[i], unit_costs[i])
for i in range(0, len(supplies)):
  min_cost_flow.SetNodeSupply(i, supplies[i])

# solve the problem
t_solver_start = time.time()
if min_cost_flow.Solve() == min_cost_flow.OPTIMAL:
  print('Best Value:', -min_cost_flow.OptimalCost()/10)
  print('Solver time:', str(time.time()-t_solver_start)+'s')
  print('Total Runtime until solution:', str(time.time()-t_start)+'s')
  
  #extracting the solution
  solution = []
  for i in range(min_cost_flow.NumArcs()):
    if min_cost_flow.Flow(i) > 0 and min_cost_flow.Tail(i) in student_nodes:
      student_id = min_cost_flow.Tail(i)-1
      subject_id = min_cost_flow.Head(i)-1-num_students
      solution.append([student_id, subjects[subject_id], student_scores_raw[student_id, subject_id]])
  assert(len(solution) == sum(demand))

  solution = pd.DataFrame(solution, columns = ['student_id', 'subject', 'score'])
  print(solution.head())
else:
  print('There was an issue with the min cost flow input.')

print('Total Runtime:', str(time.time()-t_start)+'s')

Replacing the for-loop for the solution extraction in the above code by the following list-comprehension (that is not also not using list lookups every iteration) the runtime can be improved significantly. But for readability reasons I will leave this old solution here as well. Here is the new one:

  solution = [[min_cost_flow.Tail(i)-1, 
               subjects[min_cost_flow.Head(i)-1-num_students], 
               student_scores_raw[min_cost_flow.Tail(i)-1, min_cost_flow.Head(i)-1-num_students]
               ]
              for i in range(min_cost_flow.NumArcs())
              if (min_cost_flow.Flow(i) > 0 and 
                  min_cost_flow.Tail(i) <= num_students and 
                  min_cost_flow.Tail(i)>0)
              ]

The following output is giving the runtimes for the new faster implementation.

Output

Best Value: 1675250.7
Solver time: 0.542395830154419s
Total Runtime until solution: 1.4248979091644287s
   student_id    subject  score
0           3    ENGLISH     99
1           5       MATH     98
2          17  COMPUTERS    100
3          22  COMPUTERS    100
4          33    ENGLISH    100
Total Runtime: 1.752336025238037s

Pleas point out any mistakes I might have made.

I hope this helps. ;)

Shadshadberry

I don't think this is a valid approach. Among other problems, it does not appear to have the capability to constrain a student node from being connected to multiple tests. – Broncobuster

The capacity between the first two layers bounds a student from having more than one incoming flow. Thus, by flow conservation they also have at most one outgoing flow - prevention it to be connected to multiple subjects. – Shadshadberry

Answer 2

I think you're close on this. It is a fairly standard Integer Linear Program (ILP) assignment problem. It's gonna be a bit slow because of the structure of the problem.

You didn't say in your post what the breakdown of the setup & solve times were. I see you are reading from a file and using pandas. I think pandas gets clunky pretty quick with optimization problems, but that is just a personal preference.

I coded your problem up in pyomo, using the cbc solver, which I'm pretty sure is the same one used by pulp for comparison. (see below). I think you have it right with 2 constraints and a dual-indexed binary decision variable.

If I chop it down to 10K students (no slack...just 1-for-1 pairing) it solves in 14sec for comparison. My setup is a 5 year old iMac w/ lots of ram.

Running with 100K students in the pool, it solves in about 25min with 10sec "setup" time before the solver is invoked. So I'm not really sure why your encoding is taking 2hrs. If you can break down your solver time, that would help. The rest should be trivial. I didn't poke around too much in the output, but the OBJ function value of 980K seems reasonable.

Other ideas:

If you can get the solver options to configure properly and set a mip gap of 0.05 or so, it should speed things way up, if you can accept a slightly non-optimal solution. I've only had decent luck with solver options with the paid-for solvers like Gurobi. I haven't had much luck with that using the freebie solvers, YMMV.

import pyomo.environ as pyo
from random import randint
from time import time

# start setup clock
tic = time()
# exam types
subjects = ['Math', 'English', 'Computers', 'History', 'Physics']

# make set of students...
num_students = 100_000
students = [f'student_{s}' for s in range(num_students)]

# make 100K fake scores in "flat" format
student_scores = { (student, subj) : randint(0,100) 
                        for student in students
                        for subj in subjects}

assignments = { 'Math': 4000, 'English': 3000, 'Computers': 2000, 'History': 750, 'Physics': 250}
weights = {'Math': 1.9, 'English': 1.7, 'Computers': 1.5, 'History': 1.3, 'Physics': 1.1}

# Set up model
m = pyo.ConcreteModel('exam assignments')

# Sets
m.subjects = pyo.Set(initialize=subjects)
m.students = pyo.Set(initialize=students)

# Parameters
m.assignments = pyo.Param(m.subjects, initialize=assignments)
m.weights =     pyo.Param(m.subjects, initialize=weights)
m.scores =      pyo.Param(m.students, m.subjects, initialize=student_scores)

# Variables
m.x = pyo.Var(m.students, m.subjects, within=pyo.Binary)  # binary selection of pairing student to test

# Objective
m.OBJ = pyo.Objective(expr=sum(m.scores[student, subject] * m.x[student, subject] 
                for student in m.students
                for subject in m.subjects), sense=pyo.maximize)

### Constraints ###
# fill all assignments
def fill_assignments(m, subject):
    return sum(m.x[student, subject] for student in m.students) == assignments[subject]
m.C1 = pyo.Constraint(m.subjects, rule=fill_assignments)

# use each student at most 1 time
def limit_student(m, student):
    return sum(m.x[student, subject] for subject in m.subjects) <= 1
m.C2 = pyo.Constraint(m.students, rule=limit_student)

toc = time()
print (f'setup time: {toc-tic:0.3f}')
tic = toc

# solve it..
solver = pyo.SolverFactory('cbc')
solution = solver.solve(m)
print(solution)
toc = time()
print (f'solve time: {toc-tic:0.3f}')

Output

setup time: 10.835

Problem: 
- Name: unknown
  Lower bound: -989790.0
  Upper bound: -989790.0
  Number of objectives: 1
  Number of constraints: 100005
  Number of variables: 500000
  Number of binary variables: 500000
  Number of integer variables: 500000
  Number of nonzeros: 495094
  Sense: maximize
Solver: 
- Status: ok
  User time: -1.0
  System time: 1521.55
  Wallclock time: 1533.36
  Termination condition: optimal
  Termination message: Model was solved to optimality (subject to tolerances), and an optimal solution is available.
  Statistics: 
    Branch and bound: 
      Number of bounded subproblems: 0
      Number of created subproblems: 0
    Black box: 
      Number of iterations: 0
  Error rc: 0
  Time: 1533.8383190631866
Solution: 
- number of solutions: 0
  number of solutions displayed: 0

solve time: 1550.528

Broncobuster

I don't think a mip gap will help with this model as it is basically an LP and not a MIP (assignment problems deliver integer solutions automatically), – Obsessive

Good point. I hadn't thought about that angle. With same construct and change to real valued decision variables, I get solve time down by quite a bit to about 450sec – Broncobuster

number of solutions: 0 That must be a bug. – Obsessive