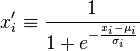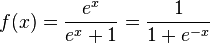Different Sigmoid Equations and its implementation

Question

When reviewing through the Sigmoid function that is used in Neural Nets, we found this equation from https://en.wikipedia.org/wiki/Softmax_function#Softmax_Normalization:

Different from the standard sigmoid equation:

The first equation on top somehow involves the mean and standard deviation (I hope I didn't read the symbols wrongly) whereas the 2nd equation generalized the minus mean and divided by standard deviation as a constant since it's the same throughout all terms within a vector/matrix/tensor.

So when implementing the equations, I get different results.

With the 2nd equation (standard sigmoid function):

def sigmoid(x):
    return 1. / (1 + np.exp(-x))

I get these output:

>>> x = np.array([1,2,3])
>>> print sigmoid(x)
[ 0.73105858  0.88079708  0.95257413]

I would have expect the 1st function to be the similar but the gap between the first and second element widens by quite a bit (though the ranking of the elements remains:

def get_statistics(x):
    n = float(len(x))
    m = x.sum() / n
    s2 = sum((x - m)**2) / (n-1.) 
    s = s2**0.5
    return m, s2, s

m, s, s2 = get_statistics(x)

sigmoid_x1 = 1 / (1 + np.exp(-(x[0] - m) / s2))
sigmoid_x2 = 1 / (1 + np.exp(-(x[1] - m) / s2))
sigmoid_x3 = 1 / (1 + np.exp(-(x[2] - m) / s2))
sigmoid_x1, sigmoid_x2, sigmoid_x3 

[out]:

(0.2689414213699951, 0.5, 0.7310585786300049)

Possibly it has to do with the fact that the first equation contains some sort of softmax normalization but if it's generic softmax then the elements need to sum to one as such:

def softmax(x):
    exp_x = np.exp(x)
    return exp_x / exp_x.sum()

[out]:

>>> x = np.array([1,2,3])
>>> print softmax(x)
[ 0.09003057  0.24472847  0.66524096]

But the output from the first equation don't sum to one and it isn't similar/same as the standard sigmoid equation. So the question is:

• Have I implemented the function for equation 1 wrongly?
• Is equation 1 on the wikipedia page wrong? Or is it referring to something else and not really the sigmoid/logistic function?
• Why is there a difference in the first and second equation?

Pall

Edited my answer, hope this example helps. – Ilo

Why did you add a bounty? What's missing for you to accept my or Marcins answer? – Ilo

It's to get more answers or explanations from different perspectives. Don't worry your answer should be winning the checkmark and/or the bounty. Unless someone comes up with an even more stellar answer ;P – Pall

Answer 1

You have implemented the equations correctly. Your problem is that you are mixing up the definitions of softmax and sigmoid functions.

A softmax function is a way to normalize your data by making outliers "less interesting". Additionally, it "squashes" your input vector in a way that it ensures the sum of the vector to be 1.

For your example:

> np.sum([ 0.09003057,  0.24472847,  0.66524096])
> 1.0

It is simply a generalization of a logistic function with the additional "constraint" to get every element of the vector in the interval (0, 1) and its sum to 1.0.

The sigmoid function is another special case of logistic functions. It is just a real-valued, differentiable function with a bell shape. It is interesting for neural networks because it is rather easy to compute, non-linear and has negative and positive boundaries, so your activation can not diverge but runs into saturation if it gets "too high".

However, a sigmoid function is not ensuring that an input vector sums up to 1.0.

In neural networks, sigmoid functions are used frequently as an activation function for single neurons, while a sigmoid/softmax normalization function is rather used at the output layer, to ensure the whole layer adds up to 1. You just mixed up the sigmoid function (for single neurons) versus the sigmoid/softmax normalization functions (for a whole layer).

EDIT: To clearify this for you I will give you an easy example with outliers, this demonstrates the behaviour of the two different functions for you.

Let's implement a sigmoid function:

import numpy as np

def s(x):
    return 1.0 / (1.0 + np.exp(-x))

And the normalized version (in little steps, making it easier to read):

def sn(x):
    numerator = x - np.mean(x)
    denominator = np.std(x)
    fraction = numerator / denominator

    return 1.0 / (1.0 + np.exp(-fraction))

Now we define some measurements of something with huge outliers:

measure = np.array([0.01, 0.2, 0.5, 0.6, 0.7, 1.0, 2.5, 5.0, 50.0, 5000.0])

Now we take a look at the results that s (sigmoid) and sn (normalized sigmoid) give:

> s(measure)
> array([ 0.50249998,  0.549834  ,  0.62245933,  0.64565631,  0.66818777,
    0.73105858,  0.92414182,  0.99330715,  1.        ,  1.        ])

> sn(measure)
> array([ 0.41634425,  0.41637507,  0.41642373,  0.41643996,  0.41645618,
    0.41650485,  0.41674821,  0.41715391,  0.42447515,  0.9525677 ])

As you can see, s only translates the values "one-by-one" via a logistic function, so the outliers are fully satured with 0.999, 1.0, 1.0. The distance between the other values varies.

When we look at sn we see that the function actually normalized our values. Everything now is extremely identical, except for 0.95 which was the 5000.0.

What is this good for or how to interpret this?

Think of an output layer in a neural network: an activation of 5000.0 in one class on an output layer (compared to our other small values) means that the network is really sure that this is the "right" class to your given input. If you would have used s there, you would end up with 0.99, 1.0 and 1.0 and would not be able to distinguish which class is the correct guess for your input.

Ilo

Thank you, I understand the difference between softmax and sigmoid but why are there 2 equations that are different for sigmoid? – Pall

Just to check with you about your last sentence in the answer, the sigmoid function and sigmoid normalization functions are different? Or are they using the same standard sigmoid function? – Pall

Yes, they are different. The sigmoid function computes 1/(1+e^(-x) for one element at a time while the normalized computes 1/(1+e^(-((x_i ) - mean(x))/std(x)). Hence, the first computes this "single" operation per element in a vector, while the latter always takes the mean and the standard deviation into account. – Ilo

Thanks @ascentor, now the example shows the clear difference! – Pall

Interesting if the sigmoid() non-normalized saturates then wouldn't the boundary be [0,1] instead of (0,1)? Is it saturating because of computational approximation? Or would it really saturate "naturally" – Pall

No, it would not. The denominator is always greater than 1, thus the fraction can not get to exactly 1.0. I would suggest you review mathematics (analysis) for the basics there: e^-(...) is equal to 1/e^(...) and such e-functions just converge to zero, but they never "hit" zero. However, a computer can just represent discrete values, hence, the smaller the distance to zero is, the likelier it is that the computer can not represent this number any more and will simply round it to 1.0. – Ilo

Answer 2

In this case you have to differentiate between three things : a sigmoid function, a sigmoid function with softmax normalization and softmax function.

1. A sigmoid function is a real-valued function which is simpy given by an equation f(x) = 1 / (1 + exp(-x)). For many years it was used in machine learning domain because of the fact that it squashes a real input to (0,1) interval which might be interpreted as e.g. probability value. Right now - many experts advice not to use it because of it's saturation and non zero mean problems. You can read about it (as long as how to deal with the problem e.g. here http://jmlr.org/proceedings/papers/v9/glorot10a/glorot10a.pdf).
2. A sigmoid with softmax normalization is used to deal with two important problems which may occur during using of sigmoid function. First is dealing with outliers (it squashes your x to be around 0 and to make it sd = 1 what normalize your data) and second (and what is in my opinion more crucial) is to make different variables equally important in further analysis. To understand this phenomenon imagine that you have two variables age and income, where age varies from 20 to 70 and income varies from 2000 to 60000. Without normalizing data - both variables would be squashed to almost one by sigmoid transformation. Moreover - due to greater mean absolute value - income variable will be significantly more important for your analysis without any rational explaination.
3. I think that standarization is even more crucial in understanding softmax normalization than dealing with outliers. To understand why imagine a variable which is equal to 0 in 99% of cases and 1 in others. In this case your sd ~ 0.01, mean ~ 0and softmax normalization would outlie 1 even more.
4. Something completely different is a softmax function. A softmax function is a mathematical transformation from R^k to R^k which squashes a real valued vector to a positive valued vector of the same size which sums up to 1. It's given by an equation softmax(v) = exp(v)/sum(exp(v)). It's something completely different than softmax normalization and it's usually used in case of multiclass classification.

Torse