Solve the Heat Equation with non-zero Dirichlet BCs with Implicit Euler and Conjugate Gradient Linear Solvers?

Let's solve this problem in steps. First, let's build the linear operator for the discretized Heat Equation with Dirichlet BCs. A discussion of the discretization can be found on this Wiki page which shows that the central difference method gives a 2nd order discretization of the second derivative by (u[i-1] - 2u[i] + u[i+1])/dx^2. This is the same as multiplying by the Tridiagonal matrix of [1 -2 1]*(1/dx^2), so let's start by building this matrix:

using LinearAlgebra, OrdinaryDiffEq
x = collect(-π : 2π/511 : π)

## Dirichlet 0 BCs

u0 = @. -(x).^2 + π^2

n = length(x)
A = 1/(2π/511)^2 * Tridiagonal(ones(n-1),-2ones(n),ones(n-1))

Notice that we have implicitly simplified the end, since (u[0] - 2u[1] + u[2])/dx^2 = (- 2u[1] + u[2])/dx^2 when the left BC is zero, so the term is dropped from the matmul. We then use this discretization of the derivative to solve the Heat Equation:

function f(du,u,A,t)
    mul!(du,A,u)
end

prob = ODEProblem(f,u0,(0.0,10.0),A)
sol = solve(prob,ImplicitEuler())

using Plots
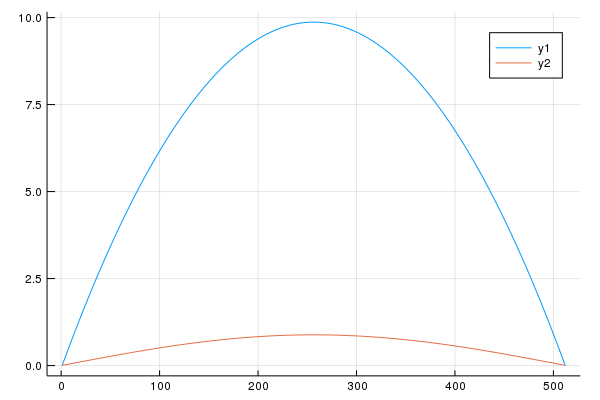
plot(sol[1])
plot!(sol[end])

Now we make the BCs non-zero. Notice that we just have to add back the u[0]/dx^2 that we previously dropped off, so we have:

## Dirichlet non-zero BCs
## Note that the operator is no longer linear
## To handle affine BCs, we add the dropped term

u0 = @. (x - 0.5).^2 + 1/12
n = length(x)
A = 1/(2π/511)^2 * Tridiagonal(ones(n-1),-2ones(n),ones(n-1))

function f(du,u,A,t)
    mul!(du,A,u)
    # Now do the affine part of the BCs
    du[1] += 1/(2π/511)^2 * u0[1]
    du[end] += 1/(2π/511)^2 * u0[end]
end

prob = ODEProblem(f,u0,(0.0,10.0),A)
sol = solve(prob,ImplicitEuler())

plot(sol[1])
plot!(sol[end])

Now let's swap out the linear solver. The documentation suggests that you should use LinSolveCG here, which looks like:

sol = solve(prob,ImplicitEuler(linsolve=LinSolveCG()))

There are some advantages to this, since it has a norm handling that helps conditioning. Howerver, the documentation also states that you can build your own linear solver routine. This is done by giving a Val{:init} dispatch that returns the type to use as the linear solver, so we do:

## Create a linear solver for CG
using IterativeSolvers

function linsolve!(::Type{Val{:init}},f,u0;kwargs...)
  function _linsolve!(x,A,b,update_matrix=false;kwargs...)
    cg!(x,A,b)
  end
end

sol = solve(prob,ImplicitEuler(linsolve=linsolve!))

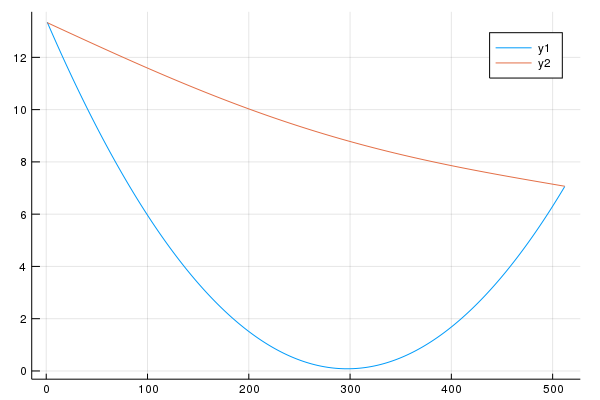
plot(sol[1])
plot!(sol[end])

And there we are, non-zero Dirichlet Heat Equation with a Krylov method (conjugate gradients) for the linear solver, making it a Newton-Krylov method.

Recommended topics

Hot tags