Eigenvectors are complex but only for large matrices

Question

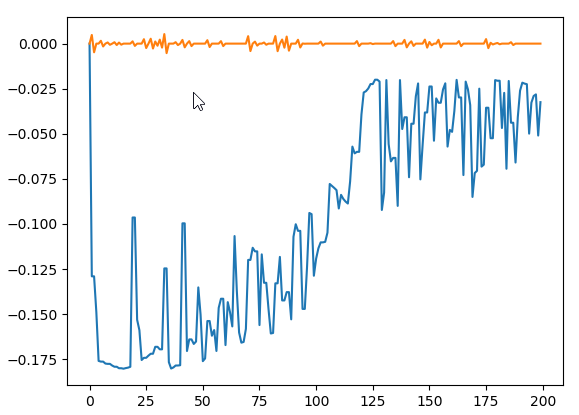
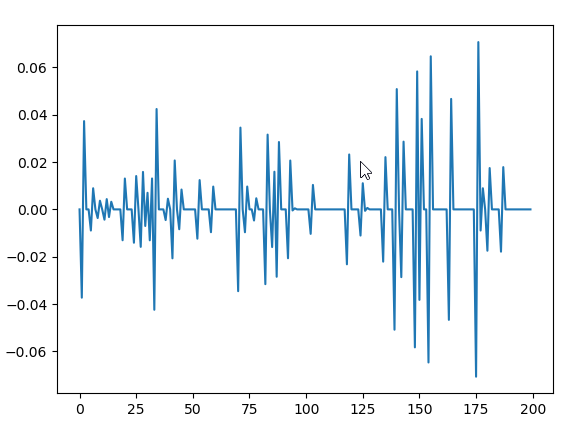
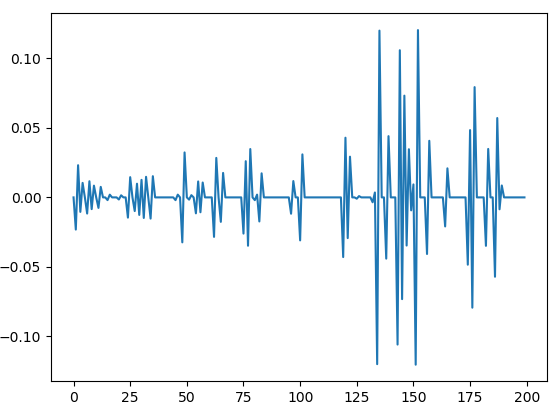
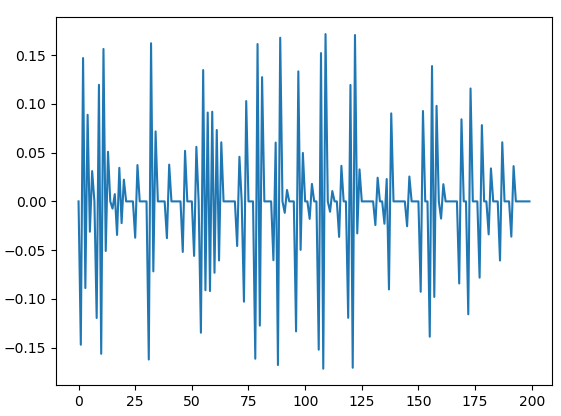
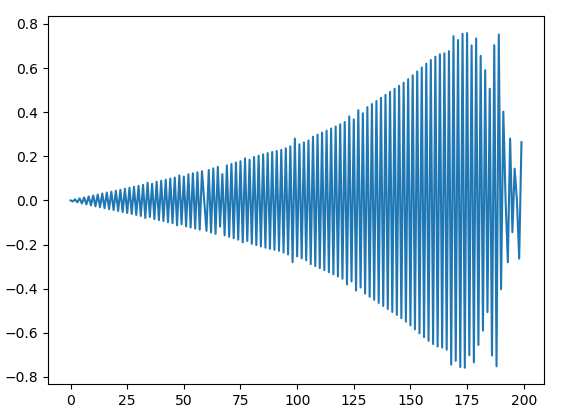
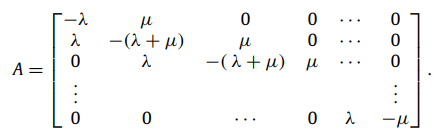I'm trying to calculate the eigenvectors and eigenvalues of this matrix

import numpy as np
la = 0.02
mi = 0.08
n = 500

d1 = np.full(n, -(la+mi), np.double)
d1[0] = -la
d1[-1] = -mi
d2 = np.full(n-1, la, np.double)
d3 = np.full(n-1, mi, np.double)

A = np.diagflat(d1) + np.diagflat(d2, -1) + np.diag(d3, 1)
e_values, e_vectors = np.linalg.eig(A)

If I set the dimensions of the matrix to n < 110 the output is fine. However, if I set it to n >= 110 both the eigenvalues and the eigenvector components become complex numbers with significant imaginary parts. Why does this happen? Is it supposed to happen? It is very strange behavior and frankly I'm kind of stuck.

Homograph

I'm not seeing a "significant" imaginary component here. It's mostly zero, with some values that are on the order of 1e-3 of their real part. That is likely ascribable to the roundoff error you get with such a large problem. – Grabble

Answer 1

What you are seeing appears to be fairly normal roundoff error. This is an unfortunate result of storing floating point numbers with a finite precision. It naturally gets relatively worse for large problems. Here is a plot of the real vs. imaginary components of the eigenvalues:

You can see that the imaginary numbers are effectively noise. This is not to say that they are not important. Here is a plot of the imaginary vs. real part, showing that the ratio can get as large as 0.06 in the worst case:

This ratio changes with respect to the absolute and relative quantities la and mi. If you multiply both by 10, you get

If you keep la = 0.02 and set mi = 0.8, you get a smaller imaginary part:

Things get really weird when you do the opposite, and increase la by a factor of 10, keeping mi as-is:

The relative precision of the calculation decreases for smaller eigenvalues, so this is not too surprising.

Given the relatively small magnitudes of the imaginary parts (at least for the important eigenvalues), you can either take the magnitude or the real part of the result since you know that all the eigenvalues are real.

Grabble